Умножение матрицы на число: Для того чтобы умножить матрицу на число, нужно каждый элемент матрицы умножить на данное число.
Транспонирование матрицы: Для того чтобы транспонировать матрицу, нужно ее строки записать в столбцы транспонированной матрицы.
Сумма (разность) матриц: (должны быть одинаковыми по размеру) Для того чтобы сложить матрицы, необходимо сложить их соответствующие элементы. Таким же подобным образом происходит вычитание:
Умножение матриц: (Чтобы матрицу 
можно было умножить на матрицу 
нужно, чтобы число столбцов матрицыравнялось числу строк матрицы.)
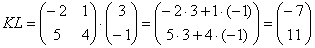1 2
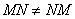
Нахождение обратное матрицы: (только для квадратных)
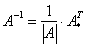
где 
– определитель матрицы 
, 
– транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .
Находим определитель матрицы: (если определитель равен 0 – обратной матрицы не существует.
Находим матрицу миноров
:
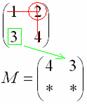
Находим матрицу алгебраических дополнений
: (меняем знаки)
Находим транспонированную матрицу алгебраических дополнений:
Используем формулу: Проверка: А*А^(-1)=Е(единичная матрица)
Свойства определителей:
· При транспонировании квадратной матрицы её определитель не меняется: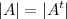 
· Общий множитель в строке можно выносить за знак определителя.
· 
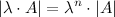То есть, если квадратная матрица 
-го порядка умножается на некоторое ненулевое число 
, то определитель полученной матрицы равен произведению определителя исходной матрицы 
на число в степени, равной порядку матриц.
· Если каждый элемент в какой-то строке определителя равен сумме двух слагаемых, то исходный определитель равен сумме двух определителей, в которых вместо этой строки стоят первые и вторые слагаемые соответственно, а остальные строки совпадают с исходным определителем.
· Если две строки определителя поменять местами, то определитель поменяет знак.
· Определитель с двумя равными строками равен нулю.
· Определитель с двумя пропорциональными строками равен нулю.
· Определитель, содержащий нулевую строку, равен нулю.
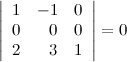
· Определитель не изменится, если к какой-то его строке прибавить другую строку, умноженную на некоторое число.
· Определитель верхней (нижней) треугольной матрицы равен произведению его диагональных элементов.
· Определитель произведения матриц равен произведению определителей: 
Билет №2 (2)
Точка и ее координаты 
на плоскости
Точка и ее координаты
в пространстве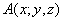 
;
Расстояние между двумя точками: (доказательство из Теоремы Пифагора)
Уравнение линии. Уравнением линии на плоскости в прямоугольной системе координат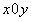 
называется уравнение 
, которому удовлетворяют координаты каждой точки данной линии и не удовлетворяют координаты любой точки плоскости, не лежащей на этой линии.
