1. Перед выполнением работы ознакомиться с основными определениями и формулами из раздела «Теоретическая часть».
2. Ознакомиться с заданием к лабораторной работе.
3. Нарисовать структурную схему САУ и проставить в блоках выражения для передаточных функций с численными значениями параметров типовых звеньев, взятыми из отчетных материалов лабораторной работы № 2.
4. Перед выполнением пунктов 1 и 2 задания запустить программу MATLAB и выполнить следующую последовательность действий:
1) Задать в окне команд описание передаточных функций разомкнутой (W (p)), а затем замкнутой (W з(p)) систем, используя при этом аналитическое выражение передаточной функции замкнутой САУ с пропорциональным звеном в цепи обратной связи, статический коэффициент усиления которого равен 1, 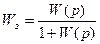 :
:
>> sys = (sys 1 + sys 2)* sys 3* sys 4.
>> sysz = sys *(1 + sys).
2) Набрать команду [>> step (sysz); grid ] для вывода переходной функции замкнутой САУ.
5. По графику переходной функции, пример которой показан на рис. 9, определить следующие показатели качества:
- время регулирования t p;
- перерегулирование Δ h max;
- частоту колебаний f к;
- число колебаний n;
- максимальную скорость v max изменения регулируемой величины.
Время регулирования t p определяет длительность переходного процесса и характеризует быстродействие системы. Теоретически переходной процесс длится бесконечно долго, однако он заканчивается практически, как только отклонение регулируемой величины от установившегося значения не будет превышать допустимых пределов ε = (3-5)%∙ h у. Иногда быстродействие системы характеризуют временем t у достижения переходной функцией первый раз установившегося значения или временем t max достижения максимального значения h max.
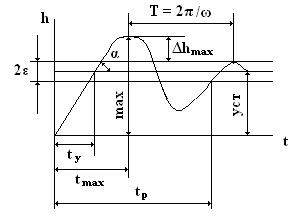
Рис. 9 Пример переходной характеристики колебательной системы
6. Набрать команду [>> bode (sysz); grid ] для вывода частотных функций ЛАЧХ и ЛФЧХ замкнутой САУ.
7. По графику ЛАЧХ (см. рис. 6) определить наклон кривой в области её пересечения с осью абсцисс в точке ωср и протяженность участка с данным наклоном. Если ωср = 20 дБ/дек, а протяженность участка средних частот приближенно равна одной декаде, то можно говорить об удовлетворительном приемлемом качестве регулирования.
8. По графику ЛАЧХ, если переходной процесс носит колебательный характер, определить значение ωmax.
10. Оформить отчет, который должен содержать:
- название и цель работы;
- основные определения, аналитические формулы и задаваемые команды;
- выводы с результатами оценки качества регулирования.
Приложение
АНАЛИЗ САУ С ПОМОЩЬЮ MATLAB и SIMULINK
По удобству графического пользовательского интерфейса, разнообразию моделей (блоков) в множестве библиотек, наличию виртуальных средств визуализации результатов моделирования SIMULINK выгодно отличается от множества программ аналогичного на значения. Возможности SIMULINK существенно усиливаются десятками пакетов расширения системы «MATLAB + SIMULINK».
Разработка моделей средствами SIMULINK основана на использовании мыши и технологии Drag-and-Drop («Перетащи и Оставь»). Для построения моделей САУ используются модули (или блоки), хранящиеся в библиотеке SIMULINK.
Блоки, включаемые в создаваемую модель, могут быть связаны между собой как по информации, так и по управлению. Характер связи зависит от типа блока и логики работы модели. Данные, которыми обмениваются блоки, могут быть скалярными величинами, векторами или матрицами произвольной размерности. Рассмотрим построение временных характеристик с помощью пакета Control System на примере апериодического звена первого порядка с передаточной функцией W (s) = 1/(0,5∙ s + 1). Необходимо сразу отметить, что в системе MATLAB для обозначения оператора Лапласа вместо символа р используется символ s.
В системе MATLAB для построения временных характеристик с помощью пакета используются функции step - для построения переходной функции h (t) и impulse - для построения весовой функции g (t).
Рассмотрим последовательность действий при этом:
1) в окне команд, которое высвечивается на экране монитора, с помощью клавиатуры задаем описание системы в виде передаточной функции W (s), используя при этом принятое в MATLAB ее сокращенное обозначение в виде tf (transfer function):
>> sys = tf ([1], [0.5 1]).
Параметрами функции tf являются вектора коэффициентов числителя и знаменателя передаточной функции W (s), заключенные в квадратные скобки, которые друг от друга должны быть разделены запятой. При этом значения коэффициентов обязательно отделяются друг от друга пробелами. Необходимо помнить, что при задании дробного числа вместо запятой следует ставить точку.
2) После набора функции нажимается клавиша Enter (ввод), в результате чего в окне команд отобразится набранная передаточная функция в обычном ее представлении:
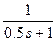 .
.
3) Задаем построение временных характеристик путем набора в окне команд соответствующих функций:
- для переходной характеристики: >> step(sys), после чего нажимаем клавишу Enter и на экране в отдельном окне высвечивается искомый график в следующем виде, рис. П.1
- для весовой (импульсной) характеристики: >> impulse(sys), в результате чего после нажатия клавиши Enter на экране появится график функции g (t), рис. П.2
Рассмотрим построение частотных характеристик САУ с помощью пакета Control System на примере нашего апериодического звена. Исходными данными для построения является рассмотренное выше описание системы, принятое в MATLAB, в виде передаточной функции:
>> sys = tf ([1], [0.5 1]).
Логарифмическая амплитудная (ЛАЧХ) и фазовая (ЛФЧХ) частотные характеристики задаются в Control System с помощью одной команды bode: >> bode (sys), после запуска которой с помощью нажатия клавиши Enter на экране появятся соответствующие графики, рис. П.3.
Диапазон частот для построения графиков выбирается по умолчанию автоматически. В случае, если выбранный диапазон не удовлетворяет постав
В качестве команды на построение годографа амплитудно-фазочастотной характеристики (АФЧХ) используется функция nyquist:
>> nyquist (sys)
Рассмотрим построение переходной характеристики для выбранного ранее в качестве примера апериодического звена с помощью программы SIMULINK, которую следует предварительно запустить, выбрав ее из верхней строки (меню) команд на экране монитора.
Для получения переходной характеристики САУ необходимо с помощью предоставляемого пользователю инструментария SIMULINK смоделировать поступление на вход системы сигнала в виде единичной ступенчатой функции, используя для этой цели блок единичного скачка Step, рис. П.4.
После подключения к выходу системы виртуального измерительного прибора в виде осциллографа (блока Scope) и последующего запуска процесса моделирования на экране монитора в отдельном окне получим соответствующий график переходной функции, рис. П.5.
При анализе параметров переходного процесса необходимо учитывать, что по умолчанию в блоке Step продолжительность скачка составляет не 0 с, а 1 с.
С помощью программы SIMULINK нельзя получить импульсную характеристику, так как в составе инструментария системы отсутствует блок, формирующий δ-функцию, а его моделирование путем дифференцирования единичного скачка дает большую погрешность.
Список литературы:
1. Теория автоматического управления/ Под ред. А.А. Воронова. Ч. 1 и 2. – М.: Высшая школа, 1986.
2. Ротач В.Я. Теория автоматического управления / Учебник для вузов.
– М.: МЭИ, 2006.






