МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное
учреждение высшего профессионального образования
"Казанский национальный исследовательский технический университет
Им. А. Н. Туполева-КАИ
(КНИТУ-КАИ)
НАБЕРЕЖНОЧЕЛНИНСКИЙ ФИЛИАЛ
Методические указания к выполнению
лабораторных работ
по дисциплине «Теория автоматического управления»
Набережные Челны
2011 г.
СОДЕРЖАНИЕ:
1. Лабораторная работа № 1. Исследование временных и частотных характеристик линейных САУ.
2. Лабораторная работа № 2. Исследование устойчивости линейных САУ.
3. Лабораторная работа № 3. Исследование показателей качества линейных САУ.
Приложение 1. Краткое руководство по применению MATLAB System и SIMULINK.
Список литературы
Лабораторная работа № 1
ИССЛЕДОВАНИЕ ВРЕМЕННЫХ И ЧАСТОТНЫХ ХАРАКТЕРИСТИК
ЛИНЕЙНЫХ САУ
Цель работы: изучение основных характеристик и параметров линейных систем автоматического управления (САУ).
Теоретическая часть
Линейной САУ называется динамическая система, поведение которой во времени описывается линейным дифференциальным уравнением n-степени:
a n∙ y (n) + a (n-1)∙ y (n-1) + … + a 1∙ y (1) + a 0∙ y = b m∙ x (m) + b (m-1)∙ x (m-1) + … + b 1∙ x (1) + b 0∙ x,
где a 0, b 0, …, a n, b n – постоянные коэффициенты уравнения;
y – регулируемая переменная (выходная функция САУ);
х – входная переменная (функция) САУ;
y (i) = di y (t) / d t i – i -я производная функции у, (i = 1, …, n);
x j = dj x (t) / d t j – j-я производная функции x (j = 1, …, m).
Так, например, подлежащие исследованию две линейные САУ описываются следующими дифференциальными уравнениями, соответственно, второй и третьей степени:
1) а 2∙ у (2) + а 1∙ у (1) = b 0∙ x;
2) a 3∙ y (3) + а 2∙ у (2) = b 0∙ x.
Представленные выше уравнения запишем в стандартной форме записи этих уравнений:
1) Т 22∙ у (2) + Т 1∙ у (1) = К ∙ x;
2) Т 33∙ y (3) + Т 22∙ у (2) = К ∙ x,
где К = b 0 – статический коэффициент усиления САУ;
Т 33 = а 3, Т 22 = а 2, Т 1 = а 1 – постоянные времени САУ, характеризующие ее динамические свойства.
Дифференциальные уравнения можно представить в операторной форме путем замены в них знака производной d/d t оператором Лапласа р:
1) Т 22∙ р 2∙ у + Т 1∙ р∙у = [(Т 2∙ р)2 + Т 1∙ р ]∙ у = К ∙ x;
2) Т 33∙ р 3∙ у + Т 22∙ р 2∙ у = [(Т 3∙ р)3 + (Т 2∙ р)2]∙ у = К ∙ x.
Отношение выходной величины у к входной переменной x в операторной форме есть передаточная функция W (p) САУ:
1) W (p) = y / x = К / [(Т 2∙ р)2 + Т 1∙ р ];
2) W (p) = y / x = К / [(Т 3∙ р)3 + (Т 2∙ р)2].
Для формализованного описания динамических свойств САУ наряду с дифференциальными уравнениями и передаточной функцией W (p)используются следующие способы:
временные функции, характеризующие изменение во времени выходного сигнала определенного вида;
частотные характеристики, устанавливающие зависимость между амплитудой и фазой входного и выходного гармонических сигналов при изменении частоты входного сигнала.
К временным характеристикам динамических звеньев относят переходную и весовую функции.
Переходная функция h (t) определяет характер изменения во времени выходного сигнала звена, если входной сигнал является единичной ступенчатой функцией x (t) = 1(t): y (t) = h (t)∙1(t) = h (t).
Весовая функция g (t) (импульсная переходная функция) определяет характер изменения во времени выходного сигнала звена, если входной сигнал является импульсной функцией x (t) = δ (t) = 1′(t), которая представляет собой производную от единичной ступенчатой функции, т.е. ее кривая на плоскости охватывает площадь, равную 1:
y (t) = g (t)∙ δ (t) = g (t)∙1′(t)
Весовая функция является производной от переходной функции. Следовательно, переходную функцию h (t) можно определить путем аналитического и графоаналитического интегрирования весовой функции g (t):
g (t) = d h (t)/d t; h (t) = ∫ g (t) ∙ d t.
Изображением весовой функции L [ g (t)], т.е. представлением ее в операторной форме, является передаточная функция W (p):
1) L [ g (t)] = W (p) = K / [(T 2∙ р)2 + Т 1∙ р ];
2) L [ g (t)] = W (p) = К / [(Т 3∙ р)3 + (Т 2∙ р)2].
С целью упрощения нахождения оригинала L -1[ W (p)] функции g (t), представленной в операторной форме, относительно сложное изображение W (p) можно разложить на сумму изображений более простых функций в виде элементарных дробей, воспользовавшись методом неопределенных коэффициентов:
1) 
;
2) 
.
Приведя правую часть полученных выражений к общему знаменателю, получим:
1) 
;
2) 
.
Так знаменатели левой и правой частей выражений равны, то, соответственно, равны и их числители, т.е.:
1) 
;
2) 
.
Приравняем коэффициенты при одинаковых степенях оператора Лапласа р левой и правой частей полученных формул:
1) К = А ∙ Т 1; 0 = А ∙ Т 22 + В;
2) К = В ∙ Т 22; 0 = А ∙ Т 22 + В ∙ Т 33; 0 = А ∙ Т 33 + С.
Решая систему уравнений (1) и (2), получим:
1) А = К / Т 1; В = - А ∙ Т 22 = - К ∙ Т 22 / Т 1;
2) В = К / Т 22; А = - В ∙ Т 33 / Т 22 = - К ∙ Т 33 / (Т 22)2;
С = - А ∙ Т 33 = К ∙(Т 33 / Т 22)2.
Подставляя значения коэффициентов А, В и С в соответствующие исходные формулы, получим:
1) 
=
= 
;
2) 
=
= 
= 
.
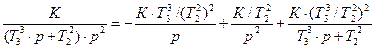Оригиналы изображений элементарных функций имеют следующий вид:
.
Заменяя в формулах 1) и 2) соответствующие изображения элементарных функций на их оригиналы, получим следующие выражения для весовых функций линейных САУ:
1) g (t) = 
; 2) g (t) = 
.
Так как переходная функция h (t) есть интеграл от весовой функции g (t), то найти ее можно либо путем непосредственного интегрирования функции g (t), либо путем нахождения сначала изображения L [ h (t)] функции h (t), а затем ее оригинала. Изображение переходной функции можно получить путем умножения передаточной функции (изображения L [ g (t)] весовой функции) на передаточную функцию идеального интегрирующего звена со статическим коэффициентом усиления, равным 1. Рассмотрим в качестве примера САУ с передаточной функцией W (p) = К / [(Т 2∙ р)2 + Т 1∙ р ]:
L [ h (t)] = W (p)∙ 
= 
.
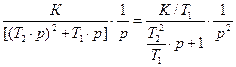Разложим полученное изображение передаточной функции на сумму изображений более простых функций в виде элементарных дробей, воспользовавшись методом неопределенных коэффициентов по аналогии с ранее рассмотренными примерами:
L [ h (t)] = 
= 
.
Найдем значения коэффициентов А, В и С:
.
Находим оригиналы элементарных функций:
L -1(1/ p) = 1; L -1(1/ p 2) = t; L -1[(T 1 / T 22) / (p + T 1 / T 22)] = [(T 1 / T 22)∙ 
.
Используя полученные выражения, находим оригинал искомой передаточной функции:
h (t) = 
+ 
+ 
∙ = 
.
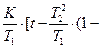
Частотные характеристики САУ характеризуют реакцию системы на синусоидальное входное воздействие в установившемся режиме.
К частотным характеристикам относятся:
АФЧХ - амплитудно-фазовая частотная характеристика;
АЧХ – амплитудно-частотная характеристика;
ФЧХ – фазовая частотная характеристика;
ЛАЧХ – логарифмическая АЧХ;
ЛФЧХ – логарифмическая ФЧХ.
АФЧХ представляет собой частотную передаточную функцию W (jω), которая получается путем замены в передаточной функции W (p) оператора Лапласа p на комплексную переменную jω. АФЧХ W (jω) можно представить в виде вектора на комплексной плоскости с координатами [ M (ω), N (ω)] или в полярных координатах Н(ω) и φ(ω), которые являются соответственно АЧХ и ФЧХ:
W (jω) = N (ω) + jM (ω) = Н (ω)∙ еjφ(ω ). (1)
Здесь: Н (ω) – АЧХ, которая представляет собой зависимость значения модуля вектора W (jω) от круговой частоты ω;
φ (ω) – ФЧХ, которая представляет собой зависимость аргумента вектора W (jω) от круговой частоты ω;
N (ω) = Н (ω)∙ cosφ (ω) – проекция вектора W (jω) на вещественную ось комплексной плоскости;
M (ω) = Н (ω)∙ sinφ (ω) – проекция вектора W (jω) на мнимую ось комплексной плоскости;
При изменении частоты ω от нуля до бесконечности конец вектора W (jω) вычерчивает кривую в комплексной плоскости, которая называется годографом АФЧХ.
Определим в качестве примера частотную передаточную функцию для САУ с передаточной функцией в операторной форме W (p) = К / [(Т 2∙ р)2 + Т 1∙ р ], которую для удобства дальнейших преобразований представим в виде:
W (p) = К / [(Т 2∙ р)2 + Т 1∙ р ] = К 1 / [(T∙p + 1)∙ p ],
где К 1 = К / Т 1; Т = (Т 2)2 / Т 1.
Произведя замену оператора Лапласа р на комплексную переменную jω, получим:
W (jω) = К 1 / [(jωT + 1)∙ jω ] = 
=
= 
. (2)
Из выражения (2) получаем формулы для нахождения модуля Н (ω) и аргумента φ (ω) вектора АФЧХ, а также его проекций на вещественную N (ω) и мнимую М (ω) оси:
Н (ω) = 
; φ (ω) = - [90o + arctg (ω∙T)];
N (ω) =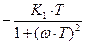 
; М (ω) = 
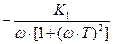. (3)
Фазовую частотную характеристику φ (ω) можно найти также из следующего соотношения: φ (ω) = arctg [ М (ω) / N (ω)] = -[180o - arctg (1/ ω∙T)].
Задание к лабораторной работе № 1
1. Используя метод неопределенных коэффициентов, найти аналитические выражения для весовой g (t) и переходной h (t) функций САУ, состоящей из двух последовательно соединенных элементарных динамических звеньев: апериодического и идеального интегрирующего звена.
2. Построить при помощи компьютерной программы MATLAB и вывести на печать графики найденных при выполнении п. 1 задания временных зависимостей g (t) и h (t).
3. Вывести аналитические выражения для частотных характеристик САУ по пункту 1: АФЧХ, АЧХ и ФЧХ.
4. Задаваясь характерными точками на оси частот построить примерные графики полученных при выполнении п. 3 задания частотных зависимостей.
5. При вычислениях следует использовать варианты параметров динамических звеньев, заданные табл. 1, в соответствии с последней цифрой шифра студента.
Примечание: тип 1 соответствует апериодическому звену;
тип 2 соответствует идеальному интегрирующему звену.
6. По результатам выполнения задания необходимо оформить отчет.
Таблица 1
| Тип звена | Параметры звена | Номер варианта | |||||||||
| К 1 | 0,5 | 0,2 | 0,1 | 0,4 | |||||||
| Т 1 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 0,05 | |
| К 2 | 0,8 | 0,4 | 0,5 | 0,5 |
Методические указания к выполнению лабораторной работы № 1
1. Перед выполнением работы ознакомиться с основными определениями и формулами из раздела «Теоретическая часть».
2. Ознакомиться с заданием к лабораторной работе и выполнить п. 1 задания, принимая во внимание, что при последовательном соединении звеньев передаточная функция САУ равна произведению их передаточных функций:
, где К = К 1∙ К 2, Т = Т 1.
3. Перед выполнением пункта 2 задания ознакомиться в Приложении с краткими сведениями по использованию базовой программы MATLAB, после чего запустить программу MATLAB и выполнить следующую последовательность действий:
1) задать в окне команд описание передаточной функции САУ W (p) с помощью функции tf (transfer function), параметрами которой являются вектора численных значений коэффициентов числителя и знаменателя передаточной функции. Например, описание передаточной функции W (p) = 10 / (2 ∙ p 2 + 0,5∙ p) будет выглядеть следующим образом: >> sys = tf ([10], [2 0.5 0]).
При нажатии клавиши Enter на экране монитора в окне команд высветится заданная передаточная функция в виде
,
где s – обозначение оператора Лапласа, принятое в МАТЛАБ.
Временную характеристику САУ g (t) строим с помощью функции impulse:
>> impulse (sys); grid,
где grid – признак отображения сетки графика.
При нажатии клавиши Enter на экране монитора в отдельном окне высветится график искомой весовой функции g (t) в виде, представленном на рис. 1.
Рис. 1 График весовой функции g (t) системы САУ,
описываемой передаточной функцией 
Скопировать с экрана график g (t), предварительно свернув все остальные открытые окна, и сохранить его как документ Word в папке «Мои документы» под произвольным именем.
Временная характеристика h (t) САУ строится с помощью функции step:
>> step (sys); grid.
После нажатия клавиши Enter на экране монитора в отдельном окне высветится график искомой переходной функции h (t) в виде, представленном на рис. 2.
Рис. 2 График переходной функции h (t) системы САУ,
описываемой передаточной функцией
Аналогичным образом скопировать с экрана график h (t), предварительно свернув все остальные открытые окна, и вставить его в свой документ Word.
4. Прежде, чем перейти к выполнению пункта 3 задания, необходимо также скопировать с экрана данные окна команд и вставить их в свой документ Word, а затем закрыть программу МАТЛАБ.
5. Выполнить пункты 3 и 4 задания, используя материалы раздела «Теоретическая часть».
6. Оформить отчет, который должен содержать:
- название и цель работы;
- основные определения и расчетные формулы;
- графики зависимостей g (t) и h (t) с отмеченными на них тремя значениями, рассчитанными предварительно по полученным формулам для значений времени t = T 1, 2 T 1 и 3 T 1;
- примерные графики частотных зависимостей с отмеченными на них двумя значениям, рассчитанными предварительно по полученным формулам для значений круговой частоты ω = 0 и 1 / Т 1;
- выводы.
Лабораторная работа № 2
