Цель работы: определение основных показателей качества регулирования САУ с использованием прямых и косвенных критериев.
Теоретическая часть
Наряду с обеспечением устойчивости САУ, как одного из основных показателей работоспособности системы, необходимо обеспечить требуемое качество переходного процесса при ступенчатых воздействиях, которое оценивают по переходной функции h (t), представляющей собой реакцию системы (у (t) = h (t)) на входное единичное воздействие (х (t) = 1(t)).
Основными показателями качества переходного процесса являются:
1. Время регулирования t p, которое представляет собой отрезок времени от момента появления единичного скачка входной величины до момента достижения регулируемой величиной уровня, равного 0,95 от установившегося значения h у = h (t → ∞), т.е. y (t p) = 0,95∙ h у.
2. Максимальное перерегулирование Δ h, которое представляет собой максимальное отклонение регулируемой величины относительно установившегося значения h у (Δ h = h max – h y), что характерно для затухающего колебательного процесса. Для оценки перерегулирования обычно используют относительную величину σ:
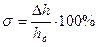 .
.
3. К оличество перерегулирований δ определяется количеством максимумов регулируемой величины, превышающих значение m, равное: m = 1,05∙ h у.
4. Частота колебаний f к регулируемой величины обратно пропорциональна интервалу времени Т к между соседними максимумами (периоду частоты): f к = 1/ Т к.
5. Число колебаний n определяется числом целых периодов Т к за время переходного процесса t п, окончание которого соответствует моменту времени, когда переходная функция h (t) входит в диапазон значений регулируемой величины 0,95∙ h у – 1,05∙ h у и далее при t ≥ t п из него не выходит, стремясь к значению h у.
6. Колебательность системы ξ оценивают, как отношение двух соседних максимумов: ξ = h (t 1 + Т к)/ h (t 1), где t 1 соответствует первому максимуму.
7. Максимальная скорость v max изменения регулируемой величины определяется графически как тангенс угла наклона переходной характеристики в точке первого пересечения с линией установившегося значения h у: v max = tg α = dh / dt.
8. Статическая погрешность εст замкнутой САУ в установившемся режиме есть разность между установившимися значениями сигналов на входе (x (t) = 1) и выходе (y (t) = h у): εст = 1- h у).
Наряду с переходной функцией h (t) для оценки качества переходного процесса широко применяются косвенные критерии, к которым относится частотная оценка.
Для указанной оценки используется относительная АЧХ в виде зависимости отношения H (ω)/ К от частоты ω: Δ(ω) = H (ω)/ К, рис. 8.
Относительная АЧХ на резонансной частоте ωmax имеет максимум, соответствующий значению Δ(ωmax) = Δmax. При дальнейшем увеличении частоты система вследствие своей инерционности не успевает реагировать на колебания больших частот и Δ(ω) резко «падает».
Установлено, что чем больше Δmax, тем более колебательным является переходной процесс. Отношение Δmax/Δ(0) = М называют показателем колебательности. Для статических САУ, не содержащих в своей передаточной функции множителя (1/р), Δ(0) = 1, поэтому М = Δmax. Обычно М = 1,2 – 1,5. При малых М система имеет большое время регулирования. При больших М увеличивается перерегулирование и система приближается к границе устойчивости.

Рис. 8 Относительная амплитудно-частотная характеристика САУ
Кроме частоты ωmax характерными частотами АЧХ являются частота среза ωс и полоса пропускания ωп. Частота среза замкнутой системы ωс определяется на уровне Δ(ω) = 1. Для статических САУ частота среза определяет диапазон вынужденных колебаний, которые система пропускает без ослабления. На этой частоте амплитуды входного и выходного колебаний равны. Полоса пропускания ωп замкнутой системы определяется на уровне Δ(0)/√2 = 0,707. Так как в диапазоне частот (ωс – ωп) АЧХ резко «падает», то числовые значения частот ωс и ωп близки.
Полоса пропускания влияет на точность и быстродействие системы. С увеличением полосы пропускания быстродействие системы растет. Чем больше полоса пропускания, тем больший спектр частот входного сигнала передается без искажений.
О качестве регулирования можно судить также по ЛАЧХ. Установлено, что для удовлетворительного качества регулирования участок средних частот, на котором ЛАЧХ пересекает ось абсцисс, должен имеет наклон минус 20 дБ/декаду. Протяженность этого участка влияет на перерегулирование. С его увеличением уменьшается колебательность переходного процесса. Приемлемое качество переходного процесса имеет место, если протяженность этого участка примерно равна декаде. Время регулирования t p зависит от частоты среза, при которой ЛАЧХ пересекает ось абсцисс. Чем больше частота среза, тем меньше t p.
Задание к лабораторной работе № 3
1. Для замкнутой линейной САУ (см. рис. 7), используя свои исходные данные из задания к лабораторной работе № 2, построить переходную характеристику h (t) и на ее основе определить основные показатели качества системы.
2. Для замкнутой линейной САУ (см. рис. 7), используя свои исходные данные из задания к лабораторной работе № 2, построить логарифмические частотные характеристики ЛАЧХ и ЛФЧХ и на их основе определить основные показатели качества системы.






