На рисунке 6 приведена стробоскопическая фотография движения материальной точки и указаны координатные оси.
Задание 1. Найти кинематический закон движения точки.
Спроецируем точки на координатные оси с учётом масштаба и выпишем в таблицу 1 значения координат точки, считая, что фотографирование началось при t = 0 и движение происходит по часовой стрелке. Измерения координат x и y прямые, поэтому оценим их погрешности по методике, изложенной в пункте б). Поскольку в данном случае нет особого смысла много раз измерять координаты, ибо мы будем получать всё время один и тот же результат, то следует предположить, что ∆хразбр. = ∆yразбр. = 0. Это не значит, конечно, что случайных ошибок нет – просто они меньше точности используемых инструментов. Приборная погрешность при измерении стандартной линейкой длиной 200 мм составляет ∆ хпр. = 0,2∙ 
=0,13 мм. Погрешность отсчёта и округления при округлении координат до 1 мм составит 0,5 мм. Следует учесть неидеальность процедуры проектирования, которая также приводит к погрешности отсчёта и округления и составляет примерно 0,5 мм (подумайте, почему!) результирующая погрешность будет равна по формуле (10):
(
Рисунок 6 – Стробоскопическая фотография движения материальной точки
Таблица 1
| t, cек | 0,10 | 0,20 | 0,30 | 0,40 | 0,50 | 0,60 | 0,70 | 0,80 | 0,90 | 1,0 | |
| x, см | 1,0 | 2,0 | 3,0 | 4,0 | 5,0 | 6,0 | 7,0 | 8,0 | 9,0 | 10,0 | 11,0 |
| y, см | 8,0 | 8,9 | 9,6 | 10,1 | 10,5 | 10,6 | 10,3 | 10,1 | 9,5 | 8,8 | 8,0 |
Для установления вида функциональной зависимости x = x(t) изобразим данные таблицы 1 на рисунке 7, откладывая время 
по горизонтали, координату x – по вертикали (в том же масштабе, что и на рисунке 6, руководствуясь при этом правилами, изложенными в пункте д).
При этом учитываем, что погрешность ∆t задана неявно (она равна 0,005 с). Из рисунка 7 сразу видно, что искомая функциональная зависимость x = x(t) линейная. Задача, следовательно, состоит в том, чтобы провести по точкам на рисунке 7 прямую, наилучшим в некотором смысле образом соответствующую этим точкам. Можно, конечно, это сделать графически, однако это не даёт полной уверенности, что прямая – наилучшая.
Рисунок 7 – Зависимость x = x(t)
Одним из способов аналитического решения задачи о нахождении наилучшей прямой, соответствующей экспериментальным точкам, является метод наименьших квадратов.
Идея метода состоит в следующем. Пусть уравнение искомой прямой имеет вид x = at + b, где a и b – постоянные, подлежащие определению. При каждом значении времени ti (0,1,…10) найдём величину(ati + b – xi)2, представляющую квадрат разности между экспериментальным значением величины xi и значением (ati + b), вычисленным по формуле, выражающей ожидаемую линейную зависимость. Образуем далее сумму 
. Прямая x = at + b будет соответствовать экспериментальным точкам наилучшим образом, если мы найдём такие значения a и b, при которых достигается минимум суммы S. Условия минимума имеют вид 
, 
, что даёт систему уравнений:
и 
Система, может быть переписана в виде:
Подставляя численные значения и решая систему, получим a = 10,0 см/с,
b = 1,0 см, так что искомая зависимость x(t) имеет вид
(37)
Существуют формулы, позволяющие определить погрешности значений a и b, однако мы их приводить не будем, а воспользуемся приближённым методом: относительная погрешность измерения координаты 
больше всего для наименьшего значения xmin = 1,0 см и составляет 10% и меньше всего для максимального значения xmax = 11,0 см (примерно 1%). Поэтому значения , вычисляемые по формуле (36) должны получаться с такой же относительной погрешностью. Именно поэтому мы имеем a = (10,0 
0,5) см/с, b = (1,00 0,05) см. Приводим на рисунке 7 наилучшую прямую.
Для нахождения вида функциональной зависимости y = y(t) поступим аналогично, изобразив данные из таблицы 1 на координатной плоскости (y,t) (рис. 8).
Рисунок 8 – Зависимость y = y(t)
Из рисунка 8 не вытекает, однако, с определённостью предположение о виде зависимости y = y(t). В таких случаях обычно выдвигаются гипотезы о том, какому классу функций (полиномов, показательных, тригонометрических и т. д.) принадлежит искомая зависимость, а затем эти гипотезы принимаются или отвергаются. Чаще всего выдвигается гипотеза о принадлежности неизвестной функции y(t) к классу полиномов некоторой степени n: 
. Степень 
полинома обычно берется вначале минимальной, совместимой с характером расположения экспериментальных точек. Из рисунка 8 сразу видно, что зависимость y(t) нелинейная, то есть n ≠ 1. Таким образом, мы берём функцию y(t) = aоt2 + a1t + a2 и ищем значения параметров aо, a1, a2, при которых эта функция наилучшим образом соответствует экспериментальным точкам рисунка 8. Задача решается на основе метода наименьших квадратов. Условия минимума суммы:
дают: 
Подставляя численные значения и решая систему уравнений, находим после округления aо = 10,0; a1 = 10,0; a2 = 8,0 (количество значащих цифр, в значениях a выбрано исходя из того, что относительная погрешность в определении координаты 
составляет примерно 1%). Таким образом, зависимость координаты
y = y(t) имеет вид
y = -10 t2 + 10 t + 8,0 (см) (38)
На рисунке 8 построена кривая (парабола), соответсвующая уравнению (38). Как видно, кривая достаточно хорошо проходит через экспериментальные точки. Следует, однако, помнить, что предположение о полиноминальной зависимости y = y(t) является лишь гипотезой. Ведь вполне возможно, что функция вида y = abt + c, где постоянные подобраны с помощью метода наименьших квадратов, или полином степени большей 2 значительно лучше соответствуют экспериментальным точкам рисунка 8. Иными словами, возникает вопрос, насколько оправдана гипотеза о полиноминальной зависимости степени 2, то есть насколько функция (38) соответствует экспериментальным точкам.
На первый взгляд, естественным представляется следующий путь. С помощью метода наименьших квадратов определим значения a, b, c для функции вида y = abt + c, при которых она наилучшим образом соответствует экспериментальным точкам, затем для этих значений a, b, 
вычислим сумму квадратов разностей, фигурирующих в методе наименьших квадратов, и сравним её с суммой для полиноминальной зависимости (38). Естетственнно, что та зависимость, для которой эта сумма меньше, лучше отвечает экспериментальным точкам. Ясно, однако, что этот путь, хотя и возможен, но трудоёмок и малоперспективен, поскольку существует множество функций времени, которые могли бы, в принципе, соответствовать экспериментальным точкам рисунка 6. Например, зависимость y = A sin (Bt + C) + D с надлежаще подобранными константами A, B, C, D. Поэтому вопросы совместимости гипотезы о той или иной зависимости (в нашем случае зависимости 38) с экспериментальными данными решаются с помощью так называемых критериев согласия (другое название – критерии значимости). Одним из наиболее удобных критериев является так называемый «критерий χ2» (читается хи-квадрат) или критерий Пирсона. В методе наименьших квадратов вычисляется величина χ2:
, (38)
то есть сумма квадратов отклонений экспериментальных значений yi от вычисленных по формуле (38), деленная на квадрат погрешности измерения величины y. В нашем случае χ2 = 3. Найденное значение χ2 должно быть сопоставлено с теорией. Это делается с помощью таблицы распределения χ2, фрагмент которой приведён в таблице 2. В данной таблице n – это число степеней свободы распределения χ2, равной числу измерений минус увеличенное на единицу число параметров, определяемых из эксперимента. В нашем случае число измерений равно 11 и с помощью метода наименьших квадратов было определено 3 параметра, так что n = 11 – (3 + 1) = 7. Число Р в таблице – вероятность, выражаемая в процентах. По найденному значению χ2 = 1,3 и числу степеней свободы n = 7 находим, что P ≈ 98%. Это означает, что если гипотеза о зависимости (38) справедлива, то найденное или большее значение χ2 должно встречаться примерно в 98% случаев. Следовательно, на уровне доверительной вероятности 98% мы подтвердили зависимость (38). Если, например, при тех же условиях
χ2 = 14,1, то это означало бы, что при справедливости гипотезы (38) такие большие отклонения встречались бы лишь в 5% случаев, так что наше найденное значение χ2 = 14,1 свидетельствовало бы о ненадёжности гипотезы, и это заставило бы искать другую зависимость y(t), например, в виде полинома третьей степени и т. д.
Выпишем окончательно найденный кинематический закон движения:
x = 10,0 t + 1,0 (см) (39)
y = -10 t2 + 10 t + 8,0 (см)
На рис. 8 построена кривая (парабола), соответствующая уравнению (38). Как видно, кривая достаточно хорошо проходит через экспериментальные точки.
Задание 2. Найти среднюю скорость частицы в интервале времениt (0,4;0,8),её модуль и углы с осями координат.
Имеем: x (0,4) = 5,0 см; x (0,8) = 9,0 см y (0,4) = 10,4 см; y (0,8) = 9,6 см
Тогда ∆ x = 4,0 см, ∆ y = – 0,8 см, ∆ t = 0,4 с
; 
; 
; 
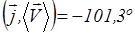
Обратите внимание, что для того, чтобы получить правильное значение для 
, нужно вычислить значение модуля средней скорости более точно, чем записано выше: 
Задание 3. Найти модуль мгновенной скорости в момент t 1 = 0,7 сек и углы с осями координат.
; 
; 
; 
Задание 4. Найти ускорение частиц в тот же момент и углы, составляемые вектором ускорения с осями координат.
; 
, 
; 
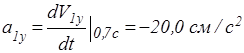
Вектор скорости и ускорения изображены на рисунке 5.
Задание 5. Найти тангенциальное и нормальное ускорения в тот же момент времени.
Направлен вектор 
так же, как и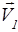 
. Изображаем его на рисунке. Вектор 
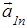может быть найден геометрически: 
. Этот вектор также показан на рисунке 6.
Задание 6. Найти радиус кривизны траектории в точке, соответствующей тому же моменту времени.
Используя формулу (34), находим: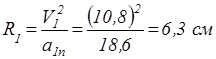 
Во многих случаях оказывается полезным приближенный графический способ нахождения радиуса кривизны. Для этого точку на траектории, соответствующего моменту времени t1 = 0,70 c,соединим прямолинейными отрезками с соседними точками, соответсвующими моментам t2 = 0,60 c и t3 = 0,80 c. Из середины этих отрезков восстанавливаем перпендикуляр до их перечисления в точке 0.
Точка 0 примерно совпадает с центром соприкасающейся окружности, соответствующей участку траектории вблизи точки, для которой велось построение. Радиус окружности примерно равен R 1.
Задание 7. Найти зависимость пройденного пути S от времени t, то есть функцию S = S(t).
Имеем: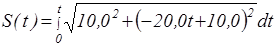 
Проведите вычисление самостоятельно, используя табличный интеграл
Получим: 
Задание 8. Написать уравнение траектории точки.
Исключая время t из уравнений (39), имеем:
Или y = – 0,1x2 + 1,2x + 6,9 (см). Это и есть уравнение траектории.
Задание 9. Найти скорость удаления частицы от начала координат в момент времени t1 = 0,7 c.
Расстояние от частицы до начала координат согласно формуле (39) равно:
Поэтому: 
(См. формулу 36 стр.15)
Теперь достаточно подставить значение t1 = 0,7 c.
Задание 10. Найти относительную скорость двух частиц в момент времени
t1 = 0,7 c.
Допустим, что спустя время tо = 0,2 c из той же начальной точки с той же начальной скоростью по той же траектории движется другая частица. Требуется найти относительную скорость частиц в момент t1 = 0,7 c. Скорость второй частицы в момент t1 = 0,7 c будет такая же, как скорость первой в момент 0,5 с. Поэтому, так же, как и в задании 3, можно определить скорость частицы в момент 0,5 с.
, 
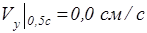
Тогда Vотнх = 0,0 см/с, Vотну = – 4,0 см/с и скорость первой частицы относительно второй частицы в момент времени 0,7 секунд равна 4 см/с и направлена вниз.
Стробоскопические фотографии для выполнения работы каждый студент получает у преподавателя.
Контрольные вопросы.
1. Какие ошибки (пункт а)) имели место при выполнении работы и как они учитывались?
2. Как изменилась бы точность ваших результатов, если бы вы проводили все измерения и построения несколько раз, используя разные инструменты?
3. Как можно проверить отсутствие промахов в серии наблюдений?
4. Изложите методику расчёта погрешностей при измерении объёма цилиндра штангенциркулем.
5. Нарисуйте, примерно, как будет выглядеть стробоскопическая фотография движения точки при 
и 
.
6. Запишите выражение для векторов скорости и нормального ускорения 
в указанный преподавателем момент времени и проверьте выполнение условий 
.
7. Нанесите экспериментальные точки и постройте теоретическую кривую зависимости от времени той координаты, для которой она нелинейная, откладывая вдоль оси абсцисс значения 
, а вдоль оси ординат – значения этой координаты. Сделайте выводы.
Таблица 2 χ2 распеделения
| N/P% | ||||||||
| 0,8 | 0.7 | 1,1 | 1,6 | 2,2 | 3,4 | 6,0 | 9,5 | |
| 0,6 | 1,1 | 1,6 | 2,3 | 3,0 | 4,4 | 7,3 | 11,1 | |
| 0,9 | 1,6 | 2,2 | 3,1 | 3,8 | 5,3 | 8,6 | 12,6 | |
| 1,3 | 2,2 | 2,8 | 3,8 | 4,7 | 6,3 | 9,8 | 14,1 | |
| 1,6 | 2,7 | 3,5 | 4,6 | 5,5 | 7,3 | 11,0 | 15,5 | |
| 2,1 | 3,3 | 4,2 | 5,4 | 6,4 | 8,3 | 12,2 | 16,9 | |
| 2,6 | 3,9 | 4,9 | 6,2 | 7,3 | 9,3 | 13,4 | 18,3 | |
| 3,1 | 4,6 | 5,6 | 7,0 | 8,3 | 10,3 | 14,6 | 19,7 | |
| 3,6 | 5,2 | 6,3 | 7,8 | 9,0 | 11.3 | 15,8 | 21,0 | |
| 4,1 | 5,9 | 7,0 | 8,6 | 9,9 | 12,3 | 17,0 | 22,4 |
