Вагон или локомотив опираются на колеса через листовые рессоры или пружины. Поэтому колеса воспринимают ударные воздействия от рельсов непосредственно, а кузов вагона – через пружины подвески. Кратковременная вертикальная сила удара на колесо вагона со стороны рельса возникает при прохождении колесом стыка между рельсами, при накате ползуна (лыски) на рельс, а также при качении колеса с большой скоростью по неровному профилю пути. Воздействие стыков рельсов на колесо связано с тем, что в месте соединения соседних рельсов накладкой жесткость рельсовой пути меньше, чем в середине рельса. Поэтому в месте стыка рельсы изгибаются, и колесо при движении падает с рельса на следующий рельс (рис. 15.3). Расстояние между точками удара больше ширины стыка.
Оценим силовое воздействие стыка рельсов или ползуна на колесо. На колесо опирается часть вагона с массой M, много большей массы колеса. За краткое время удара подрессоренный вагон практически не сместится в вертикальном направлении, поэтому удар воспринимает только колесо некоторой массой m. Колесо при прохождении стыка вращается вокруг мгновенной оси, проходящей через контакт А, и падает в стык. В точке В происходит удар колеса о рельс и возникает ударная сила реакции N, направленная почти вертикально. В это мгновение в точке А колесо уже отрывается от рельса. Скорость колеса при ударе изменяет направление от VA до VB, а колесо получает вертикальную компоненту скорости Δ V. На рисунке угол α сильно преувеличен, поэтому приращение скорости можно определить из треугольника скоростей: Δ V=αV, а из треугольника расстояний: 
. Тогда вертикальная составляющая скорости колеса после удара будет равна 
.
Согласно второму закону Ньютона изменение импульса колеса при ударе равно импульсу силы удара: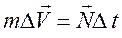 
. Откуда импульс силы можно определить по формуле
. (15.8)
Здесь N –– средняя сила удара, R –– радиус колеса, b –– ширина стыка с учетом изгиба рельсов или длина ползуна, Δ t –– время процесса удара.
Рассмотрим воздействие колеса, получившего вертикальную скорость, через пружину подвески на вагон. После удара пружина начинает сжиматься. По мере сжатия сила давления пружины на вагон возрастает. Достигнув максимальной степени сжатия, пружина начнет распрямляться, прижимая колесо к рельсу и поднимая вагон. Если считать, что масса вагона намного больше массы колеса, то колесо колеблется относительно вагона, как пружинный маятник с периодом 
. Колебательное движение колеса относительно вагона происходит по закону синуса. Пропорционально смещению изменяется сила давления пружин подвески на вагон 
.
По закону сохранения импульса для процесса взаимодействия колеса и вагона импульс колеса и равный ему импульс ударной силы получит вагон. На графике «сила – время», (рис. 15.4) импульс силы удара равен площади узкого почти треугольника, тогда как импульс силы давления пружины на вагон равен площади под графиком синусоиды за половину периода. Площадь определяется интегралом
. (15.9)
Отсюда амплитуда силы давления пружины на вагон равна
.(15.10)
Как видно, чем больше период колебаний колеса относительно вагона, то есть чем мягче пружины подвески, тем меньше сила воздействие толчков колес на вагон.
Определим энергию, передаваемую вагону. Кинетические энергии запишем как отношение квадрата импульса к двойной массе тел: 
. Так как импульсы вагона и колеса равны, 
, то энергия, переданная вагону, будет меньше энергии колеса. Их отношение равно отношению масс:
. (15.11)
Остальная, большая часть энергия удара, теряется в амортизаторах, рессорах при затухающих колебаниях вагона и колеса и, в конце концов, переходит в теплоту. Итак, назначение рессор состоит в том, чтобы уменьшить силы удара на вагон от колес, растянуть время воздействия, уменьшить энергию удара, передаваемую вагону, и тем самым повысить комфортность для пассажиров и грузов. Для этого масса неподрессоренного колеса должна быть как можно меньше по сравнению с надрессорной массой вагона, но не в ущерб прочности. Следует уменьшать параметр 
, используя более жесткий рельсовый путь, бесстыковые рельсы и не применять колес с ползунами.
Задачи
1. Амплитуда вертикальных колебаний вагона массой 60 т за три секунды уменьшилась в два раза. Определить коэффициент сопротивления амортизаторов.
2. Амплитуда вертикальных колебаний вагона массой 60 т за три колебания уменьшилась в 2,72 раза. Определить коэффициент сопротивления амортизаторов, если коэффициент упругости пружин подвески 2·107 Н/м.
3. Определить импульс силы удара и силу удара, полученного колесом при накатывании ползуна длиной 16 мм на рельс со скоростью 20 м/с. Диаметр колеса 1,02 м, масса колеса 800 кг. Во сколько раз сила действия пружины подвески на вагон меньше силы удара стыка рельсов на колесо, если период колебаний колеса относительно вагона 0,2 с.
4. Определить амплитуду силы давления пружины подвески на вагон, если колесо массой 800 кг и со скоростью 20 м/с наезжает на стык рельса с ударом. Отношение ширины стыка к радиусу колеса 1/50. Период собственных колебаний колеса относительно вагона 0,2 с.
5. Определить, при каком минимальном значении коэффициента сопротивления амортизаторов вагона массой 40 т, вагон после смещения внешним воздействием без колебаний стремится к положению равновесия (апериодическое колебание).
6. Время релаксации колебаний вагона 3 с. Определить относительные потери энергии за одно колебание. Масса вагона 40 т, коэффициент упругости пружин подвески 2·107 Н/м.
7. Вертикальные колебания вагона массой 40 т происходят по закону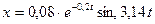 
. Определить коэффициент упругости рессор вагона, через сколько колебаний энергия колебаний уменьшится в 10 раз.
16. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
