Галопирующие колебания – это вращательные колебания вокруг горизонтальной оси Y, перпендикулярной бортам вагона и проходящей через центр масс вагона. При этом движение вагона подобно галопу лошади. Колебания обусловлены упругими силами подвески и инертностью вагона.
Пусть из-за случайного толчка, например на стыке рельсов или при падении груза, корпус вагона наклонился. Пусть при этом пружины передней вагонной тележки сжались, а задней тележки – растянулись. Возникает момент упругих сил пружин подвески, стремящийся вернуть вагон в положение равновесия. Но вагон по инерции проходит положение равновесия, поворачиваясь в противоположном направлении. Потом движение повторяется в обратном направлении, и таким образом возникают галопирующие колебания.
Определим период галопирующих колебаний. Так как это вращательные колебания, то для вывода применим основной закон динамики вращательного движения: произведение момента инерции вагона относительно оси вращения на угловое ускорение равно моменту упругих сил подвески: J ε = М.
Получим формулу для момента силы, который создают пружины подвески. По закону Гука упругие силы пружин пропорциональны деформации пружин и направлены противоположно деформации F = –kx. Так как передняя подвеска сжата, то ее сила упругости направлена вертикально вверх, а сила упругости растянутой задней подвески – вниз (рис. 14.5). Момент пары упругих сил подвески F равен произведению силы на плечо пары сил: M = F l, где плечо l равно расстоянию между линиями действия сил, то есть между серединами передней и задней вагонных тележек. Деформация пружин х связана с
 |
углом поворота вагона как длина дуги с центральным углом:
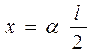. Итак, момент упругих сил равен 
.Подставив в закон динамики формулу момента силы, получим дифференциальное уравнение галопирующих колебаний
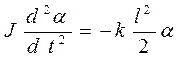. (14.14)
Здесь угловое ускорение записано как вторая производная от угла поворота по времени. Решением этого дифференциального уравнения должна быть функция, у которой вторая производная имеет такой же вид, как и сама функция, но противоположного знака. Например, это может быть функция косинуса
α= α 0cos ω t, (14.15)
где α 0– амплитуда колебаний, ω – циклическая частота колебаний. Если определить вторую производную от угла поворота по времени 
и подставить в дифференциальное уравнение, то выбранная функция будет решением, при условии, если циклическая частота колебаний равна 
. Период колебаний 
будет равен
. (14.16)
Здесь k –– коэффициент упругости пружин подвески, принятый одинаковым для передней и задней вагонных тележек, J – момент инерции вагона.
Задачи
1. Определить период колебаний железнодорожной платформы массой 20 т относительно горизонтальной оси, если платформа одним краем висит на упоре. Коэффициент упругости подвески 1·107 Н/м
2. Определить период галопирующих колебаний двухосного вагона массой 40 т, если расстояние между осями 10 м. Коэффициент упругости одной пружины 2·107 Н/м, длина вагона 15 м.
3. Тяговый двигатель при опорно-осевом подвешивании с моментом инерции 50 кг м2 подвешен к раме вагона на пружине, коэффициент упругости которой 2·105 Н/м. Определить частоту собственных колебаний двигателя, если расстояние от оси до пружины 0,4 м.
4. При подвешивании тягового двигателя массой 500 кг к раме вагона пружины подвески растянулись на 0,5 см. Определить период колебаний двигателя.
5. На платформу массой 20 т опустился контейнер массой 5 т со скоростью 1м/с. Определить амплитуду и период вертикальных колебаний платформы. Коэффициент упругости пружин подвески 1·10 7 Н/м.
6. Платформа массой 40 т при движении совершает вертикальные колебания с частотой 2 Гц и амплитудой 1 см. Определить наибольшую скорость и ускорение колебаний платформы. Определить наибольшую и наименьшую силы давления вагона на рельсы.
7. Определить амплитуду и период горизонтальных колебаний вагона массой 60 т на пружине автосцепки, если вагон на скорости 0,5 м/с сцепился с таким же вагоном. Коэффициент упругости пружин автосцепки 2·105 Н/м. Трением пренебречь.
15. ЗАТУХАЮЩИЕ КОЛЕБАНИЯ
Затухающие колебания – это собственные колебания маятников, амплитуда которых со временем уменьшается. Реально собственные колебания всегда затухающие из-за действия силы сопротивления среды.
