Лабораторная работа № 191. Исследование упругого и пластичного удлинения проволки
Введение
Все реальные тела под воздействием сил в той или иной степени меняют свою форму, деформируются.
Абсолютно упругое тело является самой простой моделью, в рамках которой учитывается возможность деформации (изменения формы) реальных тел.
 Рис.1
Рис.1
|
Все разнообразие деформаций сводится к двум основным типам, которые можно назвать элементарными. Этими элементарными деформациями являются растяжение (и сжатие) и сдвиг. Наглядно представить эти деформации помогает рисунок 1. Здесь показано сечение параллелепипеда, жестко закрепленного на массивном жестком столе. Пусть внешняя сила равномерно распределена по верхней грани параллелепипеда. При этом, очевидно, такая же по величине, но обратная по направлению сила действует на параллелепипед со стороны стола. Существует два независимых направления силы по отношению к грани, к которой эта сила приложена: нормальное (на рисунке слева) и тангенциальное (на рисунке справа).
В первом случае действие силы приводит к сжатию образца, если сила направлена внутрь тела, и к растяжению в противном случае. Количественной характеристикой растяжения (сжатия) является относительное удлинение
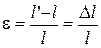 . (1)
. (1)
где l - длина параллелепипеда до приложения нагрузки, l' - во время действия внешней силы. При растяжении e>0, при сжатии e<0. Величину D l называют удлинением образца.
Во втором случае (см. рисунок 1 справа) действие силы приводит к смещению слоев тела параллельно друг другу вдоль направления действия силы. Сдвиг характеризуется тангенсом угла g. При малых деформациях этот сдвиг мал и можно полагать tgg = g.
 Рис.2.
Рис.2.
|
Исследование деформаций тел сводится к установлению зависимости e и g от приложенной нагрузки. В качестве меры последней выбирается величина f отношения приложенной внешней силы F к площади грани S, на которую эта сила непосредственно действует: f = F / S. Характерные результаты экспериментов по растяжению-сжатию образцов представлены на рисунке 2. Участок кривой АB соответствует так называемым упругим деформациям. Особенность их в том, что при снятии нагрузки меньшей fA (при растяжении) или fB (при сжатии) деформации исчезают. Если внешняя сила превысит предел упругости fA (fB) деформации станут неупругими. Т.е. при снятии нагрузки всегда будет иметь место некоторая остаточная деформация. Легко сообразить, что в области неупругих деформаций, нет однозначной зависимости между величиной приложенной нагрузки и величиной деформации. Такую ситуацию весьма затруднительно описать теоретически.
Для упруго деформированного тела согласно закону Гука имеет место однозначная зависимость между приложенной нагрузкой и возникающей деформацией, которая в случае малых деформаций линейна:
f n = E e, f t = G g1. (2)
где E - модуль Юнга (модуль растяжения), G - модуль сдвига.
Модель абсолютно упругого тела предполагает, что подобная линейная зависимость имеет место при любой деформации.
Приступая к работе необходимо
Знать определения
удлинения и относительного удлинения;
упругой и пластической деформации;
упругого напряжения;
модуля Юнга.
Знать
формулировку и границы применения закона Гука;
Уметь
запускать программы в среде Windows и пользоваться стандартными элементами их интерфейса (меню, контекстные меню, окна и т.д.);
оценивать случайные погрешности прямых и косвенных измерений.
Цель работы
исследование деформаций металлических проволок.
Решаемые задачи
ü наблюдение упругого гистерезиса;
ü экспериментальная проверка закона Гука;
ü экспериментальное определение предела упругости;
ü измерение модуля Юнга.
Экспериментальная установка
Приборы и принадлежности:
ü исследуемые проволоки;
ü датчик силы;
ü датчик угла поворота;
ü микровинт;
ü система крепления;
ü компьютерный интерфейс сенсор-CASSY Lab 2;
ü компьютер.
Порядок выполнения работы
1. Поскольку приходится работать одновременно двумя руками, правшам удобнее разместить компьютер слева от датчика угла, левшам – справа.
2. Подключите интерфейс CASSY Lab 2 и компьютер к электрической сети 220 В, войдите в систему Windows;
3. С рабочего стола Windows стартуйте иконку с названием работы.
4. На переднем плане возникнет окно с именем “CASSYs”. Щелкните в нем кнопку “Show measuring parameters” - в правой части основного окна программы появится окно “Settings”. Закройте окно “CASSYs”.
5. В окне “Settings” последовательно откройте ветви дерева “Sensor-CASSY 2” – “Force”. Щелкните по ней мышкой. Справа внизу появится окно “ ” для управления режимом регистрации силы.
6. Привяжите концы проволоки к датчику силы и колесу датчика угла как показано на рис.2
 Рис. 2а
Рис. 2а
 Рис. 2б
Рис. 2б
|
7. Измерьте микрометром толщину проволоки d. Считая её поперечное сечение кругом, рассчитайте его площадь S = p d 2/4.
8. Измерьте рулеткой расстояние l между точкой соприкосновения с диском датчика силы и местом крепления проволоки к датчику силы.
9. Измерьте штангенциркулем рабочий диаметр колеса датчика угла.
10. Внесите данные измерений в соответствующие поля в окне программы.
11. Плавно поворачивая колесо датчика силы основной рукой, слегка натяните проволоку.
12. Удерживая колесо в таком состоянии, обнулите показания датчика силы. Для этого в окне “Settings”щёлкните мышкой по ветке “Force” и в открывшемся снизу окне настроек датчика силы щёлкните кнопку “>0<”.
13. Аналогично п 11, обнулите показания датчика угла.
14. Нажмите клавишу F9 для запуска автоматической регистрации данных.
15. Плавно вращая колесо датчика силы постепенно растяните проволоку примерно на 3-4 мм. При этом на экране компьютера должен отображаться график зависимости f (e).
16. Ослабьте усилие руки, вращающей колесо. Обратите внимание, что график вернулся в исходную точку.
17. Плавно вращая колесо датчика силы постепенно растягивайте проволоку вплоть до её разрыва. Нажмите F9 для завершения регистрации данных.
18. Повторите действия 6-17 для проволоки из другого материала.
Обработка и представление результатов
Для исследованных проволок нАайдите пределы упругости, модули Юнга, предельные натяжения, сравните области пластической деформации. Сделайте вывод о возможности использования материалов проволок в механических устройствах.
Лабораторная работа № 192. Проверка закона дисперсии звуковых волн в воздухе
Введение
Фазовая скорость волны является характеристикой среды, в которой имеет место волновое движение.
Например, для звуковых волн в воздухе имеет место соотношение:
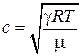 , (1)
, (1)
где R - универсальная газовая постоянная, T - температура, m - молярная масса g - показатель адиабаты воздуха. Это соотношение обычно используется для определения температурной зависимости g.
В курсе механики интерес представляет само по себе измерение фазовой скорости звука, в частности, закона дисперсии – зависимости фазовой скорости волны от частоты n.
Измерить c можно пользуясь следующими соображениями. Расстояние между двумя пучностями стоячей звуковой волны равно половине длины волны. Длина волны λ задается расстоянием d между первой и n-й пучностями 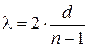 . По определению фазовая скорость связана частотой волны и длиной волны соотношением
. По определению фазовая скорость связана частотой волны и длиной волны соотношением 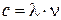 . Окончательно получаем:
. Окончательно получаем:  .
.
Приступая к работе необходимо
Знать определения
волны;
амплитуды, частоты, фазы, начальной фазы, периода волны, длины волны, волнового вектора,
фазовой скорости волны;
стоячей волны.
Знать
вид динамического и кинематического уравнений волны;
выражения для фазовых скоростей упругих волн через параметры среды.
Уметь
пользоваться вольтметром;
оценивать случайные погрешности прямых и косвенных измерений.
Цели работы
Проверка закона дисперсии звуковых волн в воздухе.
Решаемые задачи
ü Знакомство с методом измерения скорости звуковых волн методом стоячей волны;
ü Определение узлов и пучностей стоячих звуковых волн при помощи микрофона;
ü Измерение длин звуковых волн разной частоты в воздухе.
Экспериментальная установка
Приборы и принадлежности:
ü широкополосный динамик (1);
ü генератор звуковых колебаний (2);
ü многофункциональный микрофон (3);
 Рис.1. Схема экспериментальной установки
Рис.1. Схема экспериментальной установки
|
ü вольтметр (4);
ü отражающая поверхность (5).
В эксперименте, динамик, который излучает гармонические звуковые волны (синусоидальные) с регулируемой частотой n, помещается перед отражающей плоскостью на расстоянии, большем, чем длина волны. В результате сложения первичной и отраженной волн образуется стоячая волна. Для обнаружения стоячей волны используется микрофон, выходной сигнал c которого измеряется при помощи вольтметра.
Порядок выполнения работы
Подготовка установки для проведения экспериментов
1. Поместите динамик напротив отражающей пластины на расстоянии примерно 1.5 м;
2. Подсоедините динамик к генератору (тип сигнала: синусоидальный, диапазон частот: кГц).
3. Подсоедините микрофон (режим «=» см рис.1) к вольтметру (предел измерений 3 В);
4. Поместите микрофон на линии между динамиком и отражающей пластиной, разверните микрофон по направлению к пластине.
Проведение измерений
5. Установите генератор на частоту 9 кГц;
6. Включите микрофон и вольтметр, используя микрофон, найдите максимум напряжения;
7. Отрегулируйте громкость путем изменения амплитуды выходного сигнала генератора так, что бы напряжение на микрофоне превышало 3 В;
8. Перемещайте микрофон, что бы определить позиции минимумов и максимумов напряжения, отметьте эти положения;
9. Измерьте расстояния d между первым и последним n наблюдаемым положениями максимумов при помощи рулетки и запишите их;
10. Повторите эксперимент с различными частотами: 7, 5, 3, 2 и 1 кГц.
Обработка и представление результатов
По результатам измерений, и проведя вычисления, заполните таблицу.
| n, кГц | N | d, см | l = 2· d /(n -1), см | с = l·n, м |
| … |
Постройте графики зависимостей λ(n) и c (n).
Сделайте вывод о зависимостях λ(n) и c (n).
Лабораторная работа № 193. Исследование зависимости частоты колебаний струны от ее длины и натяжения
Введение
В натянутой струне, закрепленной с обоих концов, при возбуждении какого-либо произвольного поперечного возмущения возникнет довольно сложное волновое движение. Однако определенных частотах, когда на длине струны L укладывается целое число полуволн: L = n ∙λ/2 (n - целое число), возможно движение в виде стоячей волны. Если длина струны L равна половине длины волны основной моды (n = 1) колебаний, то L = λ/2. Поэтому частота v 1 основного тона (т.е. звука), издаваемой струной равна
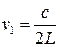 , (1)
, (1)
где c - фазовая скорость волны, распространяющаяся вдоль струны. Эта скорость определяется свойствами струны:
 , (2)
, (2)
где F ‑ сила натяжения струны, S – площадь поперечного сечения, r ‑ плотность струны.
Приступая к работе необходимо
Знать определения
волны;
амплитуды, частоты, фазы, начальной фазы, периода волны, длины волны, волнового вектора,
фазовой скорости волны;
стоячей волны.
Знать
вид динамического и кинематического уравнений волны в струне;
условия появления стоячих волн;
выражения для фазовых скоростей упругих волн в струне.
Уметь
запускать программы в среде Windows и пользоваться стандартными элементами их интерфейса (меню, контекстные меню, окна и т.д.);
оценивать случайные погрешности прямых и косвенных измерений.
Цель работы
Исследование акустических колебаний струны.
Решаемые задачи
ü наблюдение зависимостей частот колебаний струны от силы натяжения струны и её длины;
ü измерение частоты колебаний струны в зависимости от силы натяжения струны;
ü измерение частоты колебания струны в зависимости от её длины;
ü определение плотности струны;
ü определение скорости волны в натянутой струне.
Экспериментальная установка
Приборы и принадлежности:
ü Монохорд (1)
ü 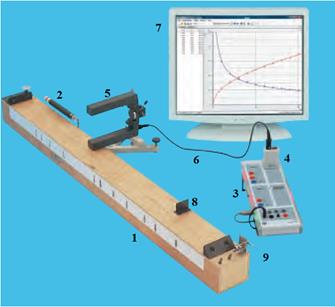 ü Рис.1. Экспериментальная установка для исследования колебаний струны.
ü Рис.1. Экспериментальная установка для исследования колебаний струны.
|
ü Прецизионный динамометр, 20 Н (2)
ü Компьютерный интерфейс сенсор - CASSY 2 (3)
ü Адаптер Timer S (4)
ü П-образный прерыватель света (5)
ü Многожильный кабель, 1,5 м (6)
ü Микрометр и линейка 1,2 м.
ü Компьютер с установленной программой CASSY Lab 2 (7)
В эксперименте частота колебаний n и, соответственно, высота звука струны измеряется как функция длины струны L и силы натяжения F. Для этого компьютерный интерфейс сенсор - CASSY 2 используется как секундомер с высоким разрешением, для измерения периода колебаний T.
Период колебаний T измеряется посредством перекрывания света, используя П-образный прерыватель света (5), который устанавливается между деревянной резонансной коробкой монохорда (1) и струной. Прерыватель света (5) связан с входом A сенсора - CASSY (3) через Timer S (4) с помощью многожильного кабеля (6).
Примечания к эксперименту
Для оптимального измерения периода T колебаний, положение П-образного прерывателя света всегда должно находиться в средне колеблющейся части струны.
Период колебаний T определяется однозначно, если струна в течение периода дважды перекрывает луч света. Для этого случае струна должна быть расположена так, чтобы красный светодиод с внутренней стороны П-образного прерывателя света перекрывался струной, когда струна находится в положении равновесия. Кроме того, при фиксировании показаний периода обращайте внимание на то, что упомянутый красный светодиод оказывается между предельными отклонениями струны. Лучший результат получается, если струна располагается непосредственно над меньшим отверстием. При необходимости поверните П-образный прерыватель света.
При возбуждении струна должна совершать колебания параллельно поверхности резонансной коробки (монохорда).
Сила натяжения струны F измеряется с помощью отградуированного динамометра (2), см. рис.1. Натяжение струны на монохорде может изменяться с помощью поворачивающегося ключа (9).
При проведении эксперимента, наилучшие результаты получаются, если сначала сила натяжения струны устанавливается около 100 Н, а сила натяжения уменьшается.
При проведении измерений в зависимости от длины струны L, её длина изменяется с помощью смещающегося мостика (8). Когда струна возбуждается, не трогайте другой рукой части струны, которые не участвуют в колебании.
Порядок выполнения работы
Упражнение 1. Измерения частоты колебаний струны от её силы натяжения
1. Подключите интерфейс CASSY 2 и компьютер к электрической сети 220 В, войдите в систему Windows;
2. На Рабочем столе Windows нажмите иконку упражнения.
3. На переднем плане возникнет окно с именем “CASSYs”. Щелкните в нем кнопку “Show measuring parameters” - в правой части основного окна программы появится окно “Settings”. Закройте окно “CASSYs”.
4. Установите величину силы F натяжения струны в диапазоне 90÷100 Н, поворачивая ключ натяжения струны.
5. Поместите одну ветвь П-образного прерывателя света под струной, находящейся в покое. Проверьте, находится ли маленькое отверстие инфракрасного луча (отверстие с внутренней стороны прерывателя) под струной. Красный светодиод сбоку ворот при этом должен не гореть.
6. Создайте, некоторым поперечным усилием, колебания струны. Во время колебания струны светодиод должен светиться. Через 2-3 секунды нажмите клавишу F9. При этом отображаемые на дисплее компьютера будут занесены в таблицу.
7. Повторите измерения (7-9 раз) для меньших значений силы F.
8. Измерьте длину и поперечное сечение струны.
9. Сохраните данные под своим именем, например, Lab15упр1Sidorov.
Упражнение 2. Измерения частоты колебаний струны от её длины
10. Подключите интерфейс CASSY Lab 2 и компьютер к электрической сети 220 В, войдите в систему Windows;
11. На Рабочем столе Windows нажмите иконку упражнения.
12. На переднем плане возникнет окно с именем “CASSYs”. Щелкните в нем кнопку “Show measuring parameters” - в правой части основного окна программы появится окно “Settings”. Закройте окно “CASSYs”.
13. Установите необходимую (например, L/2) длину струны, передвигая мост (8), см. рис.1.
14. Измерьте длину струны и запишите её значение в таблицу компьютера.
15. Поместите одну ветвь П-образного прерывателя света под струной, находящейся в покое. Проверьте, находится ли маленькое отверстие инфракрасного луча (отверстие с внутренней стороны прерывателя) под струной. Красный светодиод сбоку ворот при этом должен не гореть.
16. Создайте, некоторым поперечным усилием, колебания струны. Во время колебания струны светодиод должен светиться. Через 2-3 секунды нажмите клавишу F9. При этом отображаемые на дисплее компьютера будут занесены в таблицу.
17. Повторите измерения (7-9 раз) для других значений длины L струны.
18. Запишите в директорию Рабочего стола, файл выполненной работы под своим именем, например, Lab15упр2Sidorov.
Обработка и представление результатов
При изменении силы натяжения струны зависимости T (F) и n(F) сразу появляются во время измерения. В окне программы “Evaluation”, отображается квадрат частоты n как функция силы F натяжения струны. Линейная зависимость между n2 и F устанавливается посредством подгонки первичных измерений (используя правую кнопку мыши). Покажите, что частота колебаний струны не зависит способ удара и воздействия на струну и частота колебаний струны возрастает с увеличением силы натяжения. Из графика зависимости n2(F) по тангенсу угла наклона, используя формулы (1) и (2), определите плотность r струны. Сделайте вывод и сравните значение плотности r данной струны с известными значениями.
При изменении длины струны зависимости T (L) и n(L), аналогично, сразу появляются во время измерения. В окне программы “Evaluation”, отображается зависимость частоты n как функция обратной длины 1/ L. Точная зависимость между n и 1/ L устанавливается посредством подгонки первичных измерений (используя правую кнопку мыши). Покажите, что частота колебаний струны возрастает с уменьшением длины струны. Определите, используя формулы (1) и (2), скорость волны c, распространяющаяся вдоль струны. Сделайте вывод о полученных результатах.
Данные эксперимента представьте в виде таблиц, аналогичных тем, которые представлены в CSSY Lab 2. (Перенести данные в любой документ Office, можно выделив необходимый участок таблицы с помощью клавиш со стрелками при нажатой клавише “Shift”, и используя затем стандартные Ctrl-C и Ctrl-V).
Лабораторная работа № 194. Измерение скорости звуковых импульсов в твёрдых телах
Введение
Скорость импульса с можно измерить, определив время его прохождения t между краями образца известной длины l. c = l /t.
Если затухание мало эта скорость будет близка к фазовой скорости звуковой продольной волны
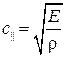 (1)
(1)
где E – модуль Юнга, а r– плотность материала стержня.
Приступая к работе необходимо
Знать определения
волны;
амплитуды, частоты, фазы, начальной фазы, периода волны, длины волны, волнового вектора,
фазовой скорости волны;
продольной и поперечной волны;
скорости звука;
Знать
вид динамического и кинематического уравнений волны;
выражения для фазовых скоростей упругих волн через параметры среды.
Уметь
запускать программы в среде Windows и пользоваться стандартными элементами их интерфейса (меню, контекстные меню, окна и т.д.);
оценивать случайные погрешности прямых и косвенных измерений.
Цель работы
Определение скорости звука в алюминиевом, медном, латунном и стальном стержнях.
Решаемые задачи
ü Знакомство с методом измерения скорости звуковых импульсов в твердых телах;
Экспериментальная установка
Приборы и принадлежности:
ü Набор из четырех металлических стержней;
ü Пьезоэлектрическая опора 1 (см рис.);
ü Струбцина 2, с крепежными винтами 3;
ü Молоточек;
ü Компьютерный интерфейс - Sensor CASSY 2 4;
ü Компьютер.
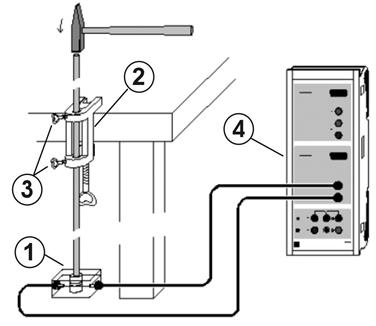 В данном измерении используются множественные отражения коротких звуковых импульсов на концах стрежня. Начальный импульс получается в результате лёгкого удара молоточком по верхнему концу стержня. Импульс последовательно отражается несколько раз от концов стрежня. Достигая нижнего конца стержня, импульс всякий раз оказывает избыточное давление на чувствительную пьезоэлектрическую опору. Время ∆ t между двумя последовательными надавливаниями можно зафиксировать с помощью CASSY. Очевидно, что если длина стержня равна s, то
В данном измерении используются множественные отражения коротких звуковых импульсов на концах стрежня. Начальный импульс получается в результате лёгкого удара молоточком по верхнему концу стержня. Импульс последовательно отражается несколько раз от концов стрежня. Достигая нижнего конца стержня, импульс всякий раз оказывает избыточное давление на чувствительную пьезоэлектрическую опору. Время ∆ t между двумя последовательными надавливаниями можно зафиксировать с помощью CASSY. Очевидно, что если длина стержня равна s, то
с = 2 s /∆ t. (2)
Порядок выполнения работы:
Подготовка установки для проведения экспериментов
1. Включите в сеть Sensor CASSY и компьютер.
2. На Рабочем столе Windows найдите ярлык работы и стартуйте его.
3. Закройте лишние окна. Удалите результаты предыдущих измерений.
Проведение измерений
4. Выберите один из четырёх металлических стержней;
5. Вывиньтите крепежные винты 3 до тех пор, чтобы исследуемый стержень свободно проходил через крепежные отверстия в струбцине. Аккуратно проденьте стержень через крепления на струбцине, и опустите его на пьезоэлектрическую опору. Внимание!!! Не допускайте удара стержня об пьезоэлектрическую опору;
6. Аккуратно зажмите стержень на струбцине при помощи крепёжных винтов 3. Проверьте зажим! Если Вы не сможете вытащить стержень из струбцины – зажим достаточен;
7. Запустите измерение, нажав клавишу F9. (в данной программе измерения давления начнут запоминаться после первого резкого нажатия на пьезоэлектрическую опору);
8. Стукните верхний конец первого металлического стержня молоточком. Внимание!!! Достаточно небольшого по силе удара, с расстояния 5-10 см.
9. Через некоторое время остановите измерения, нажав клавишу F9.
10. Определите времена ∆ t i между двумя последовательными импульсами. Для этого используйте то обстоятельство, что при щёлканьи мышкой по точке на графике, компьютер выделит соответствующее значение в таблице слева. Обратите внимание, что время в данной работе измеряется в миллисекундах.
11. По серии измерений ∆ t i рассчитайте ∆ t пользуясь алгоритмом статистической обработки результатов прямых измерений
12. Вычислите скорость звука с по формуле (2). Оцените погрешность.
13. Сохраните полученные зависимости в папку Документы/Students/папка с номером вашей группы/ Сохраните файл под своей фамилией.
14. Повторите п.п. 4-12 для остальных трех стержней.
Обработка и представление результатов
Данные экспериментов представьте в виде таблицы.
| Металл | Эксперимент, м/с | Скорость звука (литерат. данные), м/с |
| Латунь | ... | |
| Медь | ||
| Алюминий | ||
| Сталь |
Сделайте вывод о скорости звуковых импульсов в различных твердых телах.
Приложение 1. Алгоритмы статистической обработки результатов измерений
Результаты измерений некоторой физической величины f должны быть представлены в виде
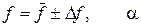 .
.
где 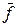 называется средним значением величины f,
называется средним значением величины f, 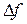 - пределом абсолютнойпогрешности измерения,
- пределом абсолютнойпогрешности измерения, 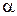 - доверительной вероятностью.
- доверительной вероятностью.
Такая запись означает, что истинное значение величины f с вероятностью a лежит в границах доверительного интервала 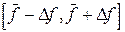 .
.
Обработка результатов прямых измерений
1. Полученные результаты отдельных измерений x iзанесите в таблицу.
2. Вычислите среднее арифметическое
 (1)
(1)
3. Определите среднеквадратичную погрешность среднего значения
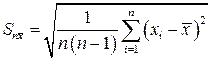 . (2)
. (2)
4. По заданному значению коэффициента надежности a и известному числу измерений по таблице из Приложения 2 определите коэффициент Стьюдента t a, n .
5. Определите инструментальную погрешность измерительного прибора D x и (по паспортным данным, по классу точности, либо как половина цены минимального деления шкалы прибора).
6. Рассчитайте предел абсолютной погрешности измерения
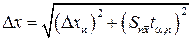 . (3)
. (3)
Для упрощения расчетов можно сначала отдельно рассчитать величины, стоящие в формуле (3) в скобках. Если одна из них в 2 или более раза меньше другой, то ею можно пренебречь и необходимость возведения во вторую степень и извлечения квадратного корня отпадет.
7. Вычислите относительную погрешность
 (4)
(4)
8. Результат измерения представьте в виде:
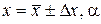 . (5)
. (5)
Обработка результатов косвенных измерений
Если искомая величина F = F (x, y,..., z) является функцией одной или нескольких величин x, y,..., z, получаемых в ходе прямых измерений, алгоритм оценки погрешности таков.
1. По алгоритму описанному выше найдите погрешности прямых измерений D x,D y,...,D z. При этом не обязательно проводить одинаковое число измерений каждой из величин x, y,..., z.
2. Рассчитайте среднее значение величины F
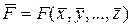 (6)
(6)
3. Найдите выражения для частных производных функции F, по переменным x, y,..., z:
 (7)
(7)
4. Оцените искомую погрешность D F по формуле:
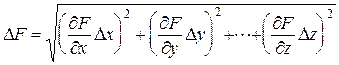 (8)
(8)
Заметим, что для часто встречающихся функций вида
F = Const×xayb×...×zc,
удобно пользоваться формулой, дающей слегка завышенную по сравнению с (7) оценку погрешности:
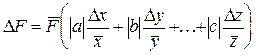 . (9)
. (9)
5. Результат измерения представьте в виде:
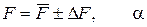 . (10)
. (10)
ПРИЛОЖЕНИЕ 2. ТАБЛИЦА КОЭФФИЦИЕНТОВ СТЬЮДЕНТА.
| n | a | |||||
| 0,70 | 0,80 | 0,90 | 0,95 | 0,98 | 0,99 | |
| 2,0 | 3,1 | 6,3 | 12,7 | 31,8 | 63,7 | |
| 1,3 | 1,9 | 2,9 | 4,3 | 7,0 | 9,9 | |
| 1,3 | 1,6 | 2,4 | 3,2 | 4,5 | 5,8 | |
| 1,2 | 1,5 | 2,1 | 2,8 | 3,7 | 4,6 | |
| 1,2 | 1,5 | 2,0 | 2,6 | 3,4 | 4,0 | |
| 1,1 | 1,4 | 1,9 | 2,4 | 3,1 | 3,7 | |
| 1,1 | 1,4 | 1,9 | 2,4 | 3,0 | 3,5 | |
| 1,1 | 1,4 | 1,9 | 2,3 | 2,9 | 3,4 | |
| 1,1 | 1,4 | 1,8 | 2,3 | 2,8 | 3,3 | |
| 1,1 | 1,4 | 1,8 | 2,2 | 2,8 | 3,2 | |
| 1,1 | 1,4 | 1,8 | 2,2 | 2,7 | 3,1 | |
| 1,1 | 1,4 | 1,8 | 2,2 | 2,7 | 3,1 | |
| 1,1 | 1,4 | 1,8 | 2,2 | 2,7 | 3,0 | |
| 1,1 | 1,3 | 1,8 | 2,1 | 2,6 | 3,0 | |
| 1,1 | 1,3 | 1,8 | 2,1 | 2,6 | 2,9 | |
| 1,1 | 1,3 | 1,7 | 2,1 | 2,6 | 2,9 | |
| 1,1 | 1,3 | 1,7 | 2,1 | 2,6 | 2,9 | |
| 1,1 | 1,3 | 1,7 | 2,1 | 2,6 | 2,9 | |
| 1,1 | 1,3 | 1,7 | 2,1 | 2,5 | 2,9 | |
| ... | ... | ... | ... | ... | ... | ... |
| ¥ | 1,0 | 1,3 | 1,6 | 2,0 | 2,3 | 2,6 |
Пприложение 3. Таблица производных некоторых функций.
| функция f (x) | производная f '(x) |
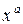
| axa –1 |
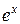
| 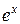
|
| ax | ax ln(a) |
| ln(x) | 1/ x |
| log ax | 1/ x ln(a) |
| sin(x) | cos(x) |
| cos(x) | –sin(x) |
| tg(x) | 1/cos2 (x) |
| arcsin(x) | 1/(1– x 2)1/2 |
| arccos(x) | –1/(1– x 2)1/2 |
| arctg(x) | 1/(1+ x 2) |
| arcctg(x) | –1/(1+ x 2) |
Приложение 4. Краткое описание простейших измерительных приборов
Нониус
Нониусом называют вспомогательную шкалу измерительных приборов, которая служит для отсчета дробных долей делений основной шкалы. Нониус позволяет повысить точность измерений в 10-20 раз.
В большинстве приборов используются линейные или угловые (круговые) шкалы. Отсчет по прибору представляет собой измерение длин отрезков прямой или дуги. В том случае, когда относительная точность измерения длины такова, что можно удовлетвориться абсолютной точностью в сотые или даже десятые доли миллиметра, а для углов - минутами или долями минут, для увеличения точности измерения можно пользоваться обычными масштабными линейками и угломерами, снабженными нониусами.
 Рис. 1.
Рис. 1.
|
Самым простым является десятичный нониус, который дает возможность измерять длину с точностью до 0,1 деления основной шкалы (масштаба). Этот нониус представляет собой дополнительную линейку, разбитую на 10 равных делений. Длина всего нониуса равна девяти целым делениям масштаба. Таким образом, если длина одного деления нониуса Х, а длина одного деления масштаба Y = 1 мм, то 10× Х = 9 мм. Следовательно, длина каждого деления нониуса будет равна 0,9 мм. Если нулевой штрих нониуса, а, следовательно, и десятый, точно совпадает с каким-либо штрихом масштаба, то все остальные штрихи нониуса не совпадают со штрихами масштаба (рис. 1а). Если же нулевой штрих нониуса не совпадает с масштабным, то найдется такой штрих, который совпадает с каким-либо штрихом масштаба гораздо лучше (рис. 1б).
Наименьшая величина, которая может быть измерена при помощи нониуса, определяется разностью D Х = Y - X между длиной масштаба и длиной деления нониуса. Эта разность и будет в нашем случае ценой деления или же точностью нониуса: при Х = 0,9 мм, Y = 1 мм, D Х = 0,1 мм.
Как пользоваться нониусом
При снятии отсчета требуется определять расстояние L между нулями нониуса и основной шкалы.
В изображенной на рис. 1б ситуации это расстояние складывается из 10 делений масштаба, «пройденных» нулем нониуса, то есть из 10 мм и отрезка D L, длина которого равна расстоянию от десятого штриха масштаба до нуля нониуса с точностью до 0,1 мм.
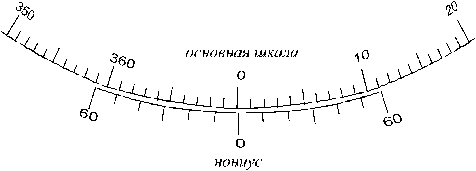 Рис. 2.
Рис. 2.
|
Как видно из рисунка 1б, восьмой штрих нониуса, отмеченный стрелкой, точно совпадает с масштабным штрихом. Седьмой штрих не совпадает с масштабным штрихом настолько, насколько длина деления нониуса короче длины деления масштаба, то есть на 0,1 мм. Шестой штрих нониуса не совпадает с масштабным штрихом уже на 0,2 мм, так как длина двух делений нониуса на 0,2 мм короче длины двух делений масштаба. Нулевой штрих нониуса не совпадает с масштабным штрихом уже на 0,8 мм, так как восемь делений нониуса короче восьми делений масштаба на 0,8 мм. Расстояние между нулевым штрихом нониуса и десятым штрихом масштаба как раз равно отрезку D L. Таким образом, отрезок D L равен 0,8 мм. Другими словами, для нахождения десятых долей деления шкалы при помощи десятичного нониуса надо номер «совпадающего» деления нониуса умножить на 0,1, то есть на цену деления нониуса.
Круговой нониус, в принципе, не отличается от линейного, кроме того, что здесь вместо линейных величин следует пользоваться угловыми. Он представляет собой небольшую дуговую линейку, скользящую вдоль круга (лимба) (см. рис. 2).
Штнгенциркуль
Штангенциркулем (рис. 3) называется прибор, применяющийся для измерения линейных размеров с точностью от 0,1 до 0,02 мм.
Штангенциркуль состоит из линейки (штанги) 1 с миллиметровыми делениями и подвижной рамки 2 с нониусом 3 и фиксирующим винтом 4. На штанге и рамке имеются ножки (губки) 5 и 6. Ножки с внутренней стороны имеют плоские поверхности. При сомкнутых ножках отсчет по нониусу равен нулю. Для измерения штангенциркуль берут в правую руку, а измеряемый предмет помещают между ножками, плотно зажимают и закрепляют винт. После этого производят отсчет. Многие штангенциркули снабжены еще одной рамкой 7 с закрепляющим 8 и микрометрическим 9 винтами. Для более точного отсчета измерения можно поступать следующим способом. Измеряемый предмет слегка зажимают между ножками. Закрепляют винт 8, и при помощи винта 9 рамка 2 более плотно (но без сильного нажима) прижимается к предмету. Затем закрепляют винт 4 и производят отсчет.
 Рис.3.
Рис.3.
|
Для измерения внутренних размеров пользуются специально отшлифованными внешними сторонами ножек со стороны тупых концов, суммарная толщина которых известна и нанесена на них в миллиметрах. Ножки вставляют внутрь отверстия, а затем раздвигают. К отсчету по нониусу следует прибавить толщину ножек.
Микрометр
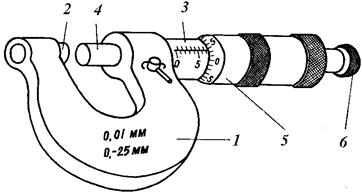 Рис. 4.
Рис. 4.
|
Микрометр (рис.4) представляет собой прибор, предназначенный для измерения линейных размеров с точностью до 0,01 мм. Микрометр для измерения наружных размеров в пределах от 0 до 25 мм состоит из скобы 1 с пяткой 2 и трубкой (стеблем) 3. В трубке имеется внутренняя резьба, в которую ввинчен микрометрический винт 4 с закрепленным на нем барабаном 5. На конце барабана имеется фрикционная головка (трещотка) 6.
Действие микрометра основано на свойстве винта совершать при его повороте поступательное перемещение, пропорциональное углу поворота. При измерении предмет зажимается между пяткой и микрометрическим винтом. Для вращения барабана при этом пользуются только фрикционной головкой. После того, как достигнута предельная степень нажатия на предмет (500-600 г), фрикционная головка начинает проскальзывать, издавая характерный треск. Благодаря этому, зажатый предмет деформируется сравнительно мало (его размеры не искажаются).
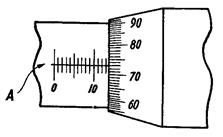 Рис.5.
Рис.5.
|
На трубке 3 нанесены деления основной шкалы. Барабан 5 при вращении винта перемещается вдоль трубки. Шаг винта подбирается таким, что один полный оборот барабана соответствует его смещению вдоль основной шкалы на одно деление. На барабане нанесена добавочная шкала.
Основная шкала микрометра разбита на миллиметры. Шаг микрометрического винта также равен 1 мм. На шкале барабана нанесено 100 равных делений. Ясно, что каждое из этих ста делений имеет достоинство 0,01 мм, так как при повороте барабана на одно деление происходит поступательное перемещение микрометрического винта на 0,01 мм. Если нулевое деление барабана совпадает с прямой линией А на трубке (рис.5), то микрометр показывает целое число миллиметров, которое определяется делением основной шкалы, показавшимся из-под барабана. Если же нуль шкалы барабана не совпадает с линией на трубе, то отсчет не равен целому числу миллиметров. В этом случае число целых миллиметров определяется последним видимым делением основной шкалы, а число сотых долей миллиметра - делением барабана, стоящим против линии на трубки. На рис. 5 измеряемая длина равна 13,73 мм.
Перед началом работы с микрометром следует убедиться в его исправности. Для этого вращением фрикционной головки приводят в соприкосновение микрометрический винт с пяткой. Момент соприкосновения определяется по сигналу трещотки. При этом край барабана должен располагаться над нулевым делением основной шкалы, а нуль барабана - против линии на трубке. Если эти условия не соблюдены, то во всех дальнейших измерениях следует учитывать систематическую ошибку микрометра, равную тому числу делений барабана, которое соответствует сомкнутым микрометрическому винту и пятке. Если это отклонение велико, то микрометр нуждается в регулировке. Вращать винт с усилием (за барабан) после того, как заработала трещотка, запрещается, так как это ведет к порче прибора.
Особенности отсчета
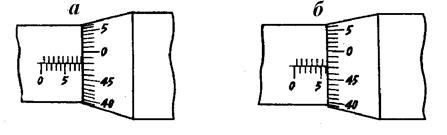 Рис. 6.
Рис. 6.
|
Когда отсчеты по шкале барабана немного меньше 50 (или 100), следующее деление шкалы барабана обычно показывается из-под края барабана. Это особенно актуально при измерениях микрометрами, имеющими шкалы с половинными делениями. Такая шкала изображена на рис. 6. Верхний ряд делений на основной шкале отмечает половинные доли основной шкалы. Естественно в этом случае шкала барабана имеет в два раза меньше делений, чем изображенная на рис. 5.
Последнее видимое нижнее деление на рис. 6а соответствует 8 мм и, кроме того, показалось еще верхнее деление. Возникает вопрос, как правильно отсчитывать число целых и половинных делений: 8,0 мм или 8,5 мм? В этом случае появившееся верхнее деление не должно приниматься в расчет, так как показания шкалы барабана, равные 48 делениям, говорят о том, что край барабана отошел от последнего нижнего видимого восьмого деления на 0,48 мм; следовательно, в данном случае отсчет будет 8,0 + 0,48 = 8,48 мм. Если бы край барабана отошел на 0,48 мм от верхнего деления, то между этим делением и барабаном был бы заметный просвет почти полмиллиметра. На рис. 6б показано положение барабана, при котором из-под его края уже видно шестое деление основной шкалы. Однако, отсчет по барабану 0,47 мм. Это означает, что до шестого целого миллиметра нужно повернуть барабан на три деления его шкалы (переместить край барабана на 0,03 мм). Таким образом, в этом случае шестое деление основной шкалы не следует принимать во внимание и, следовательно, отсчет будет равен 5,0 + 0,5 + 0,47 = 5,97 мм.
Ручной механический секундомер 1
Секундомер предназначен для измерения малых промежутков времени (до 30 мин.). У секундомера имеются две стрелки: большая - секундная и малая - минутная. Цена деления самого мелкого деления секундной шкалы 0,2 сек. Секундная стрелка движется скачками также через 0,2 сек. Поэтому наибольшая абсолютная точность, которую можно достичь секундомером, составляет 0,2 сек. За один оборот секундной стрелки минутная стрелка проходит одно деление. Полный оборот малая стрелка совершает за 30 минут.
Правила пользования секундомером.
Секундомер запускают, нажимая на головку до упора. При вторичном нажатии обе стрелки останавливаются. При третьем нажатии остановленные стрелки возвращаются к нулевым делениям своих шкал. Нажимать нужно резко, после каждого нажатия нужно дать головке подняться вверх. Заводят секундомер, вращая заводную головку до отказа. Последние два-три оборота заводной головки следует делать осторожно во избежании обрыва пружины. В конце работы секундомер не следует останавливать до полного спуска пружины. Секундомер следует охранять от ударов, сильных сотрясений, попадания в него воды, а также от магнитных полей.
О точности измерений
Точность измерения времени секундомером зависит не только от точности самого секундомера, но и от навыков наблюдателя, в частности, от того, одинакова ли быстрота его реакции при пуске секундомера. При известных навыках точность измерений секундомером может быть доведена до его технической точности, то есть до 0,2 сек. Это абсолютная точность. Относительная же точность зависит еще и от того, какой промежуток времени измеряют. Если этот промежуток - одна секунда, то относительная точность составляет  . Если же измеряется промежуток времени 100 секунд, то относительная точность будет уже
. Если же измеряется промежуток времени 100 секунд, то относительная точность будет уже 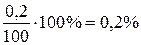 . Поэтому, при измерении времени секундомером стремятся добиться таких условий опыта, при которых измеряемый промежуток времени будет достаточно велик. В частности, если измеряется период колебаний, и есть уверенность, что он не меняется в процессе колебаний, то измеряют время десятков или даже сотен колебаний подряд. Чтобы найти период колебаний, делят найденное время на число колебаний. Следует заметить, что увеличение измеряемого промежутка времени приводит к увеличению точности только до определенных пределов. Для больших промежутков времени относительная точность ограничивается правильностью хода секундомера. В частности, секундомеры СМ-60 регулируют обычно так, что ошибка за 30 минут составляет до 1,6 секунд, что составляет ошибку 0,1%. Таким образом, увеличивать промежуток времени для получения большой точности целесообразно лишь до 200-300 секунд (3-5 минут), если не выверять специально секундомер и не вносить затем поправки на его неправильный ход.
. Поэтому, при измерении времени секундомером стремятся добиться таких условий опыта, при которых измеряемый промежуток времени будет достаточно велик. В частности, если измеряется период колебаний, и есть уверенность, что он не меняется в процессе колебаний, то измеряют время десятков или даже сотен колебаний подряд. Чтобы найти период колебаний, делят найденное время на число колебаний. Следует заметить, что увеличение измеряемого промежутка времени приводит к увеличению точности только до определенных пределов. Для больших промежутков времени относительная точность ограничивается правильностью хода секундомера. В частности, секундомеры СМ-60 регулируют обычно так, что ошибка за 30 минут составляет до 1,6 секунд, что составляет ошибку 0,1%. Таким образом, увеличивать промежуток времени для получения большой точности целесообразно лишь до 200-300 секунд (3-5 минут), если не выверять специально секундомер и не вносить затем поправки на его неправильный ход.
Лабораторные весы
 Рис.7.
Рис.7.
|
Используемые в практикуме лабораторные весы (рис. 7) представляют собой рычажные весы. Момент веса чаши с исследуемым предметом уравновешивается моментом веса гирь. Последний меняется за счет перемещения гирь по нескольким рельсам. Напротив фиксированных положений гирь выгравированы значения уравновешиваемой массы.
Точность весов составляет 0,01 г, предел измерения 311г.
Весы снабжены арретиром - приспособлением, закрепляющим коромысло весов в нерабочем состоянии и предохраняющим ребро призмы от изнашивания. Обычно, весы должны быть арретированы (коромысло закреплено). При взвешивании коромысло освобождается поворотом лапки вблизи снования весов.
Перед взвешиванием следует убедиться, правильно ли установлены весы по отвесу и находятся ли они в равновесии без нагрузки при освобождении арретира. В случае необходимости при крайних левых положениях грузов необходимо добиться равновесия, перемещая по винту груз вблизи точки крепления чаши к коромыслу.
Чтобы определить, находятся ли весы в равновесии, нет необходимости ждать, пока они остановятся. Весы уравновешены, если стрелка при их качании отклоняется на одинаковое число делений относительно положения равновесия.
Правила взвешивания
Ставить на чашу весов, а также снимать с неё грузы можно только при арретированных весах.
При взвешивании следует придерживаться определенного порядка.
Первым перемещают гирьку, которая, по мнению взвешивающего, наверняка перетянет тело. Если перетягивает разновес, то гирьку смещают влево на одно деление до того момента, когда тело начнет перетягивать грузики. Если же перетягивает тело, то гирьку перемещают вправо до тех пор пока разновес не перетянет тело, а затем смещают на одно деление влево.
Затем повторяют действия для меньшей гирьки.
Процесс продолжается до уравновешивания весов.
Весы считаются уравновешенными, если стрелка при освобождении от арретира отклоняется по обе стороны от нуля примерно на одинаковое число делений.
Масса чаши с исследуемым телом вычисляется как сумма выгравированных чисел напротив гирь.
1 В этой работе нумерация формул дана по Приложению 1.
[1] После консультации с преподавателем
[2] После консультации с преподавателем
1 Здесь и далее для простоты полагается, что мы имеем дело только с изотропными материалами.
1 Хорошие результаты получаются и в случае, если вместо описанного здесь механического секундомера использовать наручные электронные часы в режиме секундомера.






