Лабораторная работа № 151. Измерение моментов инерции тел правильной формы.
Введение
Основное уравнение динамики вращательного движения в случае неподвижной оси вращения z удобно спроектировать на эту ось:
 . (1)
. (1)
Здесь Lz - проекция момента импульса, Mz - момент внешних сил относительно оси.
Проекция момента импульса Lz связана с угловой скоростью w и моментом инерции I относительно этой оси:
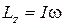 . (2)
. (2)
Момент инерции тела определяется формулой:
 , (3)
, (3)
где суммирование проводится по всем материальным точкам тела с массами m i, r i - расстояния от материальных точек до оси вращения. В случае непрерывного распределения масс эту формулу можно записать в интегральном виде:
 (4)
(4)
Момент инерции величина аддитивная I =S I i.
При вращении тела под действием момента упругой силы пружины уравнение (1) приводит к следующему соотношению:
I = T 2· D /(4·p2) (5)
где I – момент инерции колеблющегося тела, T – период колебаний, D – модуль кручения пружины. Последние две величины измеряются в данной работе экспериментально.
Приступая к работе необходимо
Знать определения
вектора и составляющей вектора;
координат вектора;
проекции вектора на направление;
вектора угла бесконечно малого поворота, угловой скорости, углового ускорения;
системы координат и системы отсчета;
инерциальной и неинерциальной систем отсчёта;
массы тела, момента инерции тела;
силы, момента силы;
центра масс;
кинетической энергии;
момента импульса.
Знать
формулировку и границы применения уравнения динамики вращательного движения.
Уметь
рассчитывать моменты инерции однородных тел правильной геометрической формы;
измерять расстояния с помощью линейки;
измерять время ручным секундомером;
определять массу взвешиванием;
оценивать случайные погрешности прямых и косвенных измерений.
Цель работы:
Сравнение измеренных и теоретически вычисленных значения моментов инерции тел правильной формы.
Решаемые задачи
ü измерение модуля кручения пружины методом крутильных колебаний;
ü измерение моментов инерции изучаемых тел методом крутильных колебаний.
 Рис.1 Вид экспериментальной установки
Рис.1 Вид экспериментальной установки
|
Экспериментальная установка
Приборы и принадлежности:
ü Торсионная пружина на штативе;
ü Секундомер;
ü Штанга с перемещаемыми грузами;
ü Деревянный шар;
ü Деревянный диск;
ü Держатель для тел цилиндрической формы;
ü Деревянный цилиндр;
ü Полый металлический цилиндр;
ü Весы.
Порядок выполнения работы:
1. Снимите со штанги грузы, установите штангу на пружину и измерьте период колебаний T 0;
2. Определите взвешиванием массы m грузов, закрепляемых на штанге;
3. Установите грузы на штангу, для каждого из шести положений грузов измерьте период T i и вычислите D i = 4·p2· (2· m·R i2)/(T i2 – T 02); Начальная амплитуда колебаний не более 180°!!!
4. Найдите D как среднее измеренных D i;
5. Взвесьте шар, диск, держатель цилиндрических тел, деревянный цилиндр, полый цилиндр.
6. Измерьте диаметры шара, диска, цилиндра и полого цилиндра;
7. Установите на пружину шар, измерьте период колебаний и найдите момент инерции по формуле (5);
8. Установите на пружину диск, измерьте период колебаний и найдите момент инерции по формуле (5);
9. Установите на пружину держатель цилиндрических тел, измерьте период колебаний и найдите момент инерции по формуле (5);
10. Установите на держатель деревянный цилиндр, измерьте период колебаний и найдите суммарный момент держателя и цилиндра. Найдите момент инерции цилиндра как разность суммарного момента инерции и момента инерции держателя;
11. Установите на держатель полый цилиндр, измерьте период колебаний и найти суммарный момент держателя и цилиндра. Найдите момент инерции цилиндра как разность суммарного момента инерции и момента инерции держателя;
Обработка и представление результатов
Вычислите по формулам моменты инерции шара, диска, цилиндра и полого цилиндра и сравните с измеренными.
Моменты инерции однородных тел правильной геометрической формы относительно осей, проходящих через центры масс, приведены в таблице:
| Тело | Ось | Момент инерции |
| Полый однородный тонкостенный цилиндр или кольцо радиуса r и массы m | Ось цилиндра | mr 2 |
| Однородный шар радиуса r | любая ось | 
|
| Однородный диск радиуса r | ось перпендикулярная плоскости диска | 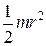
|
| Однородный цилиндр радиуса r и высотой l | ось перпендикулярная оси симметрии | 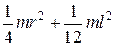
|
| Однородный цилиндр радиуса r и высотой l | ось симметрии | 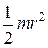
|
| Тонкий однородный стержень длиной l | ось перпендикулярная стержню | 
|
| Однородный куб с длиной ребра l | любая ось | 
|
Данные измерений представьте в виде таблиц:
Таблица I: Таблица II:
| № | R, см | T, с | D |
| - | - | ||
| 5.0 | |||
| 10.0 | |||
| … | … | ||
| 30.0 |
| Тело | m | I эксп | I теор |
| Шар | |||
| Диск | |||
| Цилиндр | |||
| Полый цилиндр |
Сделайте вывод о возможности вычисления моментов инерции однородных тел правильной геометрической формы.
Лабораторная работа № 152. Проверка теоремы Штайнера
Введение
Основное уравнение динамики вращательного движения в случае неподвижной оси вращения z удобно спроектировать на эту ось:
 . (1)
. (1)
Здесь Lz - проекция момента импульса, Mz - момент внешних сил относительно оси.
Проекция момента импульса Lz связана с угловой скоростью w и моментом инерции I относительно этой оси:
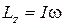 . (2)
. (2)
Момент инерции тела определяется формулой:
 , (3)
, (3)
где суммирование проводится по всем материальным точкам тела с массами m i, r i - расстояния от материальных точек до оси вращения. В случае непрерывного распределения масс эту формулу можно записать в интегральном виде:
 (4)
(4)
Момент инерции величина аддитивная I =S I i.
Момент инерции I тела относительно любой оси АА’ можно найти, зная момент инерции I 0 относительно оси ВВ’, проходящей через центр масс тела параллельно оси АА’ при помощи теоремы Гюйгенса-Штейнера:
I = I 0+ md 2, (5)
где m - масса тела, d - расстояние между осями.
При вращении тела под действием момента упругой силы пружины уравнение (1) приводит к следующему соотношению:
I = T 2· D /(4·p2) (6)
где I – момент инерции колеблющегося тела, T – период колебаний, D – модуль кручения пружины.
Приступая к работе необходимо
Знать определения
вектора и составляющей вектора;
координат вектора;
проекции вектора на направление;
вектора угла бесконечно малого поворота, угловой скорости, углового ускорения;
системы координат и системы отсчета;
инерциальной и неинерциальной систем отсчёта;
массы тела, момента инерции тела;
силы, момента силы;
центра масс;
кинетической энергии;
момента импульса.
Знать
формулировку и границы применения уравнения динамики вращательного движения;
формулировку и границы применения теоремы Гюйгенса-Штайнера.
Уметь
рассчитывать моменты инерции однородных тел правильной геометрической формы;
измерять расстояния с помощью линейки;
измерять время ручным секундомером;
оценивать случайные погрешности прямых и косвенных измерений.
Цель работы:
Сравнение экспериментально определенной и теоретически предсказанной зависимости момента инерции диска от расстояния между осью симметрии диска и осью его вращения.
Решаемые задачи:
ü измерение моментов инерции диска для различных его положений методом крутильных колебаний.
 Рис.1 Вид экспериментальной установки
Рис.1 Вид экспериментальной установки
|
Экспериментальная установка
Приборы и принадлежности:
ü Торсионная пружина на штативе;
ü Секундомер;
ü Исследуемый диск.
Порядок выполнения работы:
1. Установите диск на торсионную пружину так, чтобы ось колебаний проходила через отверстие «0». Измерьте период колебаний T 0. Внимание! Необходимо провести не менее пяти измерений, не менее десяти колебаний в каждом! Начальная амплитуда колебаний не более 180°!
2. Последовательно устанавливая диск так, чтобы ось колебаний проходила через отверстия «2», «4», «6», «8», «10», «12», «14», «16», измерьте периоды колебаний T 1, T 2, …, T 8. Внимание! Так как период колебаний диска может зависеть от положения диска на оси, диск следует ориентировать длинной стороной диска против П-образного кронштейна крутильной пружины!
3. Измерьте радиус диска R.
Обработка и представление результатов
Вычислите относительные теоретические моменты инерции диска по формуле
I т отн = (M·R 2/2+ M·d i2)/(M·R 2/2) = 1 + 2· d i2/ R 2
для всех осей и сравните с экспериментальными результатами, вычисленными с использованием данных измерения по формуле:
I э отн = T 2/ T 02
Данные измерений представьте в виде таблицы:
| № | R, см | T i(1) | T i (2) | T i (3) | T i (4) | T i (5) | 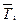
| I т отн |
| 1.00 | ||||||||
| … | … | |||||||
Постройте график зависимости T i2 от I т отн. Сделайте вывод о соответствии теоретических предположений и экспериментального результата.
Лабораторная работа № 153.Изучение прецессии гироскопа
Введение
Гироскопом называется симметричный волчок (т.е. твердое тело, у которого совпадают, по крайней мере, два главных значения тензора инерции I 1 и I 2), совершающий быстрое вращение вокруг оси симметрии (ось 3 на рис.1).
Так как ось вращения совпадает с осью симметрии гироскопа, то его момент импульса равен:
L =I 3 w, (1)
 Рис. 1.
Рис. 1.
|
где I 3 - момент инерции гироскопа относительно оси 3, w - угловая скорость вращения. Из выражения (1) видно, что ось вращения совпадает с направлением вектора момента импульса гироскопа L. Приближенная теория движения гироскопа полагает, что малые по величине моменты внешних сил не могут изменить величину момента импульса L, а меняют только его направление.
Момент импульса гироскопа подчиняется основному закону вращательного движения:
 , (2)
, (2)
где M - суммарный момент внешних сил. Рассмотрим это уравнение применительно к гироскопу, закрепленному в одной точке. Допустим, что точка приложения силы лежит на оси симметрии (см. рис. 1), а сила направлена перпендикулярно оси симметрии 3. Тогда момент этой силы направлен перпендикулярно к оси вращения и L. Под действием момента постоянной силы, вектор L, а следовательно и ось гироскопа, должны совершать равномерное вращение вокруг оси 1. Это вращение называется вынужденной прецессией. Угловая скорость прецессии W может быть найдена из следующих соображений. Поскольку вектор L не меняет своей длины, то изменение этого вектора d L за время dt обусловлено исключительно его вращением со скоростью W и определяется выражением:
 , (3)
, (3)
Из сравнения уравнений (2) и (3) имеем:
 ,
,
или в скалярном виде для данного случая:
 ;
;
откуда
 . (4)
. (4)
Следовательно, при закреплении только одной точки ось гироскопа может совершать движение в пространстве в любом направлении в зависимости от направления момента внешней силы. Такой гироскоп называется свободным. Угловая частота прецессии свободного гироскопа прямо пропорциональна моменту внешней силы и обратно пропорциональна частоте вращения гироскопа вокруг оси симметрии.
Приступая к работе необходимо
Знать определения
вектора и составляющей вектора;
координат вектора;
проекции вектора на направление;
вектора угла бесконечно малого поворота, угловой скорости, углового ускорения;
системы координат и системы отсчета;
инерциальной и неинерциальной систем отсчёта;
массы тела, момента инерции тела;
силы, момента силы;
центра масс;
момента импульса;
углов Эйлера.
Знать
формулировку и границы применения уравнения динамики вращательного движения;
определение гироскопа и уравнение его движения.
Уметь
запускать программы в среде Windows и пользоваться стандартными элементами их интерфейса (меню, контекстные меню, окна и т.д.);
оценивать случайные погрешности прямых и косвенных измерений.
Цель работы
Изучение явления прецессии гироскопа.
Решаемые задачи
ü определение зависимости угловой скорости прецессии от угловой скорости вращения гироскопа;
ü определение зависимости угловой скорости прецессии гироскопа от приложенного момента сил;
ü экспериментальное измерение момента инерции гироскопа;
ü теоретический расчет момента инерции гироскопа.
Экспериментальная установка
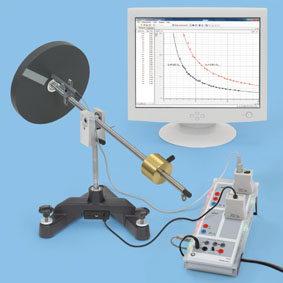
|
Приборы и принадлежности:
ü Гироскоп (масса диска = 1500 г, диаметр = 230 мм);
ü Набор грузов;
ü Шнур для раскрутки гироскопа;
ü Компьютерный интерфейс-сенсор CASSY Lab 2;
ü Компьютер.
Порядок выполнения работы:
Подготовка установки для проведения экспериментов
1. Включите в сеть CASSY Lab и компьютер.
2. На Рабочем столе Windows найдите ярлык работы и стартуйте его.
3. Закройте лишние окна. Удалите результаты предыдущих измерений.
Проведение измерений
4. Возьмите один груз с крючком.
5. Взвесьте груз вместе с крючком и запишите его массу m;
6. Тщательно отгоризонтируйте гироскоп!
7. Измерьте r – расстояние от точки подвеса груза до центра тяжести гироскопа (догадайтесь – где он?);
8. Проверьте, не мешает ли прецессии гироскопа шнур датчика регистрации оборотов гироскопа!
9. Раскрутите гироскоп до угловой скорости вращения примерно w = 15 рад/с. Если после этого ось гироскопа колеблется в вертикальной плоскости, следует сдемпфировать колебания собственной рукой, взявшись за длинный конец оси гироскопа;
10. Подвесьте к длинному концу оси груз;
11. Пронаблюдайте прецессию гироскопа на угол не менее 180 градусов! Прецессия не должна сопровождаться колебаниями оси гироскопа в вертикальной плоскости!
12. Нажмите F9, зафиксировав таким образом измерения угловой скорости собственного вращения гироскопа w и угловой скорости прецессии W;
13. Снимите груз и аккуратно поверните в исходное положение;
14. Занесите измерения в таблицу;
15. Снова подвесьте груз и проведите измерения. Если гироскоп в процессе прецессии заметно (более 10 градусов) отклонился от горизонтали, затормозите его, осторожно прикасаясь (лучше – чистым платком) одновременно к нижней и верхней точкам диска гироскопа и раскрутите его вновь;
16. Выполните описанным выше образом (п.п. 7-14) десять измерений;
17. Заполните таблицу:
| i | wi | Wi | f = w·W |
| … | |||
18. По этим десяти измерениям найдите значение f = w·W для доверительной величины для вероятности 0.95 по алгоритму оценки статистических погрешностей прямых измерений.
19. Проведите измерения f = w·W (п.п. 5-18) еще не менее чем для шести грузов разных масс.
20. Вычислите момент инерции гироскопа I 3теор по его массе и диаметру.
Обработка и представление результатов
По двум-трем сериям для грузов разных масс постройте графики зависимости W(w). Сделайте вывод об этой зависимости.
Постройте график зависимости f(m). Убедитесь в его линейности.
По тангенсу угла наклона этого графика, с учетом формулы (4) найдите момент инерции гироскопа I 3эксп.
Сравните I 3теор и I 3эксп.
.
Лабораторная работа № 154. Проверка уравнения динамики вращательного движения
Введение
Уравнение динамики вращательного движения твердого тела вокруг неподвижной оси z имеет вид:
I zbz= M z, (1)
где I z - момент инерции тела относительно оси z, bz - проекция углового ускорения на ось z, M z - момент силы относительно оси z. Таким образом, устанавливается прямая пропорциональность углового ускорения и момента инерции, что может быть проверено на эксперименте.
Приступая к работе необходимо
Знать определения
вектора и составляющей вектора;
координат вектора;
проекции вектора на направление;
вектора угла бесконечно малого поворота, угловой скорости, углового ускорения;
системы координат и системы отсчета;
инерциальной и неинерциальной систем отсчёта;
массы тела, момента инерции тела;
силы, момента силы;
центра масс;
момента импульса;
углов Эйлера.
Знать
формулировку и границы применения уравнения динамики вращательного движения в векторном виде.
Уметь
запускать программы в среде Windows и пользоваться стандартными элементами их интерфейса (меню, контекстные меню, окна и т.д.);
оценивать случайные погрешности прямых и косвенных измерений.
Цель работы
Проверка линейной зависимости углового ускорения b от момента силы M.
Решаемые задачи
ü измерение углового ускорения;
ü измерение момента сил;
ü экспериментальное определение зависимости углового ускорения от момента сил.
Экспериментальная установка
 Приборы и принадлежности:
Приборы и принадлежности:
ü Диск с тремя разными шкивами, (1)
ü световые ворота со спицевым колесом (2);
ü набор металлических дисков;
ü Компьютерный интерфейс сенсор - CASSY 2 (3);
ü Таймер S (4);
ü Лабораторный столик II, 16 x 13 см (5);
ü Соединительные кабели;
ü Компьютер с установленной программой CASSY Lab.
Диск со шкивами (см. рис.) радиусами r i, (0,012м; 0,024м; 0,048м), может с малым трением вращаться насажены вокруг вертикальной оси. Можно менять момент инерции системы добавляя дополнительные диски. На шкив наматывается нить, к концу которой привязана гирька массы m. Перемещение нити можно зафиксировать с помощью спицевого колеса, которое она вращает.
При падении гири сила натяжения нити T создает момент относительно вертикальной оси z
M z = T r i, (2)
который приводит к вращению системы.
Силу Т можно найти из уравнения поступательного движения гири:
ma = mg - T, (3)
где m - масса гири, а - его ускорение. Из этих уравнений получаем, что момент силы натяжения нити
M z = m (g - a) r. (4)
Варьируя массу гири и радиус шкива, можно менять момент этой силы. В случае плотной намотки нерастяжимой нити ускорение а связано с угловым ускорением b z соотношением b z = a / r. (5)
Ускорение a можно определить дважды численно продифференцировав путь пройденный грузом.
Порядок выполнения работы:
Упражнение 1. Исследование характера движения.
1. Стартуйте с рабочего стола ярлык с названием работы.
2. В появившемся окне настройки подключений нажмите клавишу «Show measuring parameters».
3. Выберите в появившемся списке “Sensor CSSSY2”,“Input A1(Timer)”, “Path βA1”
4. Намотайте нить на один из шкивов и установите 2 гири в верхнем положении, так чтобы крепление колеса не мешало движению груза. Проследите, чтобы нить была натянута горизонтально и ровно вдоль колеса.
5. Введите значение радиуса шкива (0,012м; 0,024м; 0,048м).
6. Обнулите показания угла, нажав клавишу “→0←”.
7. Отпустите гирю и включите измерение, нажав кнопку F9.
8. Повторите опыт для разных шкивов.
9. Рассчитайте соответствующее каждому шкиву ускорение b по формуле (5) и момент силы M по формуле (4).
10. Постройте график зависимости углового ускорения b колеса от момента приложенной силы M. Сделайте вывод о выполнении (невыполнении) уравнения (1).
11. По тангенсу угла наклона графика найдите момент инерции I вращающейся части прибора относительно оси вращения.
Упражнение 2. Исследование зависимости b колеса от его момента инерции I
12. Повторите задание 1выбрав только один радиус шкива, поместив на прибор один, два и три дополнительных диска и подобрав необходимое количество грузов.
13. Проверьте, что момент инерции увеличивается на одинаковую величину.
КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ К РАБОТЕ
Опишите экспериментальную установку и способ проверки уравнения (1).
Получите уравнение 4.
Почему полученный график не проходит через начало координат?
Каким образом можно регулировать момент силы действующий на вращающуюся часть прибора?
Как изменится график зависимости b z (M z), если повторить опыт с гирькой другой массы?






