Изучение образования стоячих волн в закрепленной струне»

Цель работы: Изучить условия образования стоячих волн в закрепленной стру­не. Исследовать зависимость собственных частот от её длины и натяжения.

Вопросы для допуска к работе

1. Уравнение колебательного процесса.
2. Что собой представляет волновой процесс?
3. Уравнение бегущей волны.
4. Чем определяется скорость распространения волны в сплошной среде, в струне?
5. Что наблюдается при распространении волн в ограниченной среде?
6. Что такое стоячая волна?
7. Что называется узлом смещений, пучностью смещений?
8. Чем отличается поперечная волна от продольной? Приведите примеры.

Литература

1. Стрелков С.П. Механика - М.: Наука, 1975, 137-143.

2. Хайкин С.Э. Физические основы механики. – М.: Наука, 1971, 153-155

3. Сивухин Д.В. Курс общей физики. Т.1. Механика - М.: Наука, 1979, 81- 84.

4. Лабораторные занятия по физике. Под ред. Л.Л.Гольдина – М.: Наука, 1983, с. 134-142.

Краткая теория

Рассмотрим гибкую однородную струну, натянутую между двумя неподвижными точками (рис.1). Один конец закреплен в упоре 1, а другой пропущен через упор 2, а затем перекинут через блок и связан с чашечкой с грузами, натягивающими струну.

 

Рис. 1

 

Оттянем струну, а затем отпустим. В струне возникнет бегущая волна. На рис.2 пунктиром изображен элемент струны в какой-то момент времени t, а сплошной линией - в момент времени t+dt. , V - скорость распространения волны.

 

Рис. 2

 

Если проволоку поместить между полюсами магнита З, а по проволоке пропустить ток, то на нее будет действовать сила (сила Ампера), оттягивающая струну. При пропускании тока, изменяющегося по синусоидальному закону, струна будет раскачиваться в соответст­вии с этим законом. В струне возникнет бегущая волна, описываемая уравнением:

, (1)

где x - смещение точек струны от положения равновесия;

, u - частота источника тока, создающего ток в струне (частота генератора).

Картина колебаний в струне создается наложением друг на дру­га бегущими в разные стороны многократно отраженными волнами. При некоторых частотах колебаний картина стабилизируется - в струне возникает стоячая волна, описываемая уравнением:

. (2)

Концы струны закреплены: эти участки струны не смещаются. Поэтому в стоячих волнах, которые могут образоваться в такой струне, этим точкам должны соответствовать узлы стоячей волны. Можно найти ко­ординаты узлов стоячей волны из условия: ;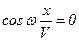

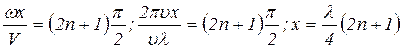. (3)

Из равенства (3) видно, что соседние узлы отстоят друг от друга на расстоянии l/2. Условию (3) соответствуют стоячие волны, изображенные на рис.3:

			3а
			3б
			3в
Рис. 3

Таким образом, стоячие волны могут возбуждаться в струне только на таких частотах (u₀, 2u₀,3u₀), при которых на длине струны укладывается целое число полуволн. Такие частоты называются собст­венными частотами колебаний струны. Частота колебания, при которой на длине струны укладывается одна полуволна, называется основным тоном. Частоты всех остальных стоячих волн называются обертонами. Если частоту возбуждающей переменной силы постепенно изменять, то в струне будут устанавливаться стоячие волны, сперва с частотой u₀, затем 2u₀, а затем 3 u₀ и т.д. При промежуточных частотах колебаний струны практически не будет. Можно сказать, что струна резонирует на частоту u₀, 2u₀,3u₀.

Как видно собственные частоты колебаний за­висят от длины струны и скорости распространения волны в струне. Скорость распространения волны в струне определяется силой натяже­ния F и линейной плотностью r_l.

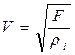, а именно (4)

Задания и указания к их выполнению:

Для проведения эксперимента используется установка, схемати­чески изображенная на рис.1. На струну подается синусоидальное напряжение от звукового генератора ЗГ. Частота силы, раскачивающей струну, равна частоте тока в струне, и может быть измерена по шкале частот звукового генератора.

Задание 1: Получить при некотором постоянном натяжении струны оп­ределенной длины стоячие волны, соответствующие частоте основного тона, первому, второму обертонам.

Установите зажим 2 так, чтобы колеблющийся участок струны имел длину l = 80 - 100 см. Нагрузите струну. Включите ЗГ и спустя 5-10 мин. установите нулевое значение шкалы частот генера­тора (см. указание по паспорту прибора). Перемещая магнит (распо­лагая его на 1/2 l, 1/4 l, 1/6 l от зажима 2) и изменяя частоту генератора, получите стоячие волны, соответствующие виду 3а, Зб, 3в. Снимите показания с шкалы частот генератора.

Задание 2: Исследовать зависимость частоты основного тона при по­стоянном натяжения струны от её длины.

Располагая магнит посередине струны, получите стоячие вол­ны, соответствующе основному тону для различных длин струн. 3апишите показания шкалы частот звукового генератора. По получен­ным данным постройте график: u₀ = u₀(l).

Задание 3: Исследовать зависимость частоты основного тона струны определенной длины от её натяжения.

Расположите магнит посередине струны. Получите стоячие вол­ны, соответствующие основному тону при постоянной длине струны для разных натяжений ее. Запишите показания шкалы частот генера­тора.

По полученным данным рассчитайте скорость распространения волны для разных натяжений струны.

Постройте график зависимости скорости волны от натяжения струны в линеаризованном масштабе. Для выбора функционального масштаба воспользуйтесь равенством (5).

При выполнении задания (3) результаты удобнее представить в виде таблицы

№ п/п	F, Н	u0, Гц	V = u0*l, м/с

 

Для получения зачета необходимо:

1. Уметь демонстрировать резонанс струны.

2. Уметь демонстрировать зависимость собственных частот струны от её длины, натяжения.

3. Представить отчет по стандартной форме.

4. Уметь отвечать на вопросы типа:

Ø Можно ли с помощью уравнения (1) описать колебания, соответствующие продольной волне? Каков смысл всех величин, входящих в это уравнение?

Ø Как происходит отражение волн от закрепленного конца струны?

Ø Можно ли получить резонанс струны на частоте, соответствую­щей первому обертону, если магнит расположен у середины струны?

ЛАБОРАТОРНАЯ РАБОТА № 12