Представить отчет по установленной форме

2. Уметь:

• выводить формулы для периода крутильных колебаний и периода трифилярного подвеса.

• доказывать теорему Штейнера-Тюйгенса.

• вычислять моменты инерции тел правильной геометри­ческой формы.

3. Уметь отвечать на вопросы типа:

• каков физический смысл понятия «момент инер­ции»?

• как определяют момент инерции относительно точки?

• как определяют момент инерции относительно оси вращения?

• может ли масса тела рассматриваться как сосредо­точенная в его центре, если требуется рассчитать момент инерции тела?

• два диска одинаковой массы и толщины сделаны из металлов различных плотностей. Какой из них облада­ет большим моментом инерции?

• в чем состоит свойство аддитивности момента инерции?

 

Работа № 8

«ИЗУЧЕНИЕ ЗАКОНОВ, ЛЕЖАЩИХ В ОСНОВЕ ЯВЛЕНИЯ

ПРЕЦЕССИИ ГИРОСКОПА».

Цель работы: Изучение законов динамики вращательного движения твердо­го тела.

Вопросы для допуска к работе:

1. Что называют гироскопами?

2. Как направлены векторы угловой скорости, углового ускорения?

3. Как направлены векторы момента силы, момента импульса?

4. Основной закон динамики вращательного движения.

5. Что характеризует момент инерции тела и от чего зависит его величина?

6. Как изменится характер вращения тела, если момент внешних сил направлен вдоль оси вращения (оба случая), перпендикулярно этой оси, под углом к ней?

7. Что называют прецессией гироскопа и при каких условиях она возникает?

8. Объясните, почему под действием момента внешних сил, перпендикулярного оси импульсов быстро вращающегося волчка, эта ось начинает совершать вынужденную прецессию?

9. Как связана угловая скорость прецессии с моментом сил?

10. С какой угловой скоростью прецессирует ось симметрии волчка и мгновенная ось вращения?

11. В чем состоит гироскопический эффект и как его объяснить?

12. Где применяется гироскопический эффект?

13. Какие силы называют гироскопическими и какова их природа?

14. Приведите примеры использования гироскопических сил?

Список рекомендуемой литературы:

Савельев И.В. Курс общей физики. – М., т.1, 1962, с. 128-133.

Матвеев А.Н. Механика и теория относительности. - М., 1976, с. 323.

Стрелков С.П. Механика. - М., 1965, с. 214-238.

Хайкин С.Э. Физические основы механики. - М., 1971, с. 446-459.

Краткая теория вопроса:

В основе всей теории гироскопа лежит закон сохранения и изменения момента импульса (момента количества движения).

Рассмотрим гироскоп, состоящий из ротора R, который может вращаться вокруг горизонтальной оси O₁O₂ (рис. 1) и про­тивовеса K. Ось гироскопа шарнирно закреплена в точке O вер­тикальной подставки. Если противовес К расположен таким об­разом, что точка O является центром тяжести, т.е. P₁l₁ = P₂l₂,

Рис. 1

где P₁ - вес ротора, а Р₂ - вес противовеса, то результирующий момент сил, действующих на сис­тему, равен нулю .

Пусть диск вращается с уг­ловой скоростью . В этом случае он обладает моментов ко­личества движения , где J - момент инерции рото­ра относительно оси вращения. Так как на основании II закона динамики для вращательного движения: 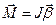или:

, (1)

при : 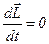, то есть . Это значит, что в этом случае остается постоянным как по величине, так и по направлению, а, следовательно, ось O₁O₂, вдоль кото­рой направлен вектор , будет сохранять свое положение в пространстве неизменным.

Если переместить теперь противовес К вправо, то центр тяжести переместится в точку O` (рис.2), в результате на систему начнет действовать момент сил . В этом слу­чае .(2)

Рис. 2

Величина момента а, следовательно, и зависит как от суммарной силы тяжести, действующей на систе­му, так и от расстояния между точкой закрепления O и новым центром тяжести O`. Это расстояние определяется радиус-вектором , проведенным из точки O в O`. Согласно уравнению (2), направление вектора и вектора должны совпадать. Т.к. в этом случае вектор , а, следовательно, и оси вращения гироскопа, и тогда вектор начнет, не меняя своей величины, поворачиваться. При этом его конец будет двигаться в направлении .

В связи с тем, что вектор будет при этом все время ос­таваться перпендикулярным оси ОО`, эта ось будет все время поворачиваться, описывая конус вокруг вертикальной оси СС₁. Скорость этого вращения называется угловой скоростью прецес­сии , где - угол поворота оси гироскопа во­круг СС₁, за время .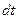

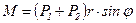Величина момента внешних сил (см. рис.2) рав­на или (3).

Он приложен к точке О, и перпендикулярен плоскости, преходящей через оси ОО` и СС₁.

Найдём величину скорости прецессии . Из формул (2) и (3) получим , но dL (см. рис.2) равна , тогда , откуда или .

Из последнего уравнения видно, что скорость прецессии зависит как от r, так и от скорости вращения волчка w. Если w = const, то отношение 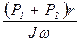должно оставаться неиз­менным при всех значениях r и равным Jw. Отсюда, зная w можно найти момент инерции ротора гироскопа.

Доказать самостоятельно, что r_*(P₁ + P₂) = S_*P₂, где S - величина смещения груза Р₂ из равновесного положения, или S = Dl₂.

В этом случае .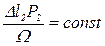

Список заданий:

Задание 1: Исследовать зависимость скорости прецессии гироскопа от положения груза Р₂.

Задание 2: Зная скорость вращения гироскопа (8000 об/мин), найти момент инерции его ротора.

Приборы и приспособления: гироскоп на специальной подставке (рис.3), выпрямитель, умформер для питания гироскопа, секун­домер.

Рис. 3 Гироскоп состоит из следующих частей: М - электромотор, Ш - штанга с делениями, П - противовес с крепящим винтом, Л - неподвижный лимб, Т - треножник, С - пла­та с проводами от умформера к электромотору

Мотор помещен внутри металлического кожуха, скрепленного со штангой. Штанга может вращаться в вертикальной плоскости во­круг оси, проходящей через точку O. Поворот в горизонтальной плоскости достигается благодаря вращению вилки В, на которой крепится стрелка-указатель угла поворота (на рис. 3 не указана).

Гироскоп работает при питании переменным током напряжением 36 В, частотой 400 Гц, поэтому питание его идёт через ум­формер, подключенный к выпрямителю. Время разгона гироскопа 10 минут.

Порядок работы:

1. Перед работой проверить:

а) подключение проводов умформера к гироскопу.

б) подключение проводов умформера к выпрямителю.

2. Умформер ПАГ – 1Ф работает от постоянного тока 3 А нап­ряжением 27 В. На выходе получаем переменный ток 36 В, 0,32 - 0,6 А, частотой 400 Гц.

3. На штанге гироскопа имеется красная полоса - это отметка положения равновесия. Если штанга не находится в положении равновесия, то необходимо добиться его, перемещая противовес П около красной отметки.

4. Включить выпрямитель, подать на умформер постоянный ток 5 А и поддерживать его около двух минут. Ток по мере разгона ум­формера будет падать. Постепенно увеличивать напряжение, пока вольтметр не покажет 26 В. Общий разгон гироскопа равен 10 мин. Ток, употребляемый умформером, должен быть око­ло 3 А.

5. Передвинуть противовес из положения равновесия, например, вправо. По отметкам на штанге находим Dl₂. Штанга начнет вращаться вокруг вертикальной оси. Определим время n - оборотов. Для этого считаем обороты относительно отметки на лимбе и определяем время по секундомеру одновременно. Дан­ные заносим в таблицу.

6. Еще передвинем противовес. Находим Dl^`₂, для этого счита­ем отметки на штанге от красной полосы. Определяем время нескольких оборотов. Данные заносим в таблицу, проделаем вышеуказанное несколько раз.

ЛАБОРАТОРНАЯ РАБОТА № 9