Цель работы: исследовать упругие свойства твердых тел на примерах деформации изгиба и растяжения.
Вопросы для допуска к работе:
- Деформация тела. Виды деформации.
- Закон Гука для различных видов деформации (формулировка и математическая запись).
- Абсолютная и относительная деформации; упругое напряжение.
- Основные характеристики, определяющие упругие свойства материала.
- Ход выполнения работы.
Список рекомендуемой литературы:
- Сивухин Д.В. Общий курс физики. Т.1 - М.: 1979
- Стрелков С.П. Механика. - М.: 1965
- Хайкин С.Э. Физические основы механики. - М.: 1971
Краткая теория:
Деформация представляет собой вид движения, а именно перемещение частей тела относительно друг друга под действием внешней силы. При деформации происходит изменение, как размеров тела, так и его объема.
В общем случае законы, связывающие силы и величину деформаций, сложны. Однако в практически наиболее важных случаях, когда деформации являются малыми, а сами тела упругими (такие деформации называют упругими), силы однозначно определяют деформацию и наоборот.
Несмотря на громадное разнообразие различных видов деформаций, все они могут быть сведены к двум элементарным: однородному растяжению (сжатию) и сдвигу. Кроме элементарных принято выделять также и сложные виды деформаций: кручение и изгиб.
Деформацией растяжения или сжатия называется деформация, связанная с относительным изменением длины деформируемого образца. Если материал образца однороден, то все участки его будут деформированы одинаково при действии на него некоторой однородной нагрузки. Такую деформацию характеризуют относительной деформацией e:
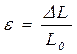 (1)
(1)
где: DL - изменение длины деформируемого участка, имевшего первоначальную длину L0. Величину усилия, действующего на единицу площади поперечного сечения образца, называют упругим напряжением и обозначают d. Напряжение, возникающее в деформируемом образце, равно:
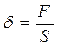 (2)
(2)
Упругая деформация достаточно точно описывается законом Гука:
 , (3)
, (3)
где Е - модуль Юнга, который характеризует упругие свойства твердых тел при деформации «растяжения — сжатия». Он численно равен величине упругого напряжения, при условии, что относительное удлинение образца равно единице. Закон Гука справедлив лишь для идеально упругих тел, а не для реальных тел. Если вдоль всего образца величина абсолютного удлинения одинакова, то такую деформацию называют однородной.
Деформация изгиба является примером неоднородной деформации. Это связано с тем, что при этом типе деформации, одни слои сжимаются, а другие, наоборот, растягиваются. При этом следует отметить, что величина деформации образца зависит от способа его закрепления.
Для экспериментального определения модуля Юнга при изучении деформации изгиба, чаще всего пользуются сосредоточенной нагрузкой, когда действующая сила приложена к определенной точке. При деформации изгиба величиной, характеризующей деформацию, является стрела прогиба l. Величина прогиба зависит от величины нагрузки, формы и размеров образца, а также модуля Юнга. Если испытуемый образец имеет форму бруска, то при действии сосредоточенной нагрузки на образец, стрела прогиба связана с геометрическими размерами образца, модулем Юнга и действующей силой, следующим образом:
 , (4)
, (4)
где b - ширина образца, h - высота образца, L - длина образца между точками опоры, k. - коэффициент пропорциональности, зависящий от способа закрепления. Для бруска, свободно лежащего на опорах, k=1/4. Из формулы (4) следует, что модуль Юнга можно определить, воспользовавшись выражением:
 . (5)
. (5)
Задания и указания к их выполнению:
Задание 1: Определение модуля Юнга по прогибу стержня сосредоточенной нагрузкой.
Для определения модуля Юнга при выполнении данного задания используется установка схема, которой приведена на рис. 1.
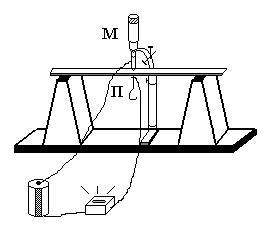
|
| Рис. 1 |
В данном случае образец, в виде бруска, свободно опирается на две призмы. Изменяя нагрузку, действующую на образец, производят измерение величины стрелы прогиба l. Величина прогиба измеряется с помощью микрометра, снабженного электрическим индикатором контакта. По загоранию индикаторной лампочки можно судить о наличии соприкосновения микрометра с поверхностью образца. Однако отсчет микрометра, соответствующий моменту замыкания цепи, не вполне точен, так как рука может продолжать вращать винт микрометра и после достижения контакта. Поэтому рекомендуется брать среднее из двух показаний: при замыкании и размыкании цепи. Для более точного отсчета, образец предварительно нагружают массой 0,5 кг, которую в дальнейшем не учитывают. Нагрузка изменяется путем увеличения числа грузов, помещаемых на площадку.
При выполнении данного задания снимают зависимость величины стрелы прогиба от внешней нагрузки и строят график, по которому определяют модуль Юнга. Рекомендуется снимать значения стрелы прогиба, как в прямом, так и в обратном (снимая грузы) направлениях. Результаты эксперимента занести в таблицу.
Задание 2: Определение модуля Юнга методом двух подвесов.
При выполнении данного задания величину абсолютной деформации определяют из сравнения длин проволок, которые подвергнуты различному воздействию. Схема экспериментальной установки приведена на рис.3

|
| Рис. 3 |
Из рисунка видно, что проволоки первоначально имеют одинаковую длину. Между проволоками расположен уровень М, который укреплен на рамке, связанной с концами проволок АВ и CD. Один конец уровня опирается на микрометрический винт. Если к проволоке АВ подвесить груз, то она под действием этого груза деформируется и при этом пузырек уровня сместится из соответствующего положения равновесия. Для возвращения уровня в положение равновесия, необходимо вращением винта микрометра вернуть пузырек в исходное положение. Разность показаний и даст значение величины абсолютной деформации.
Перед началом измерения проволоки необходимо выпрямить, для чего к ним подвешивают грузы массой 1 кг, которые во время выполнения работы не снимают, и, вращая винт микрометра, пузырек устанавливают посередине. Затем нагружают проволоку АВ (m = 1,2,3 кг).
Проволока АВ удлиняется и нарушается равновесие уровня М. Длина проволоки АВ и CD равна 2350  1 мм.
1 мм.
После выполнения задания все грузы обязательно необходимо снять.
Для получения зачета необходимо:
- Представить отчет по установленной форме.
2. Уметь отвечать на вопросы типа:
• Каков физический смысл модуля Юнга? Единицы измерения.
• Показать графически зависимость деформации от напряжения и указать область напряжений, в которой имеет место Закон Гука.
• Пользуясь диаграммой указать область пластической деформации, область текучести материала, область, соответствующую пределу прочности материала.
• Изобразить графически вид кривых «напряжение-деформация» для пластических и хрупких тел.
• Перечислить разновидность деформаций и записать закон Гука для каждой из них.
• Вывести формулу энергии упругой деформации для случая деформации растяжения (сжатия).
• Физический смысл коэффициента Пуассона. Чему равно максимальное значение коэффициента Пуассона?
• Записать формулу, связывающую модуль Юнга с модулем сдвига.
ЛАБОРАТОРНАЯ РАБОТА №10
«ОПРЕДЕЛЕНИЕ СКОРОСТИ РАСПРОСТРАНЕНИЯ ЗВУКОВЫХ ВОЛН В ВОЗДУХЕ И ТВЕРДЫХ ТЕЛАХ»
Цель работы: Изучение закономерностей распространения колебательных процессов в упругих средах.
Вопросы для допуска к работе
1. Что представляет собой волновой процесс?
2. Чем отличается распространение волн в неограниченных и ограниченных средах.
3. Что такое стоячая волна, её длина?
4. Какими способами можно определить длину волны в среде?
5. В чём заключается смысл способа определения скорости звука в воздухе по Квинке?
6. Опишите способ определения скорости звука в воздухе методом сложения взаимно перпендикулярных колебаний.
Литература
1. Савельев И.В. Курс общей физики. - М., т.1, 1962, с. 209-235.
2. Архангельский М.М. Курс физики. Механика. – 1973, с.319 -327
3. Стрелков С.П. Механика. - М., 1965, с. 459-489.
4. Ландсберг Г.С. Элементарный учебник физики. - М., т.III, 1962, с. 79 - 115.
Сведения из теории






