Выведите этот результат самостоятельно)

Изложенные выше рассуждения были сделаны при допущении, что кроме упругих или квазиупругих сил никакие силы на материальную точку не действуют. На практике всякое колебание си­стемы, которое не поддерживается извне, затухает, амплитуда ее колебания с течением времени уменьшается. Причина затуха­ния обусловливается силами, тормозящими движение. При учёте этих сил в уравнение движения необходимо добавить слагаемое, определяющее величину сил сопротивления.

Рассмотрим случай колебания в вязкой среде. Будем считать, что скорости не слишком велики, поэтому , где r - коэффициент сопротивления. Тогда уравнение движения мо­жет быть написано в виде: ( 4 ). Введем обозначения . Тогда уравнение (4) примет вид:

. ( 5 )

Решение уравнения (5), описывающее движение материаль­ной точки под действием упругой или квазиупругой силы в среде с сопротивлением, имеет вид: , или , где ( 6 ) - амплитуда, уменьшающаяся с течением времени, а , или ( 7 ). Период колебания в среде с сопротивлением больше, чем период колебания точки такой же массы m под действием такой же упругой или квазиупругой силы в среде без сопротивления.

Логарифм отношения двух последовательных значений ампли­туд, отстоящих друг от друга на время, равное периоду Т, на­зывается логарифмическим декрементом затухания:

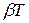=. . ( 8 )

Если взять несколько колебаний, то , а . При (e = 2,718), Nl = 1.

Таким образом, величина обратная декременту l, равна числу колебаний, через которое амплитуда колебаний уменьшит­ся в e раз.

Зная l, можно, пользуясь соотношением определить коэффициент сопротивления r.

Для характеристики колеблющейся системы часто применяется величина Q, называемая добротностью. Эта величина представляет собой умноженное на 2p отношение запасенной энергии к среднему значению энергии, теряемому за один период (при незначительном затухании). Можно показать, что доброт­ность связана с логарифмическим декрементом затухания следую­щим соотношением: . ( 9 )

Рассмотрим примеры гармонических колебательных движений.

Пример I. Определение периода колебаний физического маятника.

Физическим маятником называется твер­дое тело, которое может качаться вокруг неподвижной горизон­тальной оси. Точка пересечения её с вертикальной плоскостью, проходящей через центр масс маятни­ка С, называется точкой подвеса маятника (рис.1).

Рис.1

Положение тела в любой момент времени можно охарак­теризовать углом отклонения его из положения равновесия j. Рассмот­рим решение при малых углах отклонения.

Силу тяжести mg можно счи­тать приложенной к центру масс С. Момент составляющей силы тяжести сообщает телу угловое ускорение , равное , ( 10 )

где J - момент инерции тела относительно оси 0. Подставив в (10) выражения для b и (при малых углах откло­нения), получим: . Это уравнение вполне аналогич­но уравнению (1). Откуда мы получаем: при малых углах отклоне­ния тело будет совершать около положения равновесия гармоническое колебательное движение с циклической частотой и периодом

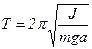( 11 ).

Колебания физического маятника изохронны (период колеба­ний не зависит от амплитуды), когда угловая амплитуда колебаний не превышает несколько градусов. При больших амплитудах изохронность нарушается.

Пример 2: Определение периода колебаний математического маятника.

Математическим называется маятник, вся масса которого практически сосредоточена в одной точке - в центре масс маятника С. Примером математического маятника мо­жет служить шарик, подвешенный на длинной нити.

Математический маятник можно рассматривать как частный случай физического маятника: a = l, 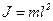где l - длина маятника. Тогда формула (11) переходит в . ( 12)

Сравнивая формулы (11) и (12), заключаем, что физичес­кий маятник колеблется с таким же периодом, как математичес­кий маятник с длиной (13), которая называется при­веденной длиной физического маятника.

Задания

Задание 1. Определить ускорение силы тяжести (свободного падения) при помощи математического маятника.

Указания к выполнению задания:

- Напишите формулу для определения " g " с помощью математи­ческого маятника и оцените точность измерения.

- Изменить длину маятника на 15 -20 см (изменение длины маятника измеряется по шкале на стойке установки) и вновь произвести измерения периода колебаний для маятника новой длины.

Покажите, что в этом случае "g" можно рассчитать по формуле , где - изменение длины маятника. Оцените (предварительно) ошибку измерения "g" данным методом.

- Составьте таблицу для записи результатов измерений, а измерения периода для каждой длины повторять не менее трех раз.

- Комбинируя результаты измерений и периодов колебаний, получите несколько значений "g". Определите ошибку Dg измерения ускорения силы тяжести данным методом.

Задание 2. Рассчитать массу груза, который необходимо положить на площадку, чтобы период колебаний пружинного маятника был равен Т. (Т лежит в интервале от 0,5 до 2,0 с).

Задание 3. С помощью самописца записать график затухающих колебаний и определить:

Ø Логарифмический декремент затухания;

Ø Коэффициент затухания;

Ø Период затухающих и свободных колебаний;

Ø Добротность колебательной системы;

Ø Записать уравнение затухающих колебаний.

Задание 4. Рассчитать период колебаний физического маятника. Результат расчета проверить экспериментально.

Указание. Момент инерции физического маятника состоящего из стержня и диска, можно определить, применяя теорему Штейнера-Гюйгенса.

Вопросы для полу­чения зачёта:

1. Сравнить время прохождения колеблющейся точкой первой и второй половин амплитуды.

2. Какова должна быть длина математического маятника, чтобы его период равнялся 1 секунде?

3. Амплитуда колебаний имеющегося в лаборатории математичес­кого маятника 2 см.

– Значение каких величин, характеризующих движение этого маятника (смещение, период, частота, циклическая частота, фа­за, скорость, ускорение), являются постоянными?

– Определите тангенциальное ускорение маятника в крайних положениях и положении равновесия.

– Оцените величину механической энергии маятника при про­хождении его через положение равновесия.

– При каких предположениях справедливы полученные ответы? Как повлияет на ответы учёт тех факторов, которыми вы пренебрегли?

– Как изменится механическая энергия маятника, если амплитуду увеличить в два раза?

4. При каких условиях справедливы выражения (11) и (12) для периодов физического и математического маятников?

5. Что называется приведенной длиной физического маятника, от чего она зависит?

6. От чего зависит точность определения периодов колебаний?

7. Как будет зависеть точность определения ускорения силы тяжести с помощью математических маятников разной длины, от выбора их длин и разности длин?

8. Как изменится период колебаний, если маятник находится на Луне; если под маятником расположить магнит?

ЛАБОРАТОРНАЯ РАБОТА № 6