Основные формулы и законы
· Момент инерции материальной точки
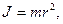
где m — масса точки; r — расстояние до оси вращения.
· Момент инерции системы (тела) относительно неподвижной оси
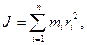
где 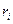 - расстояние материальной точки массой
- расстояние материальной точки массой 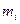 до оси вращения; в случае непрерывного распределения масс
до оси вращения; в случае непрерывного распределения масс
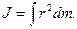
· Моменты инерции тел правильной геометрической формы (тела считаются однородными; m — масса тела):
| Тело | Положение оси вращения | Момент инерции |
| Полый тонкостенный цилиндр радиусом R | Ось симметрии | 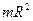
|
| Сплошной цилиндр или диск радиусом R | Ось симметрии | 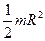
|
| Прямой тонкий стержень длиной l | Ось перпендикулярна стержню и проходит через его середину | 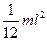
|
| Прямой тонкий стержень длиной l | Ось перпендикулярна стержню и проходит через его конец | 
|
| Шар радиусом R | Ось проходит через центр шара | 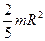
|
· Теорема Штейнера
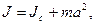
где 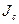 - момент инерции тела относительно оси, проходящей через центр масс; J - момент инерции относительно параллельной оси, отстоящей от первой на расстоянии а; m - масса тела.
- момент инерции тела относительно оси, проходящей через центр масс; J - момент инерции относительно параллельной оси, отстоящей от первой на расстоянии а; m - масса тела.
· Кинетическая энергия тела, вращающегося вокруг неподвижной оси z
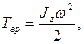
где 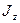 - момент инерции тела относительно оси z;
- момент инерции тела относительно оси z; 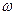 - его угловая скорость.
- его угловая скорость.
· Кинетическая энергия тела, катящегося по плоскости без скольжения,
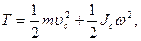
где m - масса тела; 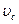 - скорость центра масс тела;
- скорость центра масс тела; 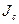 - момент инерции тела относительно оси, проходящей через его центр масс;
- момент инерции тела относительно оси, проходящей через его центр масс; 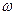 - угловая скорость тела.
- угловая скорость тела.
· Момент силы относительно неподвижной точки
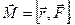
где r - радиус-вектор, проведенный из этой точки в точку приложения силы 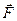 . Модуль момента силы относительно неподвижной оси
. Модуль момента силы относительно неподвижной оси
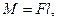
где l - плечо силы (кратчайшее расстояние между линией действия силы и осью вращения).
· Работа при вращательном движении тела
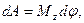
где 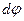 - угол поворота тела;
- угол поворота тела; 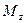 - момент силы относительно оси z.
- момент силы относительно оси z.
· Момент импульса (момент количества движения) твердого тела относительно оси вращения
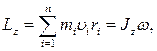
где 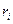 - расстояние от оси z до отдельной частицы тела;
- расстояние от оси z до отдельной частицы тела; 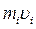 - импульс этой частицы;
- импульс этой частицы; 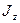 - момент инерции тела относительно оси z;
- момент инерции тела относительно оси z; 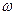 - его угловая скорость.
- его угловая скорость.
· Уравнение (закон) динамики вращательного движения твердого тела относительно неподвижной оси
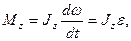
где 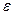 - угловое ускорение;
- угловое ускорение; 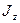 - момент инерции тела относительно оси z.
- момент инерции тела относительно оси z.
· Закон сохранения момента импульса для замкнутой системы
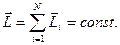
3.1. Определите момент инерции сплошного однородного диска радиусом 40 см и массой 1 кг относительно оси, проходящей через середину одного из радиусов перпендикулярно плоскости диска.
A. [0,12 кг×м2] B. [1,2 кг×м2]
C. [12 кг×м2] D. [0,012 кг×м2]
3.2. Определите момент инерции тонкого однородного стержня длиной 50 см и массой 360 г относительно оси, перпендикулярной стержню и проходящей через: 1) конец стержня; 2) точку, отстоящую от конца стержня на 1/6 его длины.
A. [1) 3×10-2 кг×м2; 2) 1,75×10-2 кг×м2] B. [1) 3 кг×м2; 2) 1,75 кг×м2]
C. [1) 0,3×10-2 кг×м2; 2) 1,75×10-2 кг×м2] D. [1) 3 кг×м2; 2) 175 кг×м2]
3.3. Вертикальный столб высотой 5 м подпиливается у основания и падает на землю. Определите линейную и угловую скорости его верхнего конца в момент удара о землю.
А. [12 м/с; 2,4 рад/с] В. [17,1 м/с; 3,4 рад/с]
С. [2,4 м/с; 12 рад/с] D. [ 24,2 м/с; 4,8 рад/с]
3.4. Шар и сплошной цилиндр одинаковой массы, изготовленные из одного и того же материала, катятся без скольжения с одинаковой скоростью. Определите, во сколько раз кинетическая энергия шара меньше кинетической энергии сплошного цилиндра.
A. [В 1,07 раза] B. [В 2,07 раза]
C. [В 7 раз] D. [В 10,7 раза]
3.5. Сравните полную кинетическую энергию обруча, скользящего вдоль наклонной плоскости, и полную кинетическую энергию обруча, катящегося по наклонной плоскости.
А. [2] В. [3]
С. [1] D. [1/2]
3.6. Полная кинетическая энергия диска, катящегося по горизонтальной поверхности, равна 24 Дж. Определите кинетическую энергию поступательного и вращательного движения диска.
A. [Т1 = 16 Дж, Т2 = 8 Дж] B. [Т1 = 1,6 Дж, Т2 = 8 Дж]
C. [Т1 = 1,6 Дж, Т2 = 0,8 Дж] D. [Т1 = 16 Дж, Т2 = 0,8 Дж]
3.7. К ободу однородного сплошного диска массой 10 кг, насаженного на ось, приложена постоянная касательная сила 30 Н. Определите кинетическую энергию диска через время 4 с после начала действия силы.
A. [1,44 кДж] B. [14,4 кДж]
C. [14,4 Дж] D. [1,44 Дж]
3.8. Шар радиусом 10 см и массой 5 кг вращается вокруг оси симметрии согласно уравнению 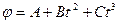 (В = 2 рад/с2, С = -0,5 рад/с3). Определите момент сил для t = 3 с.
(В = 2 рад/с2, С = -0,5 рад/с3). Определите момент сил для t = 3 с.
A. [ -0,1 Н×м] B. [0,2 Н×м]
C. [ -0,3 Н×м] D. [0,3 Н×м]
3.9. Через неподвижный блок в виде однородного сплошного цилиндра массой 160 г перекинута невесомая нить, к концам которой подвешены грузы массами 200 г и 300 г. Пренебрегая трением в оси блока, определите: 1) ускорение грузов; 2) силы натяжения Т 1 и Т 2 грузов.
A. [1) 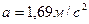 ;
; 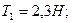
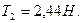 ]
]
B. [1) 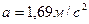 ;
; 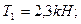
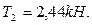 ]
]
C. [1) 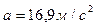 ;
; 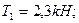
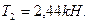 ]
]
D. [1) 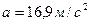 ;
; 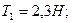
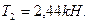 ]
]
3.10. Вентилятор вращается с частотой 600 об/мин. После выключения он начал вращаться равнозамедленно и, сделав 50 оборотов, остановился. Работа сил торможения равна 31,4 Дж. Определите: 1) момент сил торможения; 2) момент инерции вентилятора.
A. [1) 0,1 Н×м; 2) 15,9 кг×м2] B. [1) 0,1 кН×м; 2) 159 кг×м2]
C. [1) 0,1 кН×м; 2) 15,9 кг×м2] D. [1) 1 Н×м; 2) 159 кг×м2]
3.11. Маховик в виде сплошного диска, момент инерции которого 150 кг×м2, вращается с частотой 240 об/мин. Через время t = 1 мин, как на маховик стал действовать момент сил торможения, он остановился. Определите: 1) момент сил торможения; 2) число оборотов маховика от начала торможения до полной остановки.
A. [1) 62,8 Н×м; 2) 120] B. [1) 62,8 Н×м; 2) 1200]
C. [1) 62,8 кН×м; 2) 120] D. [1) 62,8 кН×м; 2) 1200]
3.12. По горизонтальной плоской поверхности катится диск со скоростью 8 м/с. Определите коэффициент сопротивления, если диск, будучи предоставленным самому себе, остановился, пройдя путь 18 м.
А. [0,27] В. [0,18]
С. [0,10] D. [0,36]
3.13. Сплошной однородный диск скатывается без скольжения по наклонной плоскости, образующей угол b с горизонтом. Определите линейное ускорение центра диска.
A. [ 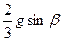 ] B. [
] B. [  ]
]
C. [ 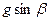 ] D. [
] D. [ 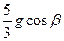 ]
]
3.14. С наклонной плоскости, составляющей угол α с горизонтом, скатывается шар. С каким ускорением движется центр шара?
А. [ 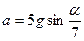 ] В. [
] В. [ 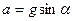 ]
]
С. [ 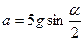 ] D. [
] D. [ 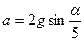 ]
]
3.15. Шар скатывается с наклонной плоскости высотой 90 см. Какую линейную скорость будет иметь центр шара в тот момент, когда шар скатится с наклонной плоскости?
А. [3,5 м /с] В. [35,5 м /с]
С. [4,24 м /с] D. [42,4 м /с]
3.16. К ободу однородного сплошного диска радиусом 0,5 м приложена постоянная касательная сила 100 Н. При вращении диска на него действует момент сил трения 2 Н×м. Определите массу диска, если известно, что его угловое ускорение постоянно и равно 16 рад/с2.
A. [24 кг] B. [2,4 кг]
C. [0,24 кг] D. [48 кг]
3.17. Частота вращения маховика, момент инерции которого равен 120 кг×м2, составляет 240 об/мин. После прекращения действия на него вращающего момента маховик под действием сил трения в подшипниках остановился за время t = 3,14 мин. Считая трение в подшипниках постоянным, определите момент сил трения.
A. [16 Н×м] B. [1,6 Н×м]
C. [16 кН×м] D. [32 Н×м]
3.18. Маховик в виде сплошного диска, момент инерции которого 1,5 кг×м2, вращаясь при торможении равнозамедленно, за время t = 1 мин уменьшил частоту вращения с 240 об/мин до 120 об/мин. Определите: 1) угловое ускорение маховика; 2) момент силы торможения; 3) работу торможения.
A. [1) 0,21 рад/с2, 2) 0,315Н×м;3) 355Дж]
B. [1) 0,21 рад/с2, 2) 0,315кН×м;3) 355кДж]
C. [1) 21 рад/с2, 2) 0,315Н×м;3) 355Дж]
D. [1) 21 рад/с2, 2) 0,315кН×м;3) 355кДж]
3.19. С наклонной плоскости, составляющей угол 30° к горизонту, скатывается без скольжения шарик. Пренебрегая трением, определите время движения шарика по наклонной плоскости, если известно, что его центр масс при скатывании понизился на 30 см.
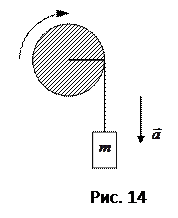 A. [0,585 с] B. [5,85 с]
A. [0,585 с] B. [5,85 с]
C. [58,5 с] D. [585 с]
3.20. На однородный сплошной цилиндрический вал (рис. 14) радиусом 50 см намотана легкая нить, к концу которой прикреплен груз массой 6,4 кг. Груз, разматывая нить, опускается с ускорением 2 м/с2. Определите: 1) момент инерции вала; 2) массу вала.
A. [1) 6,25 кг×м2; 2) 50 кг]
B. [1) 62,5 кг×м2; 2) 50 кг]
C. [1) 6,25 кг×м2; 2) 5 кг]
D. [1) 62,5 кг×м2; 2) 5 кг]
3.21. Через неподвижный блок в виде однородного сплошного цилиндра массой 0,2 кг перекинута невесомая нить, к концам которой прикреплены тела массами 0,35 кг и 0,55 кг. Пренебрегая трением в оси блока, определите: 1) ускорение грузов; 2) отношение Т 2/ Т 1 сил натяжения нити.
A. [1) 1,96 м/с2; 2) 1,05] B. [1) 19,6 м/с2; 2) 10,5]
C. [1) 19,6 м/с2; 2) 2,05] D. [1) 19,6 м/с2; 2) 10,05]
3.22. Для демонстрации законов сохранения применяется маятник Максвелла, представляющий собой массивный диск радиусом R и массой m, туго насаженный на ось радиусом r, которая подвешивается на двух предварительно намотанных на нее нитях (рис. 15). Когда маятник отпускают, то он совершает возвратно-поступательное движение в вертикальной плоскости при одновременном вращении диска вокруг оси. Не учитывая сил сопротивления и момента инерции оси, определите: 1) ускорение поступательного движения маятника; 2) силу натяжения нити.
A. [1) 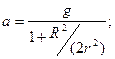 2)
2) 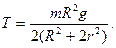 ]
]
B. [1) 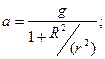 2)
2) 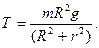 ]
]
C. [1) 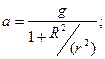 2)
2) 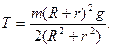 ]
]
D. [1) 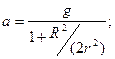 2)
2) 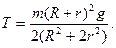 ]
]
3.23. Шар массой 3 кг катится со скоростью 2 м/с и сталкивается с покоящимся шаром массой 5 кг. Какая работа будет совершена при деформации шаров? Удар считать абсолютно неупругим, прямым, центральным.
А. [- 6,15 Дж] В. [6,15 Дж]
С. [- 3,75 Дж] D. [3,75 Дж]
3.24. Шар массой 1 кг, катящийся без скольжения, ударяется о стенку и откатывается от нее. Скорость шара до удара о стенку 10 см/с, после удара 8 см/с. Найти: 1) количество теплоты, выделившееся при ударе; 2) импульс, который получает стенка.
А. [2,52 мДж; 0,18 кг·м/с] В. [2,52 мДж; 0,02 кг·м/с]
С. [25,2 Дж; 18 кг·м/с] D. [25,2 Дж; 2 кг·м/с]
3.25. Медный шар радиусом 10 см вращается со скоростью, соответствующей частоте 2 об/с, вокруг оси, проходящей через его центр. Какую работу надо совершить, чтобы увеличить угловую скорость вращения вдвое?
А. [34,1 Дж] В. [341 Дж]
С. [34,1 кДж] D. [34,1 мДж]
3.26. Деревянный стержень массой 1 кг и длиной 40 см может вращаться вокруг оси, проходящей через его середину перпендикулярно к стержню. В конец стержня попадает пуля массой 10 г, летящая перпендикулярно к оси и стержню со скоростью 200 м/с. Определите угловую скорость, которую получит стержень, если пуля застрянет в нем.
А. [29 рад/с] В.[967 рад/с]
С. [9,677 рад/с] D.[0,29 рад/с]
3.27. Два маленьких шарика массами 40 г и 120 г соответственно соединены стержнем длиной 20 см, масса которого ничтожно мала. Система вращается около оси, перпендикулярной к стержню и проходящей сквозь центр инерции системы. Определить импульс и момент импульса системы. Частота оборотов равна 3 с-1.
А. [0; 2,3·10-2 кг·м/с] В. [0; 23 кг·м/с]
С. [0; 230 кг·м/с] D. [0; 11,3·10-2 кг·м/с]
3.28. Какую работу нужно произвести, чтобы увеличить частоту оборотов маховика от 0 до 120 мин-1? Массу маховика, равную 0,5 т можно считать распределенной по ободу диаметром 1,5 м. Трением пренебречь.
А. [22,2 кДж] В. [79,9 МДж]
С. [79,9 кДж] D. [22,2 Дж]
3.29. На скамье Жуковского (вращающаяся платформа без трения) стоит человек и держит в руках стержень по оси скамьи. Скамья с человеком вращается с угловой скоростью 4 рад/с. С какой скоростью будет вращаться скамья с человеком, если стержень повернуть так, чтобы он занял горизонтальное положение? Суммарный момент инерции человека и скамьи 5 кг·м2, длина стержня 2 м, масса 6 кг. Считать, что центр масс стержня с человеком в обоих случаях находится на оси платформы.
А. [2,9 рад/с.] В. [4 рад/с]
С. [10 рад/с] D. [0,35 рад/с]
3.30. На неподвижной скамье Жуковского стоит человек и держит в руке за ось велосипедное колесо, вращающееся вокруг своей оси с угловой скоростью 25 рад/с. Ось колеса расположена вертикально и совпадает с осью скамьи. С какой скоростью станет вращаться скамья, если повернуть колесо вокруг горизонтальной оси на угол 90°? Момент инерции человека и скамьи равен 2,5 кг·м2, момент инерции колеса 0,5 кг·м2.
А. [5 рад/с] В. [4,2 рад/с]
С. [50 рад/с] D. [42 рад/с]
3.31. Платформа в виде диска вращается по инерции без трения около вертикальной оси с частотой 14 мин-1. На краю платформы стоит человек. Когда человек перешел в центр платформы, частота возросла до 25 мин-1. Масса человека 70 кг. Определите массу платформы. Момент инерции человека рассчитывать, как для материальной точки.
А. [178 кг] В. [89 кг]
С. [159 кг] D. [318 кг]
3.32. Горизонтальная платформа массой 150 кг вращается вокруг вертикальной оси, проходящей через центр платформы с частотой 8 мин-1. Человек массой 70 кг стоит при этом на краю платформы. С какой угловой скоростью начнет вращаться платформа, если человек перейдет от края платформы к ее центру? Считать платформу круглым однородным диском, а человека - материальной точкой.
А. [1,62 рад/с] В. [97 рад/с]
С. [3,24 рад/с] D. [73,7 рад/с]
3.33. На краю неподвижной скамьи Жуковского диаметром 0,8 м и массой 6 кг стоит человек массой 60 кг. С какой угловой скоростью начнет вращаться скамья, если человек поймает летящий на него мяч массой 0,5 кг? Траектория мяча горизонтальна и проходит на расстоянии 0.4 м от оси скамьи. Скорость мяча 5 м/с.
А. [0,1 рад/с] В. [0,16 рад/с]
С. [0,05 рад/с] D. [0,4 рад/с]
3.34*. Платформа в виде диска диаметром 3 м и массой 180 кг может вращаться вокруг вертикальной оси. С какой угловой скоростью будет вращаться эта платформа, если по ее краю пойдет человек массой 70 кг со скоростью 1,8 м/с относительно платформы? [0,53 рад/с]
3.35*. В центре вращающегося столика стоит человек, держащий на вытянутых руках на расстоянии 150 см друг от друга две гири. Столик вращается с частотой 1 с-1. Человек сближает гири до расстояния 80 см, и частота увеличивается до 1,5 с-1. Определите работу, произведенную человеком, если каждая гиря имеет массу 2 кг. Момент инерции человека относительно оси столика считать постоянным.
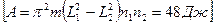
Механические колебания
Основные формулы
· Уравнение гармонических колебаний:
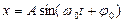 ,
,
где 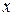 – смещение точки от положения равновесия, А – амплитуда колебаний, w 0– круговая (циклическая частота), t – время,
– смещение точки от положения равновесия, А – амплитуда колебаний, w 0– круговая (циклическая частота), t – время, 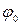 – начальная фаза колебаний.
– начальная фаза колебаний.
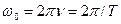 ,
,
где n – частота колебаний, Т – период колебаний.
· Скорость и ускорение при гармонических колебаниях:
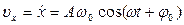 ,
,
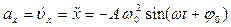 .
.
· Возвращающая сила
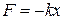 ,
,
где 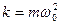 – коэффициент упругой (квазиупругой) силы, m – масса материальной точки.
– коэффициент упругой (квазиупругой) силы, m – масса материальной точки.
· Полная энергия при гармонических колебаниях:
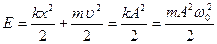 .
.
· Периоды колебаний:
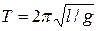 – математический маятник (
– математический маятник (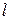 – длина нити),
– длина нити),
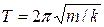 – пружинный маятник (m – масса тела,
– пружинный маятник (m – масса тела, 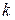 – коэффициент жесткости),
– коэффициент жесткости),
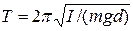 – физический маятник (I – момент инерции тела относительно оси, проходящей через точку подвеса, m – масса тела, d – расстояние от точки подвеса до центра масс).
– физический маятник (I – момент инерции тела относительно оси, проходящей через точку подвеса, m – масса тела, d – расстояние от точки подвеса до центра масс).
· Уравнение затухающих колебаний:
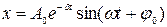 ,
,
где 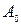 – амплитуда колебаний в начальный момент времени,
– амплитуда колебаний в начальный момент времени,  – коэффициент затухания.
– коэффициент затухания.
· Амплитуда результирующего колебания, полученного при сложении двух колебаний одинаковой частоты и одного направления:
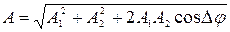 ,
,
где 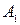 и
и 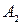 - амплитуды слагаемых колебаний,
- амплитуды слагаемых колебаний, 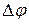 - разность фаз слагаемых колебаний.
- разность фаз слагаемых колебаний.
· Начальная фаза результирующего колебания определяется из формулы:
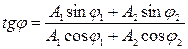 .
.
· Уравнение траектории точки, участвующей в двух взаимноперпендикулярных колебаниях с одинаковыми частотами:
 .
.
4.1. Записать уравнение гармонических колебаний точки с амплитудой 5 см, если за 2 минуты совершается 120 колебаний, а начальная фаза равна 60º.
А. [ 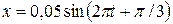 м] В. [
м] В. [ 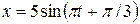 м]
м]
С. [ 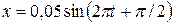 м] С. [ x =
м] С. [ x = 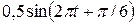 м]
м]
4.2. Точка совершает гармонические колебания с периодом 8 с и начальной фазой, равной нулю. Определите, за какое время точка сместится от положения равновесия на половину амплитуды.
А. [4/3 c] B. [1 c] C. [2/3 c] D. [1/3 c]
4.3. Определите максимальные значения скорости и ускорения точки, совершающей гармонические колебания с амплитудой 2 см и периодом 2 с.
A.[0,0628 м/c; 0,197 м/ 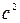 ] B.[0,0314 м/с; 0,394 м/
] B.[0,0314 м/с; 0,394 м/ 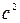 ]
]
С.[0,197 м/с; 0,0628 м/ 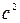 ] D.[0,125 м/с; 0,788 м/
] D.[0,125 м/с; 0,788 м/ 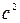 ]
]
4.4. Точка совершает гармонические колебания с периодом 12 с. Определите, за какое время скорость точки увеличится от нуля до половины максимального значения.
A.[1 c] B.[1,5 c] C.[2 c] D.[2,5 c]
4.5. Точка совершает гармонические колебания с периодом 12 c. Определите, за какое время ускорение точки увеличится от нуля до половины максимального значения.
A.[1 c] B.[2 c] C.[3 c] D.[4 c]
4.6. Уравнение движения точки дано в виде 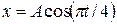 . Определите моменты времени, при которых достигается максимальная скорость точки.
. Определите моменты времени, при которых достигается максимальная скорость точки.
A.[2с, 6с, 10с …] B.[1с, 5, 9с …] C.[3с, 7с, 11с …] D.[4с, 8с, 12с …]
4.7. Уравнение движения точки дано в виде 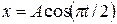 . Определите моменты времени, при которых достигается максимальное ускорение точки.
. Определите моменты времени, при которых достигается максимальное ускорение точки.
A.[0c, 2c, 4c …] B.[1c, 3c, 5c …] C.[2c, 4c, 6c …] D.[3c, 5c, 7c …]
4.8. Как изменится частота колебаний груза, висящего на двух одинаковых пружинах, если от их последовательного соединения перейти к параллельному?
A.[увеличится в 2 раза] B.[уменьшится в 2 раза]
С.[увеличится в 4 раза] D.[не изменится]
4.9. Материальная точка совершает гармонические колебания согласно уравнению 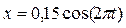 м. Определите максимальное значение модуля возвращающей силы и полную энергию точки, если её масса 0,1 кг.
м. Определите максимальное значение модуля возвращающей силы и полную энергию точки, если её масса 0,1 кг.
A.[0,59 Н; 0,047 Дж] B.[5,9 Н; 0,47 Дж]
С.[0,059 Н; 0,47 Дж] D.[11,8 Н; 0,094 Дж]
4.10. Определите отношение кинетической энергии точки, совершающей гармонические колебания, к её потенциальной энергии для моментов времени: a) t=T /12; б) t=T /8; в) t=T /6, где Т – период колебаний. Начальная фаза равна нулю.
A.[3; 1; 1/3] B.[1/3; 1; 3] C.[1; 3; 1/3] D.[1; 1/3; 3]
4.11. Определите отношение кинетической энергии точки, совершающей гармонические колебания, к её потенциальной энергии для моментов времени, при которых смещение от положения равновесия составляет: а) х=А /4; б) х=А /2; в) х=А, где А – амплитуда колебаний.
A.[15; 3; 0] B.[0; 3; 15] C.[3; 0; 15] D.[15; 0; 3]
4.12. Маятник, состоящий из невесомой нити длиной 1 м и свинцового шарика радиусом 0,02 м, совершает гармонические колебания с амплитудой 0,06 м. Определите: а) модуль максимального значения возвращающей силы; б) модуль максимальной скорости. Плотность свинца 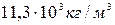 .
.
A.[0,22 Н; 0,18 м/с] B.[0,11 Н; 0,09 м/с]
С.[0,18 Н; 0,22 м/с] D.[0,09 Н; 0,11 м/с]
4.13. Тонкий обруч радиусом 0,5 м подвешен на вбитый в стенку гвоздь и совершает гармонические колебания в плоскости, параллельной стене. Определите частоту колебаний обруча.
A.[0,5 Гц] B.[1 Гц] C.[1,5 Гц] D.[2 Гц]
4.14. Диск радиусом R подвешен так, что может совершать гармонические колебания относительно образующей диска. Определите период и частоту колебаний диска.
A.[ 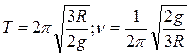 ] B.[
] B.[ 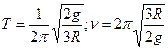 ]
]
C.[ 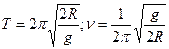 ] D.[
] D.[ 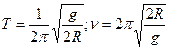 ]
]
4.15. Определите амплитуду и начальную фазу гармонического колебания, полученного от сложения одинаково направленных колебаний, заданных уравнениями:  и
и 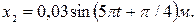
A.[А=0,046 м; 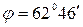 ] В.[А=0,023 м;
] В.[А=0,023 м; 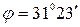 ]
]
С.[А=0,015 м; 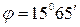 ] С.[А=0,007 м;
] С.[А=0,007 м; 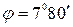 ]
]
4.16. Найти уравнение результирующего колебания, полученного от сложения одинаково направленных колебаний, заданных уравнениями: 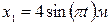 и
и 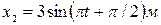 .
.
A.[ 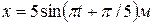 ] B.[
] B.[ 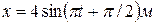 ]
]
C.[ 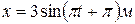 ] D.[
] D.[ 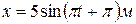 ]
]
4.17. Записать уравнение результирующего колебания точки, полученного от сложения двух взаимно перпендикулярных колебаний одинаковой частоты 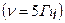 , с одинаковыми начальными фазами, равными
, с одинаковыми начальными фазами, равными 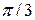 и с амплитудами:
и с амплитудами: 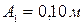 и
и 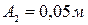 .
.
A.[ 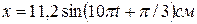 ] В.[
] В.[ 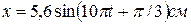 ]
]
C.[ 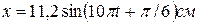 ] D.[
] D.[ 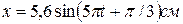 ]
]
4.18. Точка участвует одновременно в двух колебаниях одного направления, которые происходят по законам: 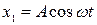 и
и 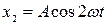 . Найти максимальную скорость точки.
. Найти максимальную скорость точки.
A.[2,73 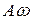 ] B.[273
] B.[273 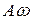 ] C.[2,73
] C.[2,73 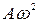 ] D.[273
] D.[273 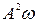 ]
]
4.19. Уравнение затухающих колебаний точки дано в виде 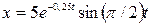 м. Определите скорость точки в моменты времени, равные 0, Т, 2 Т.
м. Определите скорость точки в моменты времени, равные 0, Т, 2 Т.
A.[7,8 м/с; 2,9 м/с; 1,1 м/с] В.[17,6 м/с; 5,8 м/с; 2,2 м/с]
С.[3,9 м/с; 1,4 м/с; 0,5 м/с] D.[2,1 м/с; 0,7 м/с; 0,25 м/с]
4.20. Логарифмический декремент затухания математического маятника равен 0,2. Во сколько раз уменьшится амплитуда за одно полное колебание?
A.[1,22] B.[0,61] C.[0,3] D.[0,2]
4.21*. Маятник представляет собой тонкий однородный стержень длиной 0,5 м. Определите, на каком расстоянии от центра стержня должна быть точка подвеса, чтобы частота колебаний была максимальной. [ 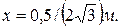 ]
]
4.22*. Математический маятник длиной 1 м подвешен к потолку кабины лифта, которая начинает опускаться вниз с ускорением 2,5 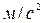 . Спустя время 3 с после начала движения лифт движется равномерно, а затем в течение 3 с с торможением до полной остановки. Определите периоды колебаний маятника на каждом участке пути. [2,3 с; 2,0 с; 1,8 с]
. Спустя время 3 с после начала движения лифт движется равномерно, а затем в течение 3 с с торможением до полной остановки. Определите периоды колебаний маятника на каждом участке пути. [2,3 с; 2,0 с; 1,8 с]
4.23*. Точка участвует в двух колебаниях одинаковой частоты и с одинаковыми начальными фазами. Амплитуды колебаний соответственно равны 3 см и 4 см. Определите амплитуду результирующего колебания, если колебания совершаются: а) в одном направлении; б) в двух взаимноперпендикулярных направлениях. [7 см; 5 см]
4.24*. Однородный диск радиусом 20 см колеблется около горизонтальной оси, проходящей на расстоянии 15 см от центра диска. Определите период колебаний диска. [1,07 c]
4.25*. Начальная амплитуда затухающих колебаний точки равна 3 см. По истечении 10 с от начала колебаний амплитуда стала равной 1 см. Через какое время амплитуда станет равной 0,3 см? [21 c]
4.26*. На горизонтально расположенной пружине жёсткостью 900 Н/м закреплён шар массой 4 кг, лежащий на столе, по которому он может скользить без трения. Пуля массой 10 г, летящая горизонтально со скоростью 600 м/с и имеющая в момент удара скорость, направленную вдоль оси пружины, попала в шар и застряла в нём. Пренебрегая массой пружины и сопротивлением воздуха, определите: а) амплитуду колебания шара; б) период колебаний шара. [0,1 м; 0,42 с]
4.27*. Определите период колебаний тела внутри тоннеля, прорытого через центр Земли, принимая её за однородный шар радиусом 6400 км. Средняя плотность Земли 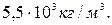 [83,3 мин]
[83,3 мин]
4.28*. На какую высоту надо поднять математический маятник, чтобы период его колебаний увеличился в 2 раза? Радиус Земли 6400 км. [ 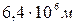 ]
]
4.29*. Найти период вертикальных колебаний шарика массой 40 г, укреплённого на середине горизонтально натянутой струны длиной 1 м. Натяжение струны считать постоянным и равным 10 Н. [0,2 с]
4.30*. Определите период колебаний математического маятника, длина нити которого 20 см, если он находится в однородной жидкости, плотность которой в 3 раза меньше плотности шарика. [1,1 с]






