ФИЗИКА
Задания для тестового контроля аудиторной и самостоятельной работы студентов на практических занятиях по курсу общей физики
Часть 1
Механика и молекулярная физика
Учебно-методическое пособие
Ростов-на-Дону
Составители: С.И. Егорова
В.С. Ковалева
В.С. Кунаков
Г.Ф. Лемешко
Ю.М. Наследников
УДК 530.1
Ф.48 Физика: Задания для тестового контроля аудиторной и самостоятельной работы студентов на практических занятиях по курсу общей физики. Часть 1. Механика и молекулярная физика: Учебно-методическое пособие. – Ростов н/Д: Издательский центр ДГТУ, 2004 - 49 с.
Цель пособия – обеспечить личностно-ориентированный подход к практическим занятиям по общей физике, учитывающий степень подготовки студентов и количество аудиторных часов, выделяемых на лекционные и практические занятия по курсу общей физики по потокам и группам. Пособие предназначено для обучения и контроля работы студентов на практических занятиях по разделу «Механика и молекулярная физика» в течение первого семестра обучения.
Печатается по решению редакционно-издательского совета Донского государственного технического университета
Научный редактор: д.т.н. проф. В.С. Кунаков
Рецензент: д.т.н. проф. Ю.М. Вернигоров
© Издательский центр ДГТУ, 2004
Общие методические указания
Структура практических занятий по курсу физики реализуется в виде трех семестров обучения, каждый из которых разбит на три блока рейтингового контроля знаний. С целью обеспечения дифференцированного подхода и объективности контроля аудиторной и самостоятельной работы студентов на практических занятиях по механике и молекулярной физике подобраны задачи в рамках тестовых заданий.
Они содержат задачи с выбором ответа и задачи с развернутым ответом, отмеченные звездочкой.
При оформлении задач с развернутым ответом необходимо соблюдать следующие требования:
1. Записать краткое условие задачи, выразить все известные величины в одной и той же системе единиц (как правило, в СИ). При необходимости ввести дополнительные постоянные физические величины, приведенные в справочных таблицах «Приложения».
2. Решение задач следует сопровождать краткими, но исчерпывающими объяснениями. При необходимости дать чертеж или график, выполненные с помощью чертежных принадлежностей.
3. Решать задачу надо в общем виде, выразив искомую величину в буквенных обозначениях, заданных в условии задачи.
4. Произвести вычисления.
При оформлении заданий с выбором ответа необходимо привести номер задачи с указанием подраздела курса (напр., 1.25) и выбранный ответ в буквенном или числовом виде. Необходимо дать краткое без пояснений решение задачи, что позволяет выяснить ход рассуждений студента, степень ошибки или правильного ответа.
В «Приложении» даются варианты контрольных заданий.
В течение семестра студенты выполняют две контрольные работы: первую по механике и вторую по молекулярной физике.
В случае неудовлетворительной оценки по контрольной работе студент самостоятельно исправляет ошибки и сдает контрольную работу на повторную проверку. Результаты тестового контроля аудиторной и самостоятельной работы студентов на практических занятиях учитываются лектором при приеме экзаменов и дифференцированных зачетов.
Элементы кинематики
Основные формулы и законы
· Средняя и мгновенная скорости материальной точки


где  - перемещение точки за время D t,
- перемещение точки за время D t,  - радиус-вектор точки.
- радиус-вектор точки.
· Для прямолинейного равномерного движения
 ,
,
где S – путь, пройденный точкой за время D t.
· Среднее и мгновенное ускорения материальной точки


· Полное ускорение при криволинейном движении


где  - тангенциальная составляющая ускорения;
- тангенциальная составляющая ускорения;  - нормальная составляющая ускорения (R -радиус кривизны траектории в данной точке).
- нормальная составляющая ускорения (R -радиус кривизны траектории в данной точке).
· Путь и скорость для равнопеременного движения материальной точки

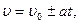
где  - начальная скорость.
- начальная скорость.
· Угловая скорость

· Угловое ускорение

· Угловая скорость для равномерного вращательного движения твердого тела

где T – период вращения;  - частота вращения (N – число оборотов, совершаемых телом за время t).
- частота вращения (N – число оборотов, совершаемых телом за время t).
· Угол поворота и угловая скорость для равнопеременного вращательного движения твердого тела
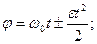

где  - начальная угловая скорость.
- начальная угловая скорость.
· Связь между линейными и угловыми величинами:
 ;
;  ;
;  ;
; 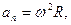
где R – расстояние точки от оси вращения.
1.1. Пароход идет по реке от пункта А до пункта В со скоростью 10 км/ч, а обратно - со скоростью 16 км/ч. Найти: 1) среднюю скорость парохода, 2) скорость течения реки.
А. [12,3 км/ч, 0,83 м/с] В. [12,3 м/с, 0,83 м/с]
С. [12,3 км/ч, 0,83 км/с] D. [13 км/ч, 1,67 м/с]
1.2. Скорость течения реки 3 км/ч, а скорость движения лодки относительно воды 6 км/ч. Определите, под каким углом относительно берега должна двигаться лодка, чтобы проплыть поперек реки.
А. [60°] В. [45°]
С. [30°] D. [90°]
1.3. Велосипедист проехал первую половину времени своего движения со скоростью 16 км/ч, вторую половину времени — со скоростью 12 км/ч. Определите среднюю скорость движения велосипедиста.
А. [14 км/ч] В. [28 км/ч]
С. [4 км/ч] D. [2 км/ч]
1.4. Велосипедист проехал первую половину пути со скоростью 16 км/ч, вторую половину пути — со скоростью 12 км/ч. Определите среднюю скорость движения велосипедиста.
А. [13,7 км/ч]. В. [14 км/ч]
С. [4 км/ч] D. [7 км/ч]
1.5. Студент проехал половину пути на велосипеде со скоростью 16 км/ч. Далее в течение половины оставшегося времени он ехал со скоростью 12 км/ч, а затем до конца пути шел пешком со скоростью 5 км/ч. Определите среднюю скорость движения студента на всем пути.
А. [11,1 км/ч] Б. [11,0 км/ч]
С. [16,5 км/ч] D. [11,1 м/с]
1.6. После удара клюшкой шайба скользит по льду с постоянным ускорением. В конце пятой секунды после начала движения ее скорость была равна 1,5 м/с, а в конце шестой секунды шайба остановилась. С каким ускорением двигалась шайба, какой путь прошла и какова была ее скорость на расстоянии 20 м от начала движения?
А. [1,5 м/c2, 27 м, 4,6 м/с] В. [1,5 м/c2, 10 м, 4,6 км/с]
С. [0,5 м/c2, 27 км, 4,6 м/с] D. [1,5 м/c2, 17 м, 4,6 км/с]
1.7. Тело, брошенное вертикально вверх, через 3с после начала движения имело скорость 7 м/с. На какую максимальную высоту относительно места броска поднималось тело? Сопротивлением воздуха пренебречь.
А. [67,6 м] В. [67,6 км]
С. [97,6 м] D. [97,6 км]
1.8. С башни в горизонтальном направлении брошено тело с начальной скоростью 10 м/с. Пренебрегая сопротивлением воздуха, определите для момента времени  = 2 с после начала движения: 1) скорость тела; 2) радиус кривизны траектории.
= 2 с после начала движения: 1) скорость тела; 2) радиус кривизны траектории.
А. [22 м/с, 109 м] В. [22 м/с, 109 км]
С. [22 км/с, 109 м] D. [22 км/с, 109 км]
1.9. Камень брошен горизонтально со скоростью 5м/с. Определите нормальное и тангенциальное ускорения камня через 1 с после начала движения. Сопротивлением воздуха пренебречь.
А. [4,45 м/с2, 8,73 м/с2] В. [4,45 м/с2, 8,73 км/с2]
С. [4,45 км/с2, 8,73 м/с2] D. [4,45 км/с2, 8,73 км/с2]
1.10. Тело падает вертикально с высоты 19,6 м с нулевой начальной скоростью. Какой путь пройдет тело: 1) за первую 0,1 с своего движения, 2) за последнюю 0,1 с своего движения? Сопротивлением воздуха пренебречь.
А. [0,049 м, 1,9 м] В. [0,049 м, 1,9 км]
С. [0,049 км, 1,9 м] D. [0,049 км, 1,9 км]
1.11. Тело падает вертикально с высоты 19,6 м с нулевой начальной скоростью. За какое время тело пройдет: 1) первый 1 м своего пути, 2) последний 1 м своего пути? Сопротивлением воздуха пренебречь.
А. [0,45 с, 0,05 с] В. [0,045 с, 0,005 с]
С. [4,5 с, 0,5 с] D. [19,6 с, 1 с]
1.12. Два автомобиля, выехав одновременно из одного пункта, движутся прямолинейно в одном направлении. Зависимость пройденного ими пути задается уравнениями  и
и  . Определите закон изменения относительной скорости автомобилей.
. Определите закон изменения относительной скорости автомобилей.
А. [  ] В. [
] В. [  ]
]
С. [ 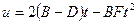 ] D. [
] D. [  ]
]
1.13. Кинематические уравнения движения двух материальных точек имеют вид  и
и  , где
, где  ,
,  = -2 м/с2,
= -2 м/с2,  = 1 м/с2. Определите: 1) момент времени, для которого скорости этих точек будут равны; 2) ускорения а 1 и а 2 для этого момента.
= 1 м/с2. Определите: 1) момент времени, для которого скорости этих точек будут равны; 2) ускорения а 1 и а 2 для этого момента.
А. [1) 0; 2)  = -4 м/с2,
= -4 м/с2, 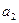 = 2 м/с2] В. [1)1 с; 2)
= 2 м/с2] В. [1)1 с; 2)  = 4 м/с2,
= 4 м/с2, 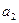 =- 2 м/с2]
=- 2 м/с2]
С. [1) 2 с; 2)  = -4 м/с2,
= -4 м/с2, 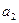 = 2 м/с2] D. [1) 0; 2)
= 2 м/с2] D. [1) 0; 2)  = 4 м/с2,
= 4 м/с2, 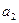 = 2 м/с2]
= 2 м/с2]
1.14. Диск радиусом 5 см вращается вокруг неподвижной оси так, что зависимость угловой скорости от времени задается уравнением  (
(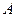 = 2 рад/с2,
= 2 рад/с2, 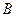 = 1 рад/с5). Определите для точек на ободе диска к концу первой секунды после начала движения: 1) полное ускорение; 2) число оборотов, сделанных диском.
= 1 рад/с5). Определите для точек на ободе диска к концу первой секунды после начала движения: 1) полное ускорение; 2) число оборотов, сделанных диском.
А. [4,22 м/c2; 0, 477] В. [2 м/c2; 1]
С. [1 м/c2; 0, 477] D. [2 м/c2; 2]
1.15. Нормальное ускорение точки, движущейся по окружности радиусом  = 4 м, задается уравнением
= 4 м, задается уравнением 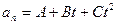 (
(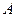 = 1 м/с2,
= 1 м/с2, 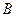 = 6 м/с3,
= 6 м/с3,  = 9 м/с4). Определите: 1) тангенциальное ускорение точки; 2) путь, пройденный точкой за время
= 9 м/с4). Определите: 1) тангенциальное ускорение точки; 2) путь, пройденный точкой за время  = 5 с после начала движения; 3) полное ускорение для момента времени
= 5 с после начала движения; 3) полное ускорение для момента времени 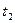 = 1 с.
= 1 с.
А. [1) 6 м/с2; 2) 85 м; 3) 17,1 м/с2] В. [1) 1 м/с2; 2) 6 м; 3) 9 м/с2]
С. [1) 6 км/с2; 2) 85 км; 3) 17,1 м/с2] D. [1) 6 м/с2; 2) 85 м; 3) 17,1 км/с2]
1.16. Зависимость пройденного телом пути  от времени
от времени  выражается уравнением
выражается уравнением  (
(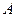 = 2 м/с,
= 2 м/с, 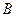 = 3 м/с2,
= 3 м/с2,  = 4 м/с3). Запишите выражения для скорости и ускорения. Определите для момента времени
= 4 м/с3). Запишите выражения для скорости и ускорения. Определите для момента времени  = 2 с после начала движения: 1) пройденный путь; 2) скорость; 3) ускорение.
= 2 с после начала движения: 1) пройденный путь; 2) скорость; 3) ускорение.
А. [1) 24 м; 2) 38 м/с; 3) 42 м/с2] В. [1) 2 м; 2) 3 м/с; 3) 4 м/с2]
С. [1) 24 км; 2) 11 км/с; 3) 4 км/с2] D. [1) 5 м; 2) 38 км/с; 3) 42 м/с2]
1.17. Зависимость пройденного телом пути по окружности радиусом  = 3 м задается уравнением
= 3 м задается уравнением  (
(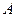 = 0,4 м/с2,
= 0,4 м/с2, 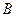 = 0,1 м/с). Для момента времени
= 0,1 м/с). Для момента времени  = 1 с после начала движения определите ускорения: 1) нормальное; 2) тангенциальное; 3) полное.
= 1 с после начала движения определите ускорения: 1) нормальное; 2) тангенциальное; 3) полное.
A. [1) 0,27 м/с2; 2) 0,8 м/с2; 3) 0,84 м/с2]
B. [1) 0,27 км/с2; 2) 0,8 км/с2; 3) 0,84 км/с2]
C. [1) 2,7 м/с2; 2) 8 м/с2; 3) 8,4 м/с2]
D. [1) 0,027 м/с2; 2) 0,08 м/с2; 3) 0,084 м/с2]
1.18. Радиус-вектор материальной точки изменяется со временем по закону 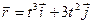 , где
, где  - орты осей
- орты осей  и
и  . Определите для момента времени
. Определите для момента времени  = 1 с: 1) модуль скорости; 2) модуль ускорения.
= 1 с: 1) модуль скорости; 2) модуль ускорения.
А. [1) 6,7 м/с; 2) 8,48 м/с2] В. [1) 6,7к м/с; 2) 8,48 км/с2]
С. [1) 3 м/с; 2) 6 м/с2] D. [1) 6 м/с; 2) 3 м/с2]
1.19. Радиус-вектор материальной точки изменяется со временем по закону 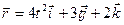 . Определите: 1) скорость
. Определите: 1) скорость  ; 2) ускорение
; 2) ускорение  ; 3) модуль скорости в момент времени
; 3) модуль скорости в момент времени  = 2 с.
= 2 с.
А. [3) 16,3 м/с] В. [3) 8 м/с]
С. [3) 9 м/с] D. [3) 16,3 км/с]
1.20. Движение материальной точки в плоскости  ,
,  описывается законом
описывается законом  ,
,  , где
, где 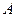 и
и 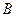 - положительные постоянные. Определите: 1) уравнение траектории материальной точки
- положительные постоянные. Определите: 1) уравнение траектории материальной точки  ; 2) радиус-вектор
; 2) радиус-вектор  точки в зависимости от времени; 3) скорость точки в зависимости от времени; 4) ускорение точки в зависимости от времени.
точки в зависимости от времени; 3) скорость точки в зависимости от времени; 4) ускорение точки в зависимости от времени.
А.[1)  2)
2) 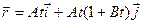 ;3)
;3)  ;4)
;4)  ]
]
В.[1)  2)
2) 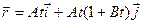 ; 3)
; 3)  ;4)
;4)  ]
]
С.[1)  2)
2)  ; 3)
; 3)  ;4)
;4)  ]
]
D.[1)  2)
2) 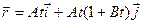 ; 3)
; 3) 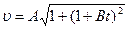 ;4)
;4)  ]
]
1.21. Материальная точка начинает двигаться по окружности радиусом  = 2,5 см с постоянным тангенциальным ускорением
= 2,5 см с постоянным тангенциальным ускорением  = 0,5 см/с2. Определите: 1) момент времени, при котором вектор ускорения
= 0,5 см/с2. Определите: 1) момент времени, при котором вектор ускорения  образует с вектором скорости
образует с вектором скорости  угол 45°; 2) путь, пройденный за это время движущейся точкой.
угол 45°; 2) путь, пройденный за это время движущейся точкой.
А. [1) 5 с; 2) 6,25 см] В. [1) 0,5 с; 2) 62,5 см]
С. [1) 2,5 с; 2) 62,5 см] D. [1) 0,5 с; 2) 62,5 см]
1.22. Линейная скорость точки, находящейся на ободе вращающегося диска, в три раза больше, чем линейная скорость точки, находящейся на 6 см ближе к его оси. Определите радиус диска.
А. [9 см] В. [6 см]
С. [9 м] D. [6 м]
1.23. Колесо вращается с постоянным угловым ускорением 3 рад/с2. Определите радиус колеса, если через 1 с после начала движения полное ускорение колеса 7,5 м/с2.
А. [79 см] В. [9 м]
С. [9 см] D. [79 м]
1.24. Якорь электродвигателя, имеющий частоту вращения 50 с-1, после выключения тока, сделав 628 оборотов, остановился. Определите угловое ускорение якоря.
А. [12,5 рад/с2] В. [628 рад/с2]
С. [25 рад/с2] D. [50 рад/с2]
1.25. Колесо автомобиля вращается равнозамедленно. За время 2 мин оно изменило частоту вращения от 240 до 60 мин-1. Определите: 1) угловое ускорение колеса; 2) число полных оборотов, сделанных колесом за это время.
А. [1) 0,157 рад/с2; 2) 300] В. [1) 0,157 рад/с2; 2) 240]
С. [1) 1,57 рад/с2; 2) 300] D. [1) 1,57 рад/с2; 2) 240]
1.26. Диск радиусом 10 см вращается вокруг неподвижной оси так, что зависимость угла поворота радиуса диска от времени задается уравнением  (
(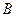 = 1 рад/с2,
= 1 рад/с2,  = 1 рад/с2,
= 1 рад/с2, 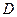 = 1 рад/с3). Определите для точек на ободе диска к концу второй секунды после начала движения: 1) тангенциальное ускорение; 2) нормальное ускорение; 3) полное ускорение.
= 1 рад/с3). Определите для точек на ободе диска к концу второй секунды после начала движения: 1) тангенциальное ускорение; 2) нормальное ускорение; 3) полное ускорение.
А. [1) 1,4 м/с2; 2) 28,9 м/с2; 3) 28,9 м/с2]
В. [1) 1,4 км/с2; 2) 28,9 км/с2; 3) 28,9 км/с2]
С. [1) 1 км/с2; 2) 2,8 км/с2; 3) 2,8 км/с2]
D. [1) 1 м/с2; 2) 2,8 м/с2; 3) 2,8 м/с2]
1.27. Диск вращается вокруг неподвижной оси так, что зависимость угла поворота радиуса диска от времени задается уравнением 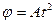 (
(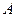 = 0,5 рад/с2). Определите к концу второй секунды после начала движения: 1) угловую скорость диска; 2) угловое ускорение диска; 3) для точки, находящейся на расстоянии 80 см от оси вращения, тангенциальное, нормальное и полное ускорения.
= 0,5 рад/с2). Определите к концу второй секунды после начала движения: 1) угловую скорость диска; 2) угловое ускорение диска; 3) для точки, находящейся на расстоянии 80 см от оси вращения, тангенциальное, нормальное и полное ускорения.
А. [1) 2 рад/с; 2) 1 рад/с2; 3)  = 0,8 м/с2,
= 0,8 м/с2,  = 3,2 м/с2, а = 3,3 м/с2]
= 3,2 м/с2, а = 3,3 м/с2]
В. [1) 2 рад/с; 2) 2 рад/с2; 3)  = 8 км/с2,
= 8 км/с2,  = 3,2 км/с2, а = 3,3 км/с2]
= 3,2 км/с2, а = 3,3 км/с2]
С. [1) 1 рад/с; 2) 2 рад/с2; 3)  = 0,8 м/с2,
= 0,8 м/с2,  = 3,2 м/с2, а = 3,3 м/с2]
= 3,2 м/с2, а = 3,3 м/с2]
D. [1) 1 рад/с; 2) 2 рад/с2; 3)  = 0,8 км/с2,
= 0,8 км/с2,  = 3,2 км/с2, а = 3,3 км/с2]
= 3,2 км/с2, а = 3,3 км/с2]
1.28. Диск вращается вокруг неподвижной оси так, что зависимость угла поворота радиуса диска от времени задается уравнением 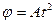 (
(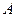 = 0,1 рад/с2). Определите полное ускорение точки на ободе диска к концу второй секунды после начала движения, если в этот момент линейная скорость этой точки 0,4 м/с.
= 0,1 рад/с2). Определите полное ускорение точки на ободе диска к концу второй секунды после начала движения, если в этот момент линейная скорость этой точки 0,4 м/с.
А. [0,25 м/с2] В. [0,25 км/с2]
С. [0,1 м/с2] D. [0,1 км/с2]
1.29. Диск радиусом 10 см вращается так, что зависимость линейной скорости точек, лежащих на ободе диска, от времени задается уравнением 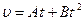 (
(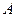 = 0,3 м/с2,
= 0,3 м/с2, 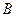 = 0,1 м/с3). Определите момент времени, для которого вектор полного ускорения образует с радиусом колеса угол
= 0,1 м/с3). Определите момент времени, для которого вектор полного ускорения образует с радиусом колеса угол  = 4°.
= 4°.
А. [2 с] В. [0,3 с] С. [0,1 с] D. [0,2 с]
1.30. Диск радиусом 10 см вращается так, что зависимость угла поворота радиуса диска от времени задается уравнением  (
(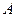 = 2 рад,
= 2 рад, 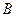 = 4 рад/с3). Определите для точек на ободе колеса: 1) нормальное ускорение в момент времени 2 с; 2) тангенциальное ускорение для этого же момента; 3) угол поворота, при котором полное ускорение составляет с радиусом колеса 45°.
= 4 рад/с3). Определите для точек на ободе колеса: 1) нормальное ускорение в момент времени 2 с; 2) тангенциальное ускорение для этого же момента; 3) угол поворота, при котором полное ускорение составляет с радиусом колеса 45°.
А. [1) 230 м/с2; 2) 4,8 м/с2; 3) 2,67 рад]
В. [1) 230 км/с2; 2) 4,8 км/с2; 3) 26,7 рад]
С. [1) 23 м/с2; 2) 0,48 м/с2; 3) 2,67 рад]
D. [1) 2,3 м/с2; 2) 48 м/с2; 3) 26,7 рад]
1.31.* За промежуток времени t = 10 с точка прошла половину окружности радиуса R = 160 см. Вычислить за это время: 1) среднее значение модуля скорости; 2) модуль среднего вектора скорости; 3) модуль среднего вектора полного ускорения, если точка двигалась с постоянным тангенциальным ускорением. [1)  2)
2)  3)
3) 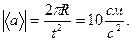 ]
]
1.32.* Точка движется по дуге окружности радиуса R. Ее скорость зависит от пройденного пути S по закону 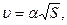 где
где 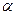 - постоянная. Найти зависимость угла
- постоянная. Найти зависимость угла  между вектором полного ускорения и вектором скорости от пути S. [
между вектором полного ускорения и вектором скорости от пути S. [  ]
]
1.33.* Точка движется по плоскости так, что ее тангенциальное ускорение 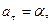 а нормальное ускорение
а нормальное ускорение 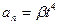 , где
, где 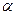 и
и  - положительные постоянные, t – время. В момент времени t = 0 точка покоилась. Найти зависимость от пройденного пути S радиуса кривизны R траектории точки и ее полного ускорения a. [
- положительные постоянные, t – время. В момент времени t = 0 точка покоилась. Найти зависимость от пройденного пути S радиуса кривизны R траектории точки и ее полного ускорения a. [ 
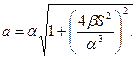 ]
]
Динамика материальной точки и поступательного движения твердого тела
Основные законы и формулы
· Импульс материальной точки
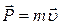 .
.
· Второй закон Ньютона (основное уравнение динамики материальной точки)

· Это же уравнение в проекциях на касательную и нормаль к траектории точки


· Сила трения скольжения

где m — коэффициент трения скольжения; N — сила нормального давления.
· Закон сохранения импульса для замкнутой системы

где n - число материальных точек (или тел), входящих в систему.
· Координаты центра масс системы материальных точек:

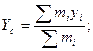

где 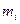 — масса
— масса  -й материальной точки;
-й материальной точки;  - ее координаты.
- ее координаты.
· Работа, совершаемая телом
 ,
,
где  — проекция силы на направление перемещения;
— проекция силы на направление перемещения; 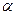 — угол между направлениями силы и перемещения.
— угол между направлениями силы и перемещения.
· Работа, совершаемая переменной силой, на пути s
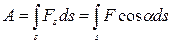
· Средняя мощность за промежуток времени 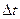
 ,
,
где D А – работа за промежуток времени D t.
· Мгновенная мощность
 , или
, или  .
.
· Кинетическая энергия движущегося со скоростью u тела массой m
 .
.
· Связь между силой, действующей на тело в данной точке поля, и потенциальной энергией тела
 , или
, или  ,
,
где  - единичные векторы координатных осей.
- единичные векторы координатных осей.
· Потенциальная энергия тела массой m, поднятого над поверхностью земли на высоту h,
 ,
,
где 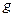 - ускорение свободного падения.
- ускорение свободного падения.
· Сила упругости
 ,
,
где  - величина деформации;
- величина деформации;  - коэффициент жесткости.
- коэффициент жесткости.
· Потенциальная энергия упругодеформированного тела

· Закон сохранения механической энергии (для консервативной системы)

· Механическое напряжение при упругой деформации тела

где  - растягивающая (сжимающая) сила;
- растягивающая (сжимающая) сила;  - площадь поперечного сечения тела.
- площадь поперечного сечения тела.
· Закон Гука для продольного растяжения (сжатия)

где  - модуль упругости (модуль Юнга), e - относительное удлинение (сжатие).
- модуль упругости (модуль Юнга), e - относительное удлинение (сжатие).
· Сила гравитационного притяжения двух материальных точек
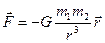 ,
,
где G – гравитационная постоянная, m 1 и m 2 – массы взаимодействующих точек,  - радиус-вектор, проведенный из центра масс системы к материальной точке.
- радиус-вектор, проведенный из центра масс системы к материальной точке.
· Потенциальная энергия гравитационного взаимодействия
 .
.
2.1. Через блок, укрепленный на конце стола, перекинута нерастяжимая нить, к концам которой прикреплены грузы, один из которых ( = 400 г) движется по поверхности стола, а другой (
= 400 г) движется по поверхности стола, а другой ( = 600 г) — вдоль вертикали вниз. Коэффициент трения груза о стол равен 0,1. Считая нить и блок невесомыми, определите: 1) ускорение
= 600 г) — вдоль вертикали вниз. Коэффициент трения груза о стол равен 0,1. Считая нить и блок невесомыми, определите: 1) ускорение  , с которым движутся грузы; 2) силу натяжения
, с которым движутся грузы; 2) силу натяжения  нити.
нити.
А. [1)  = 5,49 м/с2; 2)
= 5,49 м/с2; 2)  = 2,59 Н] В. [1)
= 2,59 Н] В. [1)  = 5,49 км/с2; 2)
= 5,49 км/с2; 2)  = 2,59 кН]
= 2,59 кН]
С. [1)  = 5,49 м/с2; 2)
= 5,49 м/с2; 2)  = 2,59 кН] D. [1)
= 2,59 кН] D. [1)  = 5,49 км/с2; 2)
= 5,49 км/с2; 2)  = 2,59 Н]
= 2,59 Н]
 2.2. Два груза (
2.2. Два груза ( = 500 г и
= 500 г и  = 700 г) связаны невесомой нитью и лежат на гладкой горизонтальной поверхности (рис. 1). К грузу
= 700 г) связаны невесомой нитью и лежат на гладкой горизонтальной поверхности (рис. 1). К грузу  приложена горизонтально направленная сила
приложена горизонтально направленная сила  = 6 Н. Пренебрегая трением, определите: 1) ускорение грузов; 2) силу натяжения нити
= 6 Н. Пренебрегая трением, определите: 1) ускорение грузов; 2) силу натяжения нити
А. [1) 5 м/с2; 2) 3,5 Н] В. [1) 5 км/с2; 2) 3,5 кН]
С. [1) 0,5 м/с2; 2) 0,35 Н] D. [1) 0,5 км/с2; 2) 0,35 кН]
 2.3. Простейшая машина Атвуда, применяемая для изучения законов равноускоренного движения, представляет собой два груза с неравными массами
2.3. Простейшая машина Атвуда, применяемая для изучения законов равноускоренного движения, представляет собой два груза с неравными массами  и
и  , которые подвешены на легкой нити, перекинутой через неподвижный блок (рис. 2). Считая нить и блок невесомыми, пренебрегая трением в оси блока и полагая
, которые подвешены на легкой нити, перекинутой через неподвижный блок (рис. 2). Считая нить и блок невесомыми, пренебрегая трением в оси блока и полагая  >
>  , определите: 1) ускорение
, определите: 1) ускорение  грузов; 2) силу натяжения нити
грузов; 2) силу натяжения нити  ; 3) силу
; 3) силу  , действующую на ось блока.
, действующую на ось блока.
А. [1)  ; 2)
; 2)  ; 3)
; 3)  ]
]
В. [1) 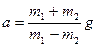 ; 2)
; 2)  ; 3)
; 3)  ]
]
С. [1)  ; 2)
; 2)  ; 3)
; 3)  ]
]
D. [1)  ; 2)
; 2)  ; 3)
; 3) 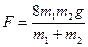 ]
]
2.4. Тело массой 2 кг движется прямолинейно по закону  (
( = 2 м/с2,
= 2 м/с2, 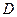 = 0,4 м/с3). Определите силу, действующую на тело в конце первой секунды движения.
= 0,4 м/с3). Определите силу, действующую на тело в конце первой секунды движения.
А. [3,2 Н] B. [32 Н]
C. [3,2 кН] D. [0,32 Н]
2.5. Тело массой m движется так, что зависимость пройденного пути от времени описывается уравнением 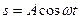 , где
, где 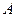 и
и 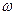 — постоянные. Запишите закон изменения силы от времени.
— постоянные. Запишите закон изменения силы от времени.
A. [  ] B. [
] B. [ 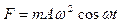 ]
]
C. [  ] D. [
] D. [  ]
]
2.6. К нити подвешен груз массой 500 г. Определите силу натяжения нити, если нить с грузом: 1) поднимать с ускорением 2 м/с2; 2) опускать с ускорением 2м/с2.
A. [1) 5,9 Н, 2) 3,9 Н] B. [1) 5,9 кН, 2) 3,9 Н]
C. [1) 5,9 кН, 2) 3,9 кН] D. [1) 5,9 Н, 2) 3,9 кН]
 2.7. На (рис. 3) изображена система блоков, к которым подвешены грузы массами
2.7. На (рис. 3) изображена система блоков, к которым подвешены грузы массами  = 200 г и
= 200 г и  = 500 г. Считая, что груз
= 500 г. Считая, что груз  поднимается, а подвижный блок с грузом
поднимается, а подвижный блок с грузом  опускается, нить и блоки невесомы, силы трения отсутствуют, определите: 1) силу натяжения нити
опускается, нить и блоки невесомы, силы трения отсутствуют, определите: 1) силу натяжения нити  ; 2) ускорения, с которыми движутся грузы.
; 2) ускорения, с которыми движутся грузы.
A. [1)  = 2,26 Н; 2)
= 2,26 Н; 2)  = 1,5 м/с2, 3)
= 1,5 м/с2, 3) 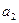 = 0,75 м/с2]
= 0,75 м/с2]
B. [1)  = 2,26 кН; 2)
= 2,26 кН; 2)  = 1,5 м/с2, 3)
= 1,5 м/с2, 3) 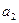 =7,5 м/с2]
=7,5 м/с2]
C. [1)  = 2,26 кН; 2)
= 2,26 кН; 2)  = 15 м/с2, 3)
= 15 м/с2, 3) 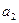 = 0,75 м/с2]
= 0,75 м/с2]
D. [1)  = 2,26 Н; 2)
= 2,26 Н; 2)  = 15 м/с2, 3)
= 15 м/с2, 3) 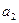 = 7,5 м/с2]
= 7,5 м/с2]
 2.8. В установке (рис. 4) угол
2.8. В установке (рис. 4) угол 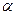 наклонной плоскости с горизонтом равен 20°, массы тел
наклонной плоскости с горизонтом равен 20°, массы тел  = 200 г и
= 200 г и  = 150 г. Считая нить и блок невесомыми и пренебрегая силами трения, определите ускорение, с которым будут двигаться эти тела.
= 150 г. Считая нить и блок невесомыми и пренебрегая силами трения, определите ускорение, с которым будут двигаться эти тела.
A. [2,29 м/с2] B. [23 м/с2]
C. [0,3 м/с2] D. [0,4 м/с2]
2.9 Тело 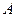 массой 2 кг (рис. 5) находится на горизонтальном столе и соединено нитями посредством блоков с телами
массой 2 кг (рис. 5) находится на горизонтальном столе и соединено нитями посредством блоков с телами 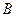 (
( = 0,5 кг) и
= 0,5 кг) и  (
( = 0,3 кг). Считая нити и блоки невесомыми и пренебрегая силами трения, определите: 1) ускорение, с которым будут двигаться эти тела; 2) разность сил натяжения нитей.
= 0,3 кг). Считая нити и блоки невесомыми и пренебрегая силами трения, определите: 1) ускорение, с которым будут двигаться эти тела; 2) разность сил натяжения нитей.
 A. [1) 0,7 м/с2; 2) 1,4 Н]
A. [1) 0,7 м/с2; 2) 1,4 Н]
B. [1) 0,7 м/с2; 2) 1,4 кН]
C. [1) 7 м/с2; 2) 1,4 кН]
D. [1) 7 м/с2; 2) 1,4 Н]
 2.10. В установке (рис. 6) углы
2.10. В установке (рис. 6) углы 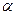 и
и  с горизонтом соответственно равны 30° и 45°, массы тел
с горизонтом соответственно равны 30° и 45°, массы тел  = 0,45 кг и
= 0,45 кг и  = 0,5 кг. Считая нить и блок невесомыми и пренебрегая силами трения, определите: 1) ускорение, с которым движутся тела; 2) силу натяжения нити.
= 0,5 кг. Считая нить и блок невесомыми и пренебрегая силами трения, определите: 1) ускорение, с которым движутся тела; 2) силу натяжения нити.
A. [1) 1,33м/с2; 2) 2,8 Н]
B. [1) 1,33м/с2; 2) 2,8 кН]
C. [1) 13,3м/с2; 2) 2,8 Н]
D. [1) 13,3м/с2; 2) 2,8 кН]
2.11. Тело массой 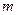 движется в плоскости
движется в плоскости 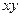 по закону
по закону  ,
, 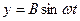 , где
, где  ,
,  и
и 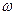 — некоторые постоянные. Определите модуль силы, действующей на это тело.
— некоторые постоянные. Определите модуль силы, действующей на это тело.
A. [ 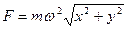 ] B. [
] B. [  ]
]
C. [  ] D. [
] D. [  ]
]
 2.12. На тело (рис. 7) массой 10 кг, лежащее на наклонной плоскости (угол
2.12. На тело (рис. 7) массой 10 кг, лежащее на наклонной плоскости (угол 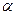 = 20°), действует горизонтально направленная сила
= 20°), действует горизонтально направленная сила  = 8 Н. Пренебрегая трением, определите: 1) ускорение тела; 2) силу, с которой тело давит на плоскость.
= 8 Н. Пренебрегая трением, определите: 1) ускорение тела; 2) силу, с которой тело давит на плоскость.
A. [1) 4,11 м/с2; 2) 89,4 Н]
B. [1) 4,11 м/с2; 2) 89,4 кН]
C. [1) 0,4 м/с2; 2) 89,4 кН] D. [1) 0,4 м/с2; 2) 89,4 Н]
2.13. Тело массой 2 кг падает вертикально с ускорением 5 м/с2. Определите силу сопротивления тела о воздух.
A. [9,62 Н] B. [9,62 кН]
C. [1,0 Н] D. [4,0 Н]
2.14. С вершины клина, длина которого 2 м и высота 1 м, начинает скользить небольшое тело. Коэффициент трения между телом и клином 0,15. Определите: 1) ускорение, с которым движется тело; 2) время прохождения тела вдоль клина; 3) скорость тела у основания клина.
A. [1) 3,63м/с2; 2) 1,05 с; 3) 3,81 м/с] B. [1) 4,63м/с2; 2) 1,05 с; 3) 4,81 м/с]
C. [1) 5,63м/с2; 2) 10,5 с; 3) 5,81 м/с] D. [1) 6,63м/с2; 2) 1,05 с; 3) 6,81 м/с]
2.15. По наклонной плоскости с углом наклона к горизонту, равным 30°, скользит тело. Определите скорость тела в конце второй секунды от начала скольжения, если коэффициент трения 0,15.
A. [7,26 м/с] B. [72,6 м/с]
C. [7,26 км/с] D. [4,26 м/с]
 2.16. Вагон массой 1 т спускается по канатной железной дороге с уклоном
2.16. Вагон массой 1 т спускается по канатной железной дороге с уклоном 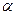 = 15° к горизонту (рис. 8). Принимая коэффициент трения 0,05, определите силу натяжения каната при торможении вагона в конце спуска, если скорость вагона перед торможением 2,5 м/с, а время торможения 6 с.
= 15° к горизонту (рис. 8). Принимая коэффициент трения 0,05, определите силу натяжения каната при торможении вагона в конце спуска, если скорость вагона перед торможением 2,5 м/с, а время торможения 6 с.
A. [2,48 кН] B. [2,48 Н]
C. [248 Н] D. [24,8 Н]
 2.17. Грузы одинаковой массой (
2.17. Грузы одинаковой массой ( =
=  = 0,5 кг) соединены нитью и перекинуты через невесомый блок, укрепленный на конце стола (рис. 9). Коэффициент трения груза
= 0,5 кг) соединены нитью и перекинуты через невесомый блок, укрепленный на конце стола (рис. 9). Коэффициент трения груза  о стол 0,15. Пренебрегая трением в блоке, определите: 1) ускорение, с которым движутся грузы; 2) силу натяжения нити.
о стол 0,15. Пренебрегая трением в блоке, определите: 1) ускорение, с которым движутся грузы; 2) силу натяжения нити.
 A. [1) 4,17 м/с2; 2) 2,82 Н].
A. [1) 4,17 м/с2; 2) 2,82 Н].
B. [1) 4,17 м/с2; 2) 2,82 кН].
C. [1) 41,7 м/с2; 2) 2,82 Н].
D. [1) 41,7 м/с2; 2) 2,82 кН].
2.18. Система грузов (рис. 10) массами  = 0,5 кг и
= 0,5 кг и  = 0,6 кг находится в лифте, движущемся вверх с ускорением
= 0,6 кг находится в лифте, движущемся вверх с ускорением  = 4,9 м/с2. Определите силу натяжения нити
= 4,9 м/с2. Определите силу натяжения нити  , если коэффициент трения между грузом массы
, если коэффициент трения между грузом массы  и опорой 0,1.
и опорой 0,1.
A. [4,41 Н] B. [44,1 Н]
C. [4,41 кН] D. [44,1 кН]
 2.19. В установке (рис. 11) угол
2.19. В установке (рис. 11) угол 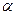 наклона плоскости с горизонтом равен 30°, массы тел одинаковы (
наклона плоскости с горизонтом равен 30°, массы тел одинаковы (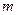 = 1 кг). Считая нить и блок невесомыми и пренебрегая трением в оси блока, определите силу давления
= 1 кг). Считая нить и блок невесомыми и пренебрегая трением в оси блока, определите силу давления  на ось, если коэффициент трения между наклонной плоскостью и лежащим на ней телом 0,1.
на ось, если коэффициент трения между наклонной плоскостью и лежащим на ней телом 0,1.
A. [13,5 Н] B. [1,35 Н]
C. [135 Н] D. [1,35 кН]
 2.20. Определите положение центра масс системы, состоящей из четырех шаров, массы которых равны соответственно
2.20. Определите положение центра масс системы, состоящей из четырех шаров, массы которых равны соответственно 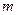 ,
,  ,
,  и
и  , в следующих случаях (рис. 12): а) шары расположены на одной прямой; б) шары расположены по вершинам квадрата; в) шары расположены по четырем смежным вершинам куба. Во всех случаях расстояние между соседними шарами равно 15 см. Направления координатных осей показаны на рисунке.
, в следующих случаях (рис. 12): а) шары расположены на одной прямой; б) шары расположены по вершинам квадрата; в) шары расположены по четырем смежным вершинам куба. Во всех случаях расстояние между соседними шарами равно 15 см. Направления координатных осей показаны на рисунке.
A. [а)  = 30 см; б)
= 30 см; б)  = 7,5 см,
= 7,5 см, 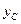 = 4,5 см; в)
= 4,5 см; в)  = 4,5 см,
= 4,5 см, 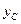 = 1,5 см,
= 1,5 см,  = 3 см]
= 3 см]
B. [а)  = 3 см; б)
= 3 см; б)  = 75 см,
= 75 см, 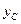 = 4,5 см; в)
= 4,5 см; в)  = 45 см,
= 45 см, 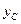 = 1,5 см,
= 1,5 см,  = 3 см]
= 3 см]
C. [а)  = 0,30 см; б)
= 0,30 см; б)  = 0,75 см,
= 0,75 см, 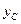 = 4,5 см; в)
= 4,5 см; в)  = 45 см,
= 45 см, 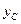 = 15 см,
= 15 см,  = 3 см]
= 3 см]
D. [а)  = 0,03 см; б)
= 0,03 см; б)  = 7,5 см,
= 7,5 см, 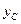 = 0,45 см; в)
= 0,45 см; в)  = 4,5 см,
= 4,5 см, 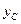 = 15 см,
= 15 см,  = 3 см]
= 3 см]
2.21. Определите координаты центра масс системы, состоящей из четырех шаров массами  ,
,  ,
,  и
и 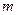 , которые расположены в вершинах и в центре равностороннего треугольника со стороной
, которые расположены в вершинах и в центре равностороннего треугольника со стороной  = 20 см (рис. 13). Направления координатных осей указаны на рисунке.
= 20 см (рис. 13). Направления координатных осей указаны на рисунке.
 A. [
A. [  = 12 см,
= 12 см, 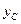 = 5,77 см]
= 5,77 см]
B. [  = 1,2 см,
= 1,2 см, 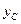 = 5,77 см]
= 5,77 см]
C. [  = 12 см,
= 12 см, 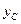 = 57,7 см]
= 57,7 см]
D. [  = 1,2 см,
= 1,2 см, 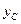 = 57,7 см]
= 57,7 см]
2.23. Груз массой 80 кг поднимают вдоль наклонной плоскости с ускорением 1 м/с2. Длина наклонной плоскости 3 м, угол ее наклона к горизонту равен 30°, а коэффициент трения 0,15. Определите: 1) работу, совершаемую подъемным устройством; 2) его среднюю мощность; 3) его максимальную мощность. Начальная скорость груза равна нулю.
A. [1) 1,72 кДж; 2) 702 Вт; 3) 1,41 кВт]
B. [1) 1,72 Дж; 2) 70,2 Вт; 3) 1,41 Вт]
C. [1) 1,72 Дж; 2) 702 Вт; 3) 1,41 Вт]
D. [1) 1,72 кДж; 2) 70,2 Вт; 3) 1,41 Вт]
2.24. Тело массой 5 кг поднимают с ускорением 2 м/с2. Определите работу силы в течение первых пяти секунд.
A. [1,48 кДж] B. [14,8 кДж]
C. [1,48 Дж] D. [148 Дж]
2.25. Автомобиль массой 1,8 т движется в гору, уклон которой составляет 3 м на каждые 100 м пути. Определите: 1) работу, совершаемую двигателем автомобиля на пути 5 км, если коэффициент трения равен 0,1; 2) развиваемую двигателем мощность, если известно, что этот путь был преодолен за 5 мин.
A. [1) 11,5 МДж; 2) 38,3 кВт] B. [1) 11,5 кДж; 2) 38,3 Вт]
C. [1) 11,5 кДж; 2) 38,3 кВт] D. [1) 11,5 Дж; 2) 38,3 Вт]
2.26. Определите работу, совершаемую при подъеме груза массой 50 кг по наклонной плоскости с углом наклона 30° к горизонту на расстояние 4 м, если время подъема 2 с, а коэффициент трения 0,06.
A. [1,48 кДж] B. [1,48 Дж]
C. [14,8 кДж] D. [148 Дж]
2.27. Тело скользит с наклонной плоскости высотой h и углом наклона 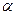 к горизонту и движется далее по горизонтальному участку. Принимая коэффициент трения на всем пути постоянным и равным m, определите расстояние s, пройденное телом на горизонтальном участке, до полной остановки.
к горизонту и движется далее по горизонтальному участку. Принимая коэффициент трения на всем пути постоянным и равным m, определите расстояние s, пройденное телом на горизонтальном участке, до полной остановки.
A. [  ] B. [
] B. [  ]
]
C. [  ] D. [
] D. [ 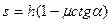 ]
]
2.28. Самолет массой 5 т двигался горизонтально со скоростью 360 км/ч. Затем он поднялся на 2 км. При этом его скорость стала 200 км/ч. Найти работу, затраченную мотором на подъем самолета.
А. [81МДж] В. [81КДж]
С. [-17МДж] D. [173МДж]
2.29. Материальная точка массой 1 кг двигалась под действием некоторой силы согласно уравнению  (
(
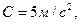
 ). Определите мощность, затрачиваемую на движение точки в момент времени 1 с.
). Определите мощность, затрачиваемую на движение точки в момент времени 1 с.
A. [16 Вт] B. [16 кВт]
C. [16 МВт] D. [1,6 Вт]
2.30. С башни высотой 20 м горизонтально со скоростью 10 м/с брошен камень массой 400 г. Пренебрегая сопротивлением воздуха, определите для момента времени 1 с после начала движения: 1) кинетическую энергию камня; 2) потенциальную энергию.
A. [1) 39,2 Дж; 2) 59,2 Дж] B. [1) 3,92 Дж; 2) 5,92 Дж]
C. [1) 39,2 кДж; 2) 59,2 кДж] D. [1) 39,2 кДж; 2) 592 Дж]
2.31. К нижнему концу пружины жесткостью k 1 присоединена другая пружина жесткостью k 2, к концу которой прикреплена гиря. Пренебрегая массой пружин, определите отношение потенциальных энергий пружин.
A. [П1/П2 = k 2/ k l] B. [П1/П2 = k 2 k l]
C. [П1/П2 = 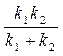 ] D. [П1/П2 = k l+ k 2]
] D. [П1/П2 = k l+ k 2]
2.32. К потолку вагона, движущегося в горизонтальном направлении с ускорением 9,81 м/с2, подвешен на нити шарик массой 200 г. Определите для установившегося движения: 1) силу натяжения нити; 2) угол отклонения нити от вертикали.
A. [1) 2,77 Н; 2) 45°] B. [1) 27,7 Н; 2) 30°]
C. [1) 277 Н; 2) 30°] D. [1) 277 Н; 2) 60°]
2.33. Вагон под действием силы тяжести катится вдоль дороги, составляющей угол 30° с горизонтом. Сила трения составляет 10 % от веса вагона. К потолку вагона на нити подвешен шарик массой 15 г. Определите: 1) силу, действующую на нить; 2) угол отклонения нити от вертикали.
A. [1) 0,128 Н; 2) 23,5°] B. [1) 128 Н; 2) 30,5°]
C. [1) 12,8 Н; 2) 30,5°] D. [1) 1,28 Н; 2) 23,5°]
2.34. Мотоциклист в цирке едет вдоль внутренней поверхности вертикального цилиндра радиусом 15 м. Центр масс мотоцикла с человеком отстоит на 1 м от места соприкосновения колес со стенкой. Коэффициент трения шин о стенки 0,5. Определите: 1) минимальную скорость, с которой должен ехать мотоциклист; 2) угол наклона мотоциклиста к горизонтальной поверхности при данной минимальной скорости.
A. [1) 17,1 м/с; 2) 26°34'] B. [1) 1,71 м/с; 2) 16°34']
C. [1) 17,1 м/с; 2) 6°34'] D. [1) 1,71 м/с; 2) 26°34']
2.35. Шар массой 10 кг сталкивается с шаром массой 4 кг. Скорость первого шара 4 м/с, второго 12 м/с. Найти общую скорость шаров после удара в двух случаях: когда малый шар нагоняет большой шар, движущийся в том же направлении, и когда шары движутся навстречу друг другу. Удар считать прямым, центральным, неупругим.
А. [6,29 м/с; 0,57 м/с] В. [9,7 м/с; 0,57 м/с]
С. [6,29 м/с; 7,4 м/с] D. [0,57 м/с; 6,29 м/с]
2.36. Человек, стоящий в лодке, сделал шесть шагов вдоль лодки и остановился. На сколько шагов передвинулась лодка, если масса лодки в два раза больше массы человека или в два раза меньше?
А. [2 шага; 4 шага] В. [1 шаг; 4 шага]
С. [2 шага; 2 шага] D. [1 шаг; 2 шага]
2.37. В лодке массой 240 кг стоит человек массой 60 кг. Лодка плывет со скоростью 2 м/с. Человек прыгает с лодки в горизонтальном направлении со скоростью 4м/с относительно лодки. Найти скорость лодки после прыжка человека: а) вперед по движению лодки; б) в сторону, противоположную движению лодки.
А. [1м/с; 3 м/с] В. [3м/с; 1м/с]
С. [3,5 м/с; 4,5 м/с ] D. [1 м/с; 4,5м/с]
2.38. Из пружинного пистолета вылетела пулька, масса которой 5 г. Жесткость пружины 1,25 кН/м. Пружина была сжата на 8 см. Определите скорость пульки при вылете ее из пистолета.
А. [40 м/с] В. [1,3 м/с]
С.[16 м/с] D. [4 м/с]
2.39. Шар массой 200 г, движущийся со скоростью 10 м/с, ударяет неподвижный шар массой 800 г. Удар прямой, центральный, абсолютно упругий. Определите проекции скоростей шаров после удара. (Направление оси выбрать по движению первого шара до удара).
А. [- 6 м/с; 4 м/с] В. [2 м/с; 2 м/с]
С. [7,6 м/с; 4 м/с] D. [6 м/с; - 4 м/с]
2.40. Струя воды сечением 6 см2 ударяет о стенку под углом 60° к нормали и упруго отскакивает от стенки без потери скорости. Найти силу, действующую на стенку, если известно,






