Далее реализуем примеры работ 1 (часть 1), 2 (с пятью и шестью видами продукции) в MatLab с контрольной проверкой по результатам моделирования в Excel

3. Показать работу преподавателю и оформить отчет.

 

1. Титульный лист (пример приведен на следующей странице).

2. Введение (цель работы, основные положения).

3. Задание (задача).

4. Способ решения поставленной задачи (математические формулы).

5. Схема компьютерной модели.

6. Результаты решения (числовые результаты, экранные формы, графики).

7. Выводы по работе.

 

Литература

 

1. Дьяконов В. MatLad 6/6.1/6.5 SIMULINK 4/5 основы построения. М.: СОЛОН-Пресс, 2002. 768 с.

2. Черных И.В. SIMULINK среда создания инженерных приложений. Ь.: МИФИ, 2003. 496 с.

Лабораторная работа 5 (4 часа)

 

Цель: научиться решать задачи ДЛП (выражения (2.52) - (2/63) введения) и перехода на выпуск новой продукции в программном продукте MatLab.

 

 

ЗАДАНИЕ

 

Процесс планирования осуществляется обычно задолго до плана выполнения.

Будем разрабатывать оптимальный план с использованием задачи (статического) линейного программирования.

При переходе к рынку условия реализации плана могут меняться в процессе его выполнения:

при изменении спроса на выпускаемую продукцию;

при оперативном переходе на выпуск новой продукции.

Здесь используется аппарат динамического линейного программирования. Метод описания многоуровневой системы, базирующийся на этом аппарате, называется однородным.

А. Задача СЛП.

Взять программу lp13 примера 1 работы 4 и поставить в комментарии (% перед началом строки программы) строку f=…. Открыть файл моделирования (File-New-Model). Открыть SIMULNK (синий значок). В открывшееся окно поместить из пакета SIMULINK в горизонтальный ряд элементы Constant из набора Source, Matlab Fcn из User-Defined Function Display из Sinks и соединить их последовательно с помощью мыши (рис. 1).

 

1. «Кликнуть» компонент Constant и в установившемся заставке установить в окне Constant Value значение [-5 -4 -6], нажать кнопку Apply и закрыть заставку. В компоненте Matlab Fcn в окне в окне MatLab function установить lp13(u), нажать кнопку Apply и закрыть заставку.

В заставке untitled* запустить программу, нажав на панели инструментов «треугольник» или Simulation-Start.

В дисплее (растянуть его по вертикали) получится решение для статического плана.

 

 

Рис. 1. Решение задачи линейного программирования в Optimization Toolbox

 

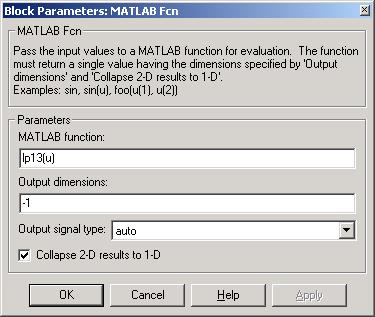
Рис. 2. Результат решения задачи линейного программирования

 

Б. Задача ЖЛП.

2. Чтобы получить динамический план, следует вместо дисплея добавить динамическое звено. Пусть общий интервал моделирования t=10, а минимальный интервал t1=0,1.

Введем с помощью «размножителей» Mux и Demux три инерционных элемента первого порядка (рис 3 из Continuous – Nransfer Fcn).

 

 

Рис. 3. Линейное программирование и разомкнутая система управления

(вход-выход)

 

На выходе поставим осциллограф Sinks - Scope. Запустим схему, «кликнем» на элементе Scope и получим результат (рис. 4).

 

 

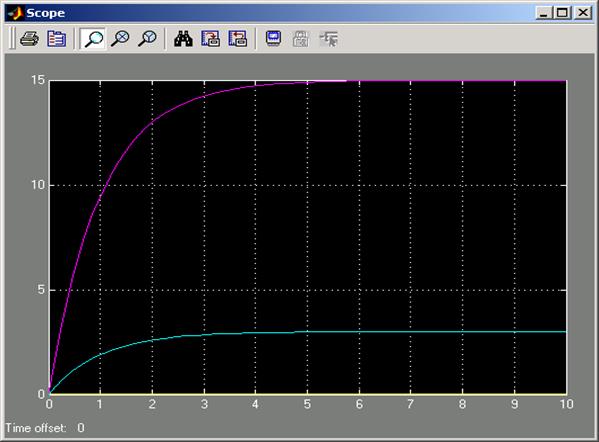
Рис. 4. Переходный процесс при планировании

 

3. Переставить элементы Transfer Fcn и MatLab Fcn и провести работы п.2. Сравнить результаты с п. 2.

4. Проделать п. 2 для части 1 работы 1.

5. В тех же примерах п. 2 и 4 заменить элементы Transfer Fcn на элемент Continuous – State Space и задайте матрицы A, B, C единичными, а матрицу D – нулевой и повторить примеры.

6. Оптимизационное звено должно содержать элемент Matlab Fcn с программой linprog из раздела Optimization Toolbox пакета Simulink, входящего в состав программного продукта MatLab.

Недостатком такого звена является многократное повторение операции в элементе Matlab Fcn. Чтобы повторения исключить, в элемент Constant вводят результаты выполнения программы оптимизации lp13, а элемент Matlab Fcn убирают (рис. 5).

Для этого в программе или рабочем пространстве выполняется команда

>> UU=lp13

Optimization terminated successfully.

Оптимизация осуществляется в функции lp13.

function x= lp13(f,A,b,lb);

f=[-5; 4; -6];

A=[1 1 1; 3 2 4; 3 2 0];

b=[20; 42; 30];

lb=zeros(3,1);

[x]=linprog(f,A,b,[],[],lb)

Запустить схему и убедиться, что оптимизация проходит один раз.

В. Переход на выпуск новой продукции.

7. В самом общем случае модель процесса перехода на выпуск новой продукции может быть представлена рис. 5, а переходные процессы отражены на рис. 6 и рис. 7.

 

 

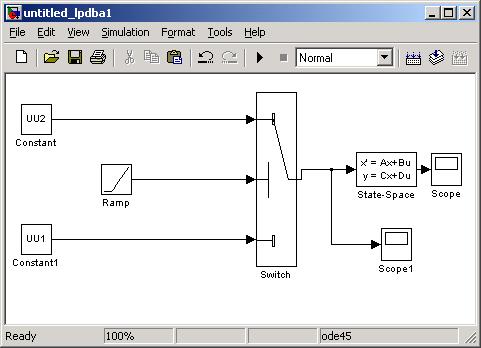
Рис 5. Качественное изменение плана (новая продукция)

 

 

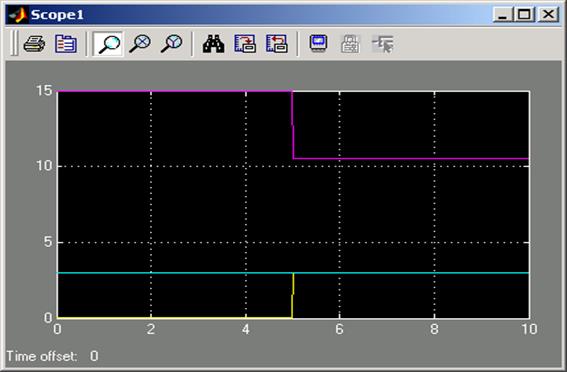
Рис. 6. Изменение плана при появлении новой продукции

 

 

Рис. 7. Планирование при появлении новой продукции

 

На рис. 5 выделяются следующие составляющие: оптимизационное звено; переключатель; инерционная составляющая.

На рис. 5 в качестве функций Matlab Fcn выступают nlp2 (вверху) и nlp1.

 

function x= nlp2(f,A,b,lb);

f=[-5; -4; -6];

A=[1 1 1; 3 2 4; 3 2 0; 1 0 0; 0 1 0; 0 0 1];

b=[20; 42; 30; 3; 16; 4];

lb=zeros(3,1);

[x]=linprog(f,A,b,[],[],lb);

 

function x= nlp1(f,A,b,lb);

f=[-5; -4; -6];

A=[1 1 1; 3 2 4; 3 2 0];

b=[20; 42; 30];

lb=zeros(3,1);

[x]=linprog(f,A,b,[],[],lb);

 

UU1=nlp1

Optimization terminated successfully.

 

UU1 =

 

0.0000

15.0000

3.0000

 

>> UU2=nlp2

Optimization terminated successfully.

 

UU2 =

 

3.0000

10.5000

3.0000

 

Переключатель (рис. 5) может быть автоматическим или ручным. В первом случае (рис. 5) в элементе Source – Ramp установить наклон линейной функции (slope) равным 1, а в элементе Signal Routing - Switch - параметр threshold равным 5. При интервале времени моделирования в 10 единиц ключ Switch сработает при значении времени 5.

Инерционная составляющая может быть реализована с использованием пространства состояний, как на рис. 5.

8. Реализовать, как в п. 7, примеры работы 2 (с пятью и шестью видами продукции).

9. Показать работу преподавателю и оформить отчет.

 

1. Титульный лист (пример приведен на следующей странице).

2. Введение (цель работы, основные положения).

3. Задание (задача).

4. Способ решения поставленной задачи (математические формулы).

5. Схема компьютерной модели.

6. Результаты решения (числовые результаты, экранные формы, графики).

7. Выводы по работе.

 

Лабораторная работа 6 (4 часа)

 

Цель: научиться применять задачу СЛП в процедуре замены ресурсов в программном продукте Excel.

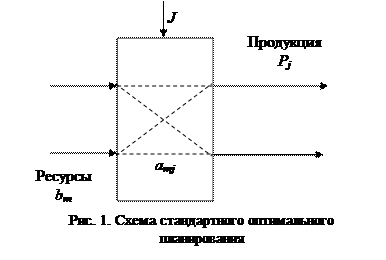
Основные положения. Пусть имеется задача оптимального планирования.

_J

S С_j P_j à max, (1)

^{j = 1}

_J

S d_mj P_j £ b_m, (2)

^{j = 1}

S_j ^­£ P_j £ S _j⁺, (3)

 

 

где в ограничениях по ресурсам и спросу, в целевой функциивведены обозначения P_j, b_m, S _j ­ вектор-столбцы искомого плана, ограничения (размерности J, j = 1, J), ресурсов размерности M (m = 1, M); d_mj ­ элементы матрицы размерности M× J норм расхода ресурсов; С_j ­ вектор-строка (размерности J) прибыли от выпуска единицы готовой продукции; G ­ целевая функция.

Схема этой задачи может быть представлена в виде рис. 1.

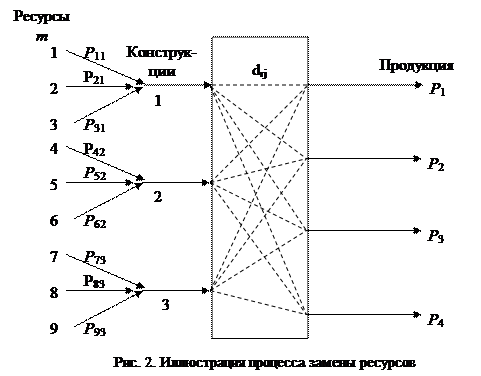
Предположим, что имеется возможность замены дефицитного ресурса на другие разновидности ресурса с похожими свойствами. На рис 2, например, ресурс m =1 может быть заменен на ресурсы m = 2 и m = 3. Наборы подобных (в данном случае трех) ресурсов будем называть конструкциями r (r = 1, R).

Если ресурс m = 1 использован полностью, а требуется дополнительное количество ресурса, то вводят ресурс m = 2 и т.д. Правило замены определяется предпочтениями П _mr для соответствующего ресурса.

Тогда задача замены ресурса математически может быть описана выражениями (1), (3), к которым добавляются выражения

 

 

_J

S d_rj P_j £ P_r, (4)

^{j = 1}

_M

P_r = S P_mr, (5)

^{m = 1}

_R

S P_mr £ b_m, (6)

^{r = 1}

_{R M}

F = S S П _mr P_mr à min. (7)

^{r = 1 m = 1}

где r = 1, R – конструкция (совокупность заменяющих ресурсов); P_r, P_mr – соответствующие планы; П_mr – приоритет ресурса m в конструкции r, a_rj – норма расхода; b_m – наличное количество ресурса.

 

Нетрудно заметить, что задача замены является векторной (двухкритериальной) задачей линейного программирования. Ее решение возможно двумя способами:

1) двухшаговое решение: на первом шаге ­ решение задачи (1) ­ (3), на задачи втором ­ (4) ­ (7).

2) как непосредственно двухкритериальной задачи;

Иллюстрируем указанные способы на конкретном числовом примере.

Числовой пример. Пусть имеется задача со следующими числовыми данными в соответствии с рис. 2.

Производство выпускает четыре вида продукции j (j = 1, 4) для чего требуется три вида материальных ресурсов.

Каждый материальный ресурс состоит из трех заменяющих друг друга материалов (конструкций). Первый вид материала является предпочтительным из всех и имеет вес 1 (один), второй вид материала менее предпочтителен с весом 3 (три), третий вид материала наименее предпочтителен и имеет вес 5 (пять).

Нормы расхода ресурсов не зависят от вида материала в конструкции и определяются таблицей.

 

Продукция Ресурс

 

Выпуск продукции P_j ³ 0, P ₁ ³ 8, P ₃ ³ 5.

Основная целевая функция максимизируется по выпускаемой продукции P_j и имеет коэффициенты 60; 70; 120; 130.

Задача решается для трех интервалов времени t (t = 1, 3).

К началу первого интервала имеется следующее количество материалов

 

Интервал t	Конструкция	Материал	Количество

 

Материалы, израсходованные на данном интервале времени, выбывают из расчетов на последующих интервалах времени.

К началу интервалов t = 2 и t = 3 поступают дополнительные материалы в количествах, отраженных в табл. 1.

Решение задачи.

Обратимся к первому способу. На первом шаге первого интервала времени положим, что заменяемые ресурсы равноценны и наличное количество ресурсов определяется суммой ресурсов конструкции. Иными словами в соответствии с табл. 1 P ₁₁ + P ₂₁ + P ₃₁ = (10 + 15 + 7) = 32; P ₄₂ + P_{5 2} + P ₆₂ = 210; P ₇₃ + P ₈₃ + P_{9 3} = 180. Решается задача по программе

 

function x= lp1_osnov(f,A,b,lb,ub);

f=[­ 60; ­ 70; ­ 120; ­ 130];

A=[1 1 1 1; 6 5 4 3; 4 6 10 13];

b=[32; 210; 180];

lb=zeros(3,1);

ub=[8; 0; 5; 0];

[x]=linprog(f,A,b,[],[],lb,ub);

 

Решением служит (P ₁, P ₂, P ₃, P ₄) = (8, 0, 5, 0).

На втором шаге используется программа

 

function x= lp1_zamen(f,A,b,lb,ub);

f=[1; 3; 5; 1; 3; 5; 1; 3; 5];

A=[-1 -1 -1 0 0 0 0 0 0; 0 0 0 -1 -1 -1 0 0 0; 0 0 0 0 0 0 -1 -1 -1];

b=[-13; -68; - 82];

lb=zeros(9,1);

ub=[5; 6; 17; 30; 40; 212; 40; 100; 70];

[x]=linprog(f,A,b,[],[],lb,ub);

 

Решение второго шага совпадает с решения P_mr табл. 2.

Поскольку суммарных ресурсов больше, чем надо для оптимального плана, на этапах 2 и 3 решения (P ₁, P ₂, P ₃, P ₄) не меняются. Решения P_mr по заменам совпадают со значениями таблиц 3 и 4.

Используем второй способ. Зададим веса критериев G и F равными единице. Рассмотрим новый критерий H = ­ F + G, при котором двухкритериальная задача становится статической

 

­ 60 P ₁ ­ 70 P ₂ ­ 120 P ₃ ­ 130 P ₄ + P ₁₁ + 3 P ₂₁ + 5 P ₃₁ + P ₄₂ + 3 P ₅₂ + 5 P ₆₂ + P ₇₃ + 3 P ₈₃ + 5 P ₉₃ à min.

 

Ограничения имеют вид

P ₁ + P ₂ + P ₃ + P ₄ ­ P ₁₁ ­ P ₂₁ ­ P ₃₁ ≤ 0

6 P ₁ + 5 P ₂ + 4 P ₃ + 3 P ₄ ­ P ₄₂ ­ P_{5 2} ­ P ₆₂ ≤ 0

4 P ₁ + 6 P ₂ + 10 P ₃ + 13 P ₄ ­ P ₇₃ ­ P ₈₃ ­ P9 ₃ ≤ 0

 

P ₁ ³ 0, P ₂ ³ 0, P ₃ ³ 0, P ₄ ³ 0, P_mr ³ 0, m = 1, 9; r = 1, 3,

P ₁ ≤ 8, P ₃ ≤ 5, b ₁ = 16, b ₂ = 110, b ₃ = 100, P ₁₁ ≤ 10, P ₂₁ ≤ 15, P ₃₁ ≤ 7, P ₄₂ ≤ 110,

P_{5 2} ≤ 10 P ₆₂ ≤ 90, P₇₃ ≤ 100, P ₈₃ ≤ 30, P ₉₃ ≤ 50/

 

Таблица 1

Поступление ресурсов

Интервал t	Конструкция	Материал	Количество

 

Перейдем к решениям на соответствующих интервалах времени, используя пакет MatLab.

Программа для интервала 1 имеет вид

 

function x= lp1_vect(f,A,b,lb,ub);

f=[1; 3; 5; 1; 3; 5; 1; 3; 5];

A=[-1 -1 -1 0 0 0 0 0 0; 0 0 0 -1 -1 -1 0 0 0; 0 0 0 0 0 0 -1 -1 -1];

b=[-16; -110; -100];

lb=zeros(9,1);

ub=[5; 6; 17; 30; 40; 212; 40; 100; 70];

[x]=linprog(f,A,b,[],[],lb,ub);

 

Полученные с ее помощью решения (P ₁, P ₂, P ₃, P ₄) = (8, 0, 5, 0). В табл. 2 показаны решения P_mr. В ней же указаны неиспользованные (остатки) ресурсов, передаваемые на следующий интервал времени, поступления и наличие ресурсов на следующем интервале времени.

 

Таблица 2

Этап 1

Решения Pmr	Остаток	Поступления	Наличие ресурсов

 

Отметим, что ресурсы b ₁, b ₃ расходуются полностью,а b ₂ частично.

На этапах 2 и 3 решения задачи (1) ­ (3) не меняется, изменяются данные по заменяемым ресурсам (табл. 1), а значения P_mr приведены в табл. 3 и табл. 4.

 

Таблица 3

Этап 2

Решения Pmr	Остаток	Поступления	Наличие ресурсов

 

 

Таблица 4

Этап 3

Решения Pmr	Остаток	Поступления	Наличие ресурсов

 

Данные способы могут быть распространены на замену нематериальных ресурсов (трудовых ресурсов, оборудования) с той лишь особенностью, что неиспользованные ресурсы теряются.

 

Литература

1. Чертовской В.Д. Интеллектуализация автоматизированного управления производством. СПб.: Изд-во С.-Петерб. ун-та, 2007. 164 с.

2. Чертовской В.Д. Информационные технологии в исследовании процесса управления производством //Журнал университета водных коммуникаций, 2010, вып. 1. С. 123-128.

3. Альсевич В.В., Габасов Р, Глушенков В.С. Оптимизация линейных экономических моделей. Статические задачи. Мн.: БГУ, 2000. 210 с.

 

 

ЗАДАНИЕ

 

ЗАДАЧА ЗАМЕНЫ РЕСУРСОВ

 

1. Решить задачу замены ресурсов с использованием пакета Excel.

Производство выпускает четыре вида продукции j (j = 1, 4) для чего требуется три вида материальных ресурсов.

Каждый материальный ресурс состоит из трех заменяющих друг друга материалов (конструкций). Первый вид материала является предпочтительным из всех и имеет вес 1 (один), второй вид материала менее предпочтителен с весом 3 (три), третий вид материала наименее предпочтителен и имеет вес 5 (пять).

Нормы расхода ресурсов не зависят от вида материала в конструкции и определяются таблицей.

 

Продукция Ресурс

 

Выпуск продукции P_j ³ 0, P₁ ³ 8, P₃ ³ 5.

Основная целевая функция максимизируется по выпускаемой продукции P_j и имеет коэффициенты 60; 70; 120; 130.

Задача решается для трех интервалов времени t (t = 1, 3).

К началу первого интервала имеется следующее количество материалов

 

t	Конструкция	Материал	Количество

 

Материалы, израсходованные на данном интервале времени, выбывают из расчетов на последующих интервалах времени. Оставшиеся материалы переходят в следующий интервал.

К началу интервалов t = 2 и t = 3 поступают дополнительные материалы в количествах, отраженных в таблице.

 

 

t	Конструкция	Материал	Количество

 

Показать работу преподавателю и оформить отчет..

 

1. Титульный лист (пример приведен на следующей странице).

2. Введение (цель работы, основные положения).

3. Задание (задача).

4. Способ решения поставленной задачи (математические формулы).

5. Схема компьютерной модели.

6. Результаты решения (числовые результаты, экранные формы, графики).

7. Выводы по работе.

 

Литература

 

1. Советов Б.Я., Цехановский В.В., Чертовской В.Д. Основы теории управления. СПб.: Политехника, 2008. 219 с.

2. Чертовской В.Д. Интеллектуализация автоматизированного управления производством. СПб.: 2007. 164 с.

3. Советов Б.Я., Цехановский В.В., Чертовской В.Д. Теоретические основы автоматизированного управления. М.: Высш. шк., 2006. 463 с.

4. Курицкий Б.Я. Поиск оптимальных решений средствами Excel 7.0. Спб.: BHV, 1997. 384 с.

 

Описать

 

ДЛП + ДЛП

7. управление