ЧАСТЬ 2.
Решения задачи может не быть (несовместность). Изменим немного решение примера А. Рекомендуется делать на листе 2.
Пример Б.
Целевая функция F = 60 p1 + 70 p2 + 120 p3 + 130 p4 à max
Трудовые p1 + p2 + p3 + p4 £ 16
Материалы 6 p1 + 5 p2 + 4 p3 + 3 p4 £ 110
Финансы 4 p1 + 6 p2 + 10 p3 + 13 p4 £ 100
p = {pj}, pj ³ 0, j = 1, 4;
17£ p1 £ 20; p 2 £ 5, p3 £ 6.
Рис. 2 получает вид, показанный на рис. 11.
При попытке решения на рис. 9 появится сообщение о несовместности задачи.
Чтобы получить решение, в ограничениях необходимы дополнительные ресурсы (ti, i = 1, 3). Для определения их минимального значения ti необходимо решить другую задачу линейного программирования.
Целевая функция F = 60 p1 + 70 p2 + 120 p3 + 130 p4 à max (7)
Трудовые p1 + p2 + p3 + p4 – t1 = 16 (8)
Материалы 6 p1 + 5 p2 + 4 p3 + 3 p4 – t2 = 110 (9)
Финансы 4 p1 + 6 p2 + 10 p3 + 13 p4 – t3 = 100 (10)
p = {pj}, pj ³ 0, j = 1, 4, tj ³ 0, j = 1, 3; (11)
p1 £ 10; p2 £ 5, p3 £ 6. (12)
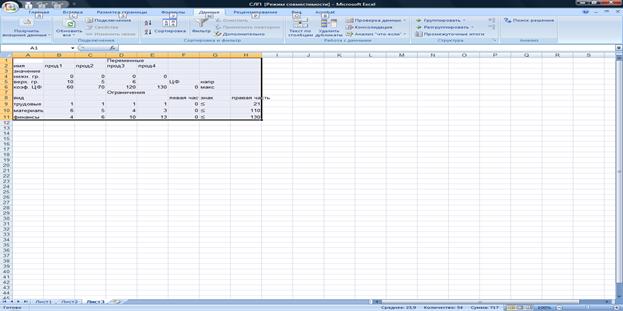
Рис. 11
Задача получает вид
F = t1 + t2 + t3 à min (13)
p1 + p2 + p3 + p4 – t1 = 16 (14)
6 p1 + 5 p2 + 4 p3 + 3 p4 – t2 = 110 (15)
4 p1 + 6 p2 + 10 p3 + 13 p4 – t3 = 100 (16)
p = {pj}, pj ³ 0, j = 1, 4; (17)
p1 = 10; p2 = 5, p3 = 6. (18)
tj ³ 0, j = 1, 3. (19)
1б. Интерфейс рис. 1 изменяется (рис. 12)
4б. Изменяются массивы рис. 4 в соответствии с выражениями (14) – (16).
7б, 8б. Изменяются ограничения в соответствии с выражениями (18) – (19): B3 = 10; C3 = 5; D3 = 6; H3 ³0; E3 ³0; F3 ³0; G3 ³0; I9£K9; I10£K10; I11£K11.
Решить задачу при новых условиях и найти ti.
Решение показать преподавателю.
Выполнить контрольную проверку с полученными числовыми значениями ti для примера В. Рекомендуется делать на листе 3.
Пример В.
F = 60 p1 + 70 p2 + 120 p3 + 130 p4 à max (7)
p1 + p2 + p3 + p4 = 16 + t1 (8)
6 p1 + 5 p2 + 4 p3 + 3 p4 = 110 + t2 (9)
4 p1 + 6 p2 + 10 p3 + 13 p4 = 100 + t3 (10)
p = {pj}, pj ³ 0, j = 1, 4, tj ³ 0, j = 1, 3; (11)
p1 £ 10; p2 £ 5, p3 £ 6. (12)

Рис. 12
ЧАСТЬ 3
Для закрепления материала решить одну из следующих задач по указанию преподавателя. Решение показать преподавателю.
Задача 1
F = p1 à max
p1 + p2 ³ 1
p = {pj}, pj ³ 0, j = 1, 2.
Задача 2
В примере А снять ограничения (6). В ячейке F6 (рис. 6) задать величину 1100. Найти величины pj и правых частей ограничений (2) – (4).
Задача 3
F = 2 p1 + 3 p2 à max
p1 + 2p2 £ 4
3 p1 + p2 £ 6
p = {pj}, pj ³ 0, j = 1, 2.
Задача 4
F = 2 p1 + 3 p2 à min
p1 + 2p2 £ 4
3 p1 + p2 £ 6
p1 + p2 £ 2,8
p = {pj}, pj ³ 0, j = 1, 2.
Задача 5
F = 4 p1 + 6 p2 à max
p1 + 3p2 = 2
2 p1 + p2 = 3
p = {pj}, pj ³ 0, j = 1, 2.
Задача 6
F = 4 p1 + 6 p2 + 2,8 p3 à min
p1 + 3p2 + p3 = 2
2 p1 + p2 + p3 = 3
p = {pj}, pj ³ 0, j = 1, 3.
Задача 7
F = p1 + p2 à max
2p1 + p2 £ 4
p1 + 2p2 £ 4
p = {pj}, pj ³ 0, j = 1, 2.
Задача 8
F = 4p1 + 4p2 à min
2p1 + p2 = 1
p1 + 2p2 = 1
p = {pj}, pj ³ 0, j = 1, 2.
Задача 9
F = p1 + 3p2 à max
p1 - p2 £ 3
- p1 + p2 £ 4
p = {pj}, pj ³ 0, j = 1, 2.
Задача 10
F = p1 + 3p2 + 2 p3 + p4 + p5à max
- p1 + 4p3 + 3p4 = 2
2p1 + 3p2 + 3p3 + 5p4 – p5 = 3
p1 + 3p2 + p3 + 2p4 + p5= 2
p1 + 3p2 + p3 + 2p4 + p5= 2
2p1 + 6p2 + 8p3 + 10p4 = 7
p = {pj}, pj ³ 0, j = 1, 5.
Задача 11
F = 5p1 - p2 - p3 + 2p4 + p5à max
2p1 + 6p3 + 4p4 - 3p5 = 2
- p1 + 3p2 + 7p3 – 2p5 = 1
p1 + p2 + 2p3 + p4 + 2p5= 1
p = {pj}, pj ³ 0, j = 1, 5.
Задача 12
F = p1 +3 p2 + 2p3 + 4p4 + p5à max
- p1 + 4p3 + 3p4 = 2
2p1 + 3p2 + 3p3 + 5p4 - 2p5 = 3
p1 + 3p2 + p3 + 2p4 + p5= 2
p = {pj}, pj ³ 0, j = 1, 5.
Задача 13
F = 3p1 - 4p2 + 2p3 à max
p1 + 2p2 + p3 £ 18
2p1 + p2 + p3 £ 16
p1 + p2 £ 8
p2 + p3 £ 6
p = {pj}, pj ³ 0, j = 1, 3.
Задача 14
F = 18p1 + 16p2 + 8p3 + 6p4à max
p1 + 2p2 + p3 ³ 3
2p1 + p2 + p3 + p4³ 4
p1 + p2 - p4³ 2
p = {pj}, pj ³ 0, j = 1, 4.
Задача 15
F = 3 p1 + p2 + p3 à max
2p1 + p2 + 3p3 £ 10
2 p2 + p3 £ 6
p = {pj}, pj ³ 0, j = 1, 3/
Задача 16
F = 10p1 + 6p2 à min
2p1 ³ 3
p1 + 2p2 ³ 1
3p1 + p2 ³ 1
p = {pj}, pj ³ 0, j = 1, 2.
Задача 17
F = p1 + 2p2 + 3 p3 - p4 à max
p1 + 2p2 + 3p3 = 15
2p1 + p2 + 5p3 = 20
p1 + 3p2 + p3 + 2p4 + p5= 2
p1 + 2p2 + p3 + p4 = 10
p = {pj}, pj ³ 0, j = 1, 4.
Задача 18
F = 3p1 + 2p2 + 5 p3 + 4p4 + 6p5à max
p1 +p3 + 3p4 = 2
2p1 + 3p2 + 3p3 + 5p4 – p5 = 3
p1 + 3p2 + p3 + p4 + p5= 100
20p1 + 30p2 + 35p3 + 30p4 + 40p5= 3000
40p1 + 20p2 + 60p3 + 35p4 + 25p5 = 4500
p = {pj}, pj ³ 0, j = 1, 5.
Задача 19
F = 4 p1 + 3 p2 à min
- p1 + p2 + p3 = 3
2 p1 + 3p2 - p4 = 12
p1 + 4p2 – p5 = 2
p = {pj}, pj ³ 0, j = 1, 5.






