Предварительные условия.Для решения задачи после открытия Excel необходимо перейти к элементам меню Данные - Поиск решения

ФЕДЕРАЛЬНОЕ АГЕНТСТВО МОРСКОГО И РЕЧНОГО ТРАНСПОРТА

 

ФЕДЕРАЛЬНОЕ бюджетное ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

 

«САНКТ-ПЕТЕРБУРГСКИЙ БЮДЖЕТНЫЙ УНИВЕРСИТЕТ ВОДНЫХ КОММУНИКАЦИЙ»

 

Кафедра вычислительных

систем и информатики

 

В.Д. Чертовской

 

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к лабораторным работам

 

по курсу «Теория информации»

 

Специальность

«Информационные системы и технологии»

 

Санкт-Петербург

ПРЕДИСЛОВИЕ

 

Перед выполнением комплекса лабораторных работ необходимо внимательно ознакомиться с данным предисловием.

 

Представленный комплекс лабораторных работ выполняется при обучении на 2-ом курсе.

Каждая работа рассчитана на 4 академических часа: 2 часа – постановка задачи и выполнение работы; 2 часа – отчет в электронном виде с защитой работы.

 

1. Титульный лист (пример приведен на следующей странице).

2. Введение (цель работы, основные положения).

3. Задание (задача).

4. Способ решения поставленной задачи (математические формулы).

5. Схема компьютерной модели.

6. Результаты решения (числовые результаты, экранные формы, графики).

7. Выводы по работе.

 

Отчет проверяется алгоритмом на плагиат.

Выполнение следующей работы возможно лишь после защиты предыдущей работы.

 

Пропуск двух лабораторных занятий влечет за собой изменение задания на более сложное более сложное задание

График выполнения работ

 

ФЕДЕРАЛЬНОЕ АГЕНТСТВО МОРСКОГО И РЕЧНОГО ТРАНСПОРТА

 

ФЕДЕРАЛЬНОЕ бюджетное ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

 

«САНКТ-ПЕТЕРБУРГСКИЙ БЮДЖЕТНЫЙ УНИВЕРСИТЕТ ВОДНЫХ КОММУНИКАЦИЙ»

 

 

Кафедра вычислительных

Систем и информатики

 

ОТЧЕТ

по лабораторной работе №

 

по курсу «Теория информации»

 

Выполнил

студент группы ИС(№)

 

(фамилия, инициалы)

 

Принял

 

Санкт-Петербург

 

ВВЕДЕНИЕ

 

Цель: комплекса лабораторных работ - ознакомиться с сутью и сферами применения, получить навыки использования задач программирования в процессах планирования и управления.

Общие положения. Автоматизированные системы управления предприятиями появились в 60-е годы XX века. Для них характерно, что в векторе спроса (плана) на продукцию менялась лишь величина составляющих, тогда как состав вектора не менялся.

Укрупненная подсистемная структура такой системы может быть представлена как трехуровневая (рис. 1). Производство в ней обведено штриховой линией.

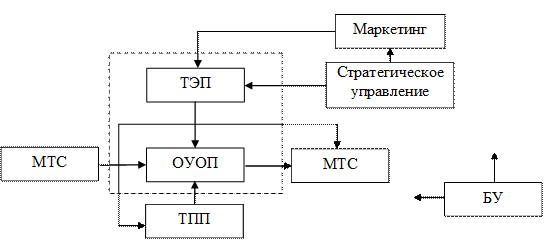
Рис. 1. Укрупненная схема связей функциональных подсистем
при рыночных отношениях: ТЭП – технико-экономическое планирование;
ОУОП оперативное управление основным производством; p
МТС – материально-техническое снабжение и сбыт;
ТПП – техническая подготовка производства; БУ – бухгалтерский учет

 

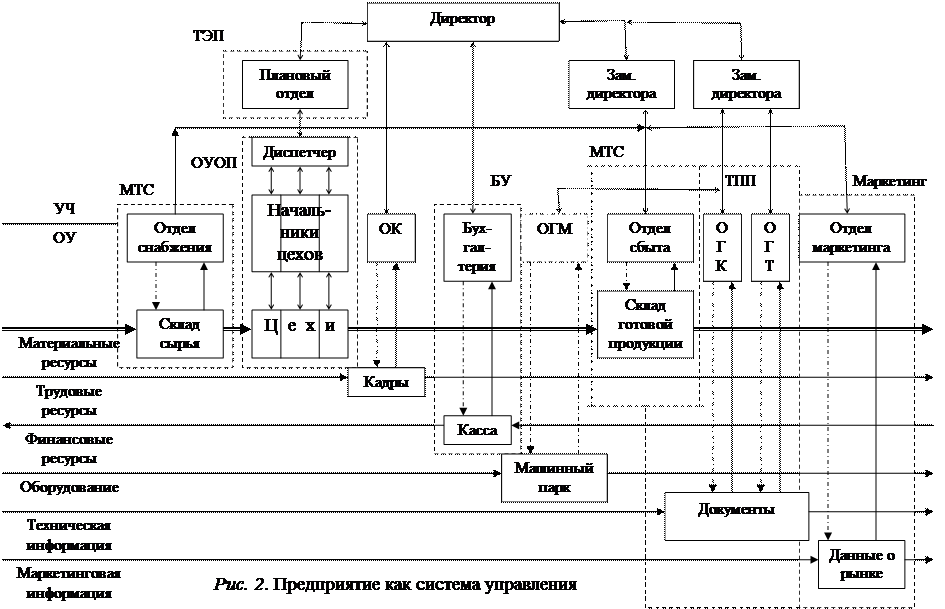
Эта структура получена из схемы предприятия как системы управления (рис. 2).

В таких традиционных системах управления спрос может быть представлен в виде

R ₃(t) = R ₃₀ - D R ₃ · 1(t – q), (1.1)

где R ₃₀ – прежний спрос; D R ₃ – количественное изменение спроса; q – момент изменения спроса; t – время; 1(t) – единичная функция.

При переходе к рынку возникла необходимость для достижения конкурентного преимущества оперативно переходить на выпуск новой продукции. Это означало, что в процессе эксплуатации системы менялись составляющие вектора спроса.

 

 

 

 

Добавлялись новые составляющие

R 4(t) = R 40 · 1(t – q), (1.2)

где R 4(t) – величина спроса на новую продукцию вида; q – момент возникновения спроса. При этом часть старой продукции могла сниматься с производства.

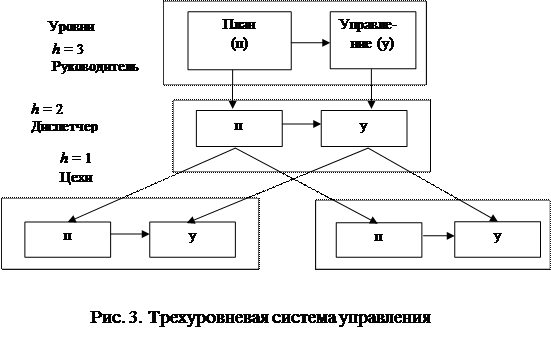
Потребовалось создание адаптивных автоматизированных систем управления производством, компенсация качественного изменения спроса в которых производилась путем изменения структурных связей в производстве. Структура рис. 1 удобнее при этос представить как трехуровневую (рис. 3).

 

 

В описании таких систем выделяются следующие этапы.

1. Описание отдельного структурного элемента без учета специфики уровня.

2. Описание отдельного структурного элемента с учетом специфики уровня.

3. Взаимодействие элементов.

Далее будет рассматриваться только первый этап.

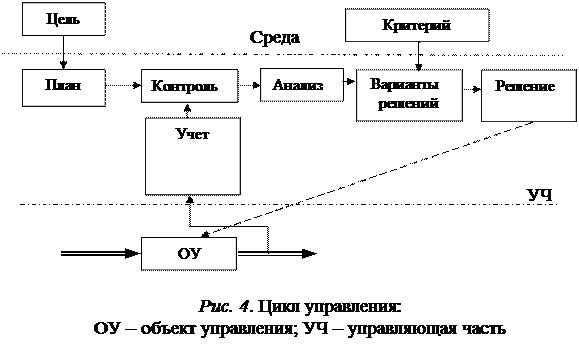
Каждый структурный элемент этой структуры характеризуется циклом управления (рис. 4), в котором процесс планирования становится относительно самостоятельным.

В математическом описании системы с такой структурой возможно использовать два метода: интегральный и однородный.

В интегральном методе процесс планировании описывается с помощью широко распространенного статического линейного программирования (СЛП), а процесс управления – с помощью метода линейно-квадратичной оптимизации (ЛКО).

 

 

Процесс планирования.

При планировании производства часто решают задачу оптимизации с помощью статического линейного программирования (СЛП).

DP [t] £ b (t), (2.16)

R ^-[t] £ P [t] £ R ⁺[t], (2.17)

G (P [t]) = FP [t] à max, (2.18)

где Р, b, R ­ вектор-столбцы искомого плана, наличного количества ресурсов, спроса; А ­ матрица норм расходов ресурсов; F ­ вектор-строка прибыли за единицу готовую продукцию; G – целевая функция; t ­ интервал времени.

Процесс управления.

В процессе управления, который удобно показать в непрерывной форме, выделяется описание объекта управления и управляющей части.

Объект управления

_.

z (t) = Az (t) + Bu (t), z (0) = z ₀, (2.51)

y (t) = Cz (t), (2.35)

управляющая часть

e (t) = P (t) — y (t), (2.36)

_T

J = 0,5{ e ^T (T) Se (T) +ò{ e ^T (t) Q e(t) ++ u ^T (t) Ru (t)} dt à min, (2.37)

⁰

В однородном методе оба процесса описываются с помощью задачи динамического линейного программирования (ДЛП), состоящей из задачи СЛП и системы разностных уравнений.

Процесс планирования в нем (рис. 5) описывается следующим образом

P (T) ³ R (T), (2.52)

P (t_i) = P (t_{i- 1}) - p (t_i), (2.53)

z (t_i) = Az (t_{i- 1}) + Bp ₁(t_{i- 1}), z (0) = z ₀,

i = 1, N, t_i = iv, t ₀ = 0, T = Nv, (2.54)

p (t_i) = Cz (t_i), (2.55)

Dp ₁(t_i) £ b (t_{i- 1}), (2.57)

G = - FP (T) à min, (2.58)

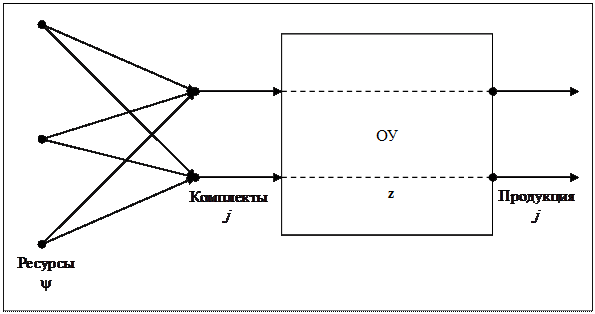где z – незавершенное производство; p ₁ – запуск комплекта материалов в производство; A, B, C - матрицы соответствующих размерностей; T, v - интервалы времени. Напомним, что под комплектом материалов понимается набор ресурсов, необходимый для выпуска единицы готовой продукции.

Рис. 5. Иллюстрация процесса планирования

 

Для описания процесса управления задача немного трансформируется.

Объект управления системы может быть представлен как

z (t_i) = Az (t_{i- 1}) + Bu (t_{i- 1}), (2.59)

y (t_i) = Cz (t_i), (2.60)

Du (t_i) £ b (t_i-1). (2.61)

Управляющая часть

e (t_i) = p (t_i) – y (t_i), (2.62)

_N

J = S{ C ₁ e (t_i) + C ₂ u (t_i)} à min, (2.63)

^{i =0}

где С ₁, С ₂ – вектор-строки стоимостей потерь за счет отклонения от плана и потребностей в дополнительных ресурсах для управления; e (t) = p (t) – y (t) вектор отклонений; T, v - интервалы времени; i = 1, N; T = Nv.

Задачи динамического линейного программирования вида (2.52) – (2.58) могут быть сведены к задаче статического линейного программирования, если для P (T) из выражения (2.53) использовать выражения (2.54) –(2.55). Тогда получим

P (T) = a₀ z (0) + a₁ p ₁(0) + a₂ p ₁(2) + … + a _N -₁ p ₁(N -2) + a _N p ₁(N -1), (2.64)

где

_{N N - s}

a₀ = С S A ⁱ_, a_s = С S A ⁱ B, s = 1, N. (2.65)

^{i = 1 i = 0}

Предлагаемый цикл лабораторных работ представляет компьютерную реализацию отдельного структурного элемента адаптивной автоматизированной системы управлении и включает выполнение задач СЛП, ДЛП, ЛКО.

Задача ЛКО решается с использованием электронных таблиц Excel.

Задачи линейного программирования могут решаться с использованием различных программных продуктов. В рассматриваемых работах применяются электронные таблицы Excel, комплекс MatLab иногда с пакетом SIMULINK.

 

Состав комплекса.

Лабораторная работа 1 (6 часов) - решение задачи СЛП в Excel.

Лабораторная работа 2 (6 часов) составление и решение разных задач СЛП в Excel.

Лабораторная работа 2 (4 часа) решение задачи ЛКО в Excel.

Лабораторная работа 4 (2 часа) задачи СЛП в MatLab.

Лабораторная работа 5 (4 часа) задачи СЛП, ДЛП и перехода на выпуск новой продукции в MatLab.

Лабораторная работа 6 (4 часа) задача замены ресурсов в Excel.

 

Оформление результатов работ. По завершении каждой работы студент представляет отчет в электронном виде. Все отчеты последовательно помещаются в одну папку с названием (именем) по фамилиям студентов.

Отчет (файл) работы должен иметь следующие составляющие.

1. Титульный лист.

2. Введение (цель работы, основные положения).

3. Задание (задача).

4. Способ решения поставленной задачи (математические формулы).

5. Схема компьютерной модели.

6. Результаты решения (числовые результаты, экранные формы, графики).

7. Выводы по работе.

 

 

РАЗДЕЛ 1. Решение задач с помощью Excel.

 

Лабораторная работа 1 (6 часов)

 

Цель работы. Познакомиться с сутью, областью применения и реализацией задачи СЛП при наличии и отсутствии решения в программном продукте Excel.

 

Основные сведения.

 

Задача СЛП используется для описания процесса оптимального планирования. Это задача (2.16) - (2.18) во введении, т. е. задача планирования при использовании интегрального метода.

Пример 1.1. Примем обозначения: j = 1, J – вид выпускаемой продукции; (T) и [T] момент и интервал времени (например, месяц); P_j[T] – определяемый план; a_yj, y = 1, Y - норма расхода ресурса вида y на единицу продукции вида j; - наличное и резервное количество ресурса вида y; R_j^-[T] и R_j⁺[T] - нижняя и верхняя граница выпуска, величины которых определяются позднее; С_j – прибыль от выпуска единицы продукции. Тогда задача составления оптимального плана имеет вид

 

R_j^-[T] <= P_j[T] <=R_j⁺[T], j = 1, J (1.1)

_J

Sa_yjP_j[T] <= b_y(0) {+ f_y(0)} (1.2)

^{j = 1}

_J

G = SC_j P_j[T] à max. (1.3)

^{j = 1}

Первые два выражения отражают ограничения, последнее – целевую функцию.

Будем называть эту форму записи свернутой.

Возможны развернутая и векторн-матричная форма этой задачи.

Развернутая форма.

R₁^-[T] <= P₁[T] <=R₁⁺[T],

…

R_J^-[T] <= P_J[T] <=R_J⁺[T],

a₁₁P₁[T] + a₁₂P₂[T] + … + a_1JP_J[T] ≤ b₁(0)

_…

a_Y1P₁[T] + a_Y2P₂[T] + … + a_YJP_J[T] ≤ b_Y(0)

C₁P₁[T] + C₂P₂[T] + … + C_JP_J[T] à max.

Векторно-матричная форма.

R^-[T] <= P[T] <=R⁺[T]

AP[T] <= b

CP à max,

 

где P[T] = (P₁[T] P₂[T] … P_J [T])^T, R[T] = (R₁[T] R₂[T] … R_J[T])^T, b = (b₁(0) b₂(0) … b_Y(0)) ^T, C = (C₁ C₂ … C_J),

A =	a11	a12	…	a1J
a21	a22	…	a2J
…	…	…	…
aY1	aY2	…	aYJ

 

 

ЗАДАНИЕ

 

Задание состоит из тех частей: в первой части рассматривается задача, имеющая решение, во второй задаче решения нет и требуется найти условия появления решения, третья часть предназначена для закрепления материала.

После завершения работы оформить отчет в электронном виде (см. предисловие).

Литература

 

Курицкий Б.Я. Поиск оптимальных решений средствами Excel 7.0 в примерах. СПб.: БХВ, 1997.384 с.

 

СТАТИЧЕСКОЕ ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ

 

ЧАСТЬ 1

Предварительные условия.Для решения задачи после открытия Excel необходимо перейти к элементам меню Данные - Поиск решения.

Если нет элемента Поиск решения, то его необходимо создать по такому алгоритму.

1. Щелкните значок Кнопка Microsoft Office, а затем щелкните Параметры Excel.

2. Выберите команду Надстройки, а затем в окне Управление выберите пункт Надстройки Excel.

3. Нажмите кнопку Перейти.

4. В окне Доступные надстройки установите флажок Поиск решения и нажмите кнопку ОК.

Совет. Если Поиск решения отсутствует в списке поля Доступные надстройки, чтобы найти надстройку, нажмите кнопку Обзор.

В случае появления сообщения о том, что надстройка для поиска решения не установлена на компьютере, нажмите кнопку Да, чтобы установить ее.

5. После загрузки надстройки для поиска решения в группе Анализ на вкладке Данные становится виден Поиск решения.

Теперь можно приступать к решению задачи.

Все результаты запомнить, поскольку они будут использованы в последующих работах для контроля результатов в программном продукте MatLab.

Постановка задачи. Решить на программном продукте Excel задачу статического линейного программирования в соответствии с примером

 

Пример А.

Целевая функция F = 60 p₁ + 70 p₂ + 120 p₃ + 130 p₄ à max (1)

 

Трудовые p₁ + p₂ + p₃ + p₄ £ 16 (2)

 

Материалы 6 p₁ + 5 p₂ + 4 p₃ + 3 p₄ £ 110 (3)

 

Финансы 4 p₁ + 6 p₂ + 10 p₃ + 13 p₄ £ 100 (4)

 

p = {p_j}, p_j ³ 0, j = 1, 4; (5)

 

p₁ £ 10; p₃ £ 6. (6)

Этапы решения задачи. Установка поиска решения.

Ввод исходных данных (с формированием интерфейса пользователя).

1. Первоначально создается интерфейс пользователя, показанный на рис. 1.

 

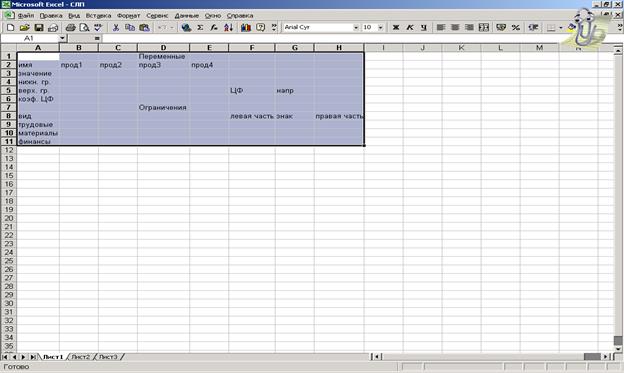
Рис. 1

 

2. Затем проводится заполнение интерфейса числовыми данными из примера (рис. 2).

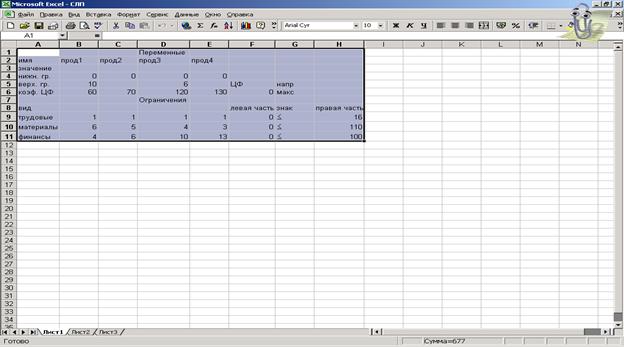
Рис. 2

 

3. Набрать выражение для целевой функции (1) в ячейке F6, для чего использовать функцию Сумма произведений (СУММПРОЗВ) – рис. 3.

 

 

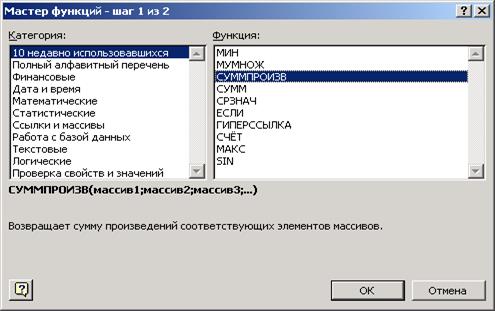
Рис. 3

 

4. После нажатия кнопки Ок ввести данные о целевой функции (рис. 4).

 

 

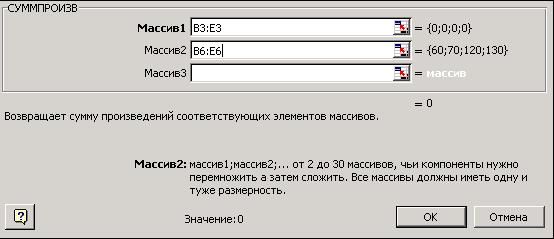
Рис. 4

 

Для удобства введения можно нажимать красную стрелку, что приведет к сворачиванию формы (рис. 5), и выделению соответствующих ячеек. Затем следует снова нажать красную стрелку, чтобы вернуться к рис. 4.

 

 

Рис. 5

 

5. Аналогично набираются выражения (2) - (4) в ячейках F9, F10, F11.

6. Открыть диалоговое окно Поиск решений (рис. 6). Установить целевую ячейку $F$6. Определить вид оптимизации (Максимальное или минимальное значение). Ввести адреса искомых переменных (изменяя ячейки) $B$3:$E$3.

 

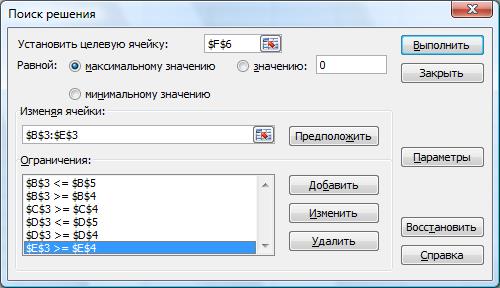
Рис. 6

 

7. Нажать кнопку Добавить. Откроется окно на рис. 7. Ввести ограничения (5), (6) – рис 7.Указать, например, «левую» ячейку $B$3, знак ограничения ³ и «правую» ячейку $B$4. Нажать кнопку Добавить. При ошибках введения воспользоваться кнопками Изменить и Удалить (рис. 6).

8. Аналогично ввести ограничения (2) – (4): $F$9£$H$9, $F$10£$H$10, $F$11£$H$11.

 

 

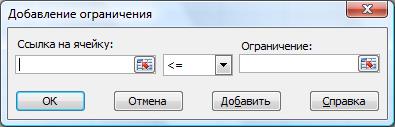
Рис. 7.

 

Выполнение задачи. 9. После ввода последнего ограничения нажать кнопку Ок или x. Происходит возврат в окно рис. 6 с указанием ограничений.

В окне рис. 6 нажать кнопку Параметры и откроется окно рис. 8.

 

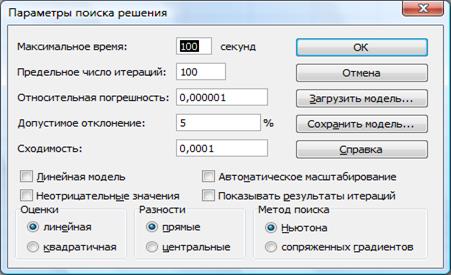
Рис. 8

 

Установить Максимальное время 100 секунд, Предельное число итераций 100, Относительная погрешность 0;000001, Допустимое отклонение – 5 %, Линейная (оценка), Прямые (производные), Ньютона (метод). Нажать кнопку Ок и вернуться к рис. 6. Нажать кнопку Выполнить. Появляется заставка – рис. 9.

 

Рис. 9

Получится решение – рис. 10.

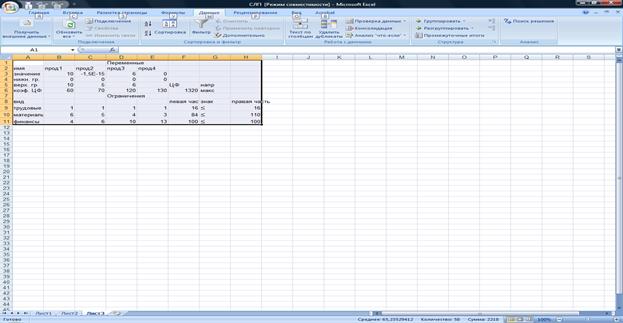
Рис. 10