Пусть функции f1(x, y) и f2(x, y) непрерывны в точках дуги АВ гладкой кривой, заданной уравнением у = j(х), где х Î[a, b].
Интегральной суммой для функций f1(x, y) и f2(x, y) по координатам называют сумму вида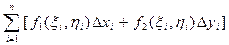 
(8.4),
где Dхi и Dyi – проекции элементарной дуги Ds на оси Ох и Оу.
Криволинейным интегралом по координатам от выражения
f1(x, y)dx + f2(x, y)dy по направленной дуге АВ называется предел интегральной суммы (8.4) пр и условии, что maxDxi ® 0 и maxDуi ® 0:
(8.5)
Рассмотрим основные свойства криволинейного интеграла второго рода.
1. Криволинейный интеграл второго рода меняет знак на противоположный при изменении направления пути интегрирования:
(это можно связать с тем, что в отличие от Dsi > 0, Dxi и Dyi могут быть и больше и меньше нуля).
2. Криволинейный интеграл второго рода равен сумме таких же интегралов по каждой из координат в отдельности:
.
Другие свойства аналогичны свойствам интеграла первого рода.
Криволинейный интеграл второго рода может быть вычислен по формуле: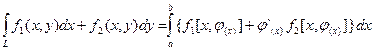 
(8.6).
Аналогичная формула используется, если требуется вычислить криволинейный интеграл второго рода по пространственной кривой
. В этом случае (и во многих случаях плоской кривой) целесообразно использовать параметрическое задание кривой.
Пример: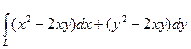 
, где L – дуга параболы у = х2, от точки А(–1; 1) до точки В(1; 1). у = j(х) = х2 и j`(х) = 2х. По формуле (8.6)
.
Криволинейный интеграл II рода численно равен работе, совершаемой переменной силой `F = `if1(x, y) + `jf2(x, y) на соответствующем криволинейном пути АВ.
Формула Грина. Это важное во многих приложениях соотношение позволяет установить связь между двойным интегралом по некоторой плоской области D и криволинейным интегралом второго рода по границе L этой области. Если функции f1(x, y) и f2(x, y) вместе со своими частными
производными 
и 
непрерывны в замкнутой области D (включающей границу L), то справедливо соотношение 
(8.7)
называемое формулой Грина. (Символ 
означает криволинейный интеграл по
замкнутому контуру). Двойной интеграл в (8.7) вычисляется, как обычно, сведением его к двукратному. Использование (8.7) позволяет во многих случаях существенно упростить решение задачи.
Тесты
3.21. Область Д является правильной:
1) по оси Ох;
2) по оси Оу;
3) правильной.
3.22. Область Д ограничена линиями 
; 
; 
. 
1) 
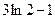; 2) 
; 3)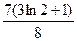 
.
3.23. Дан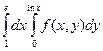 
. Изменив порядок интегрирования получим:
1) 
; 2) 
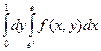; 3) 
.
3.24. Объем тела, ограниченного поверхностями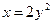 
, 
, 
, 
, составит (куб.ед)
1) 
; 2) 8; 3) –3; 4) 
.
3.25. Область V ограничена поверхностями х = 0, х = 2, у = 0, у = 3, z = 0, z = 4, 
1) 696; 2) 382; 3) –154; 4) 232.
3.26. Объем тела, ограниченного поверхностями 
, 
составит (куб.ед):
1) 
; 2) 
; 3) 
.
3.27. Криволинейным интегралом I рода называют:
1) 
;
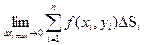2) 
;
3) 
.
3.28. На полукубической параболе 
лежат точки А(3; 2 
) и В(8; 
) 
1) 
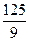; 2)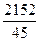 
; 3) - .
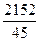3.29. Для криволинейного интеграла II рода 
справедливо:
1) = 
; 2) = - ;
3.30. Отрезок соединяет точки А(1; 1) и В(3; 4).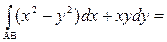 
1) 
; 2) 
; 3) 
; 4) 
.
