Двойной интеграл.Пусть функция f(x, y) определена в замкнутой ограниченной области D в плоскости хОу. Разобьем область D на n элементарных областей, имеющих площади DS1, DS2,…,DSnи диаметры d1, d2,…,dn. (Диаметром области называют наибольшее из расстояний между двумя точками границы этой области). Выберем в каждой элементарной области произвольную точку pi(xi, hi) и умножим значение функции в точке pi на площадь этой области. Интегральной суммой для функции f(x, y)по области D
называется сумма вида 
(7.1).
При f(x, y) ³ 0 каждое слагаемое можно рассматривать как объем малого цилиндра с основанием DSi и высотой f (xi, hi), а сумму – как объем некоторого “ступенчатого” тела (геометрическая интерпретация). Способы разбиения области D на элементарные могут быть различны, однако, если максимальный диаметр (диаметр наибольшей элементарной области) стремится к нулю (при этом n ® ¥), то справедлива следующая теорема:
Если функция f(x, y) непрерывна в замкнутой области D, то предел интегральной суммы (7.1) при max di ® 0 существует и не зависит ни от способа разбиения области D на элементарные, ни от выбора точек внутри элементарных областей (теорема существования двойного интеграла). Этот предел называется двойным интегралом от функции f(x, y) по области D и
обозначается так: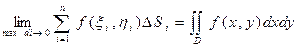 
(7.2).
Область D называется областью интегрирования. Если f(x, y) ³ 0 в области D, то двойной интеграл 
численно равен объему цилиндрического тела, ограниченного сверху поверхностью z = f(x, y), сбоку цилиндрической поверхностью с образующими, параллельными оси Оz (направляющая- граница области D), и снизу областью D плоскости хОу.
Основные свойства двойного интеграла определяются теоремами:
1. Двойной интеграл от суммы функций j(х,у) и f(x, y) по области D равен сумме двойных интегралов по области D от каждой из функций, т.е.
(7.3)
2. Постоянный множитель можно вынести за знак двойного интеграла, т.е. если C = const, то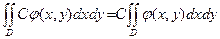 
(7.4).
3. Если область D разбита на две области D1 и D2 без общих внутренних
точек, то 
(7.5).
|
Для вычисления двойного интеграла по правильной области используется разновидность определённого интеграла по плоской области D называемая двукратным интегралом и определяемая выражением:
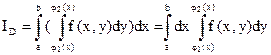(7.6)
В этом выражении сначала вычисляется интеграл по dy («внутренний» интеграл, стоящий в скобках), при этом х считается постоянной. В результате получится непрерывная (доказательство не приводим) функция от х: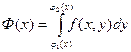 
. Эта функция интегрируется по х в пределах от а до b: 
.
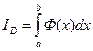Пример: вычислить 
(Область D представляет собой треугольник: а = 0; b = 1; j1(x) = 0 и j2(x) = х2). Вычислим
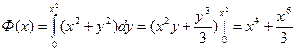и затем 
.
Основные свойства двукратного интеграла:
1. Если правильную в направлении оси Оу(Ох) область D разбить на две области D1 и D2 прямой, параллельной оси Оу(Ох) то двукратный интеграл ID по области D будет равен сумме таких же интегралов по областям D1 и D2, т.е. ID = ID1+ ID2.
Следствие: двукратный интеграл по области D равен сумме двукратных интегралов по частичным областям, т.е. ID = I D1+ I D2+ … +I Dn (области Di выбором границ можно сделать правильными в направлении оси Оу(Ох)).
2. (Оценка двукратного интеграла). Если m и М наименьшее и наибольшее значения функции f(x, y) в области D и S – площадь области D, то справедливо неравенство 
.
3. (Теорема о среднем) Двукратный интеграл от непрерывной функции f(x, y) по области D с площадью S равен произведению полощади S на значение функции в некоторой точке Р области D т.е. 
.
Свойства двукратного интеграла позволяют доказать теорему, открывающую путь к вычислению двойного интеграла: Двойной интеграл от непрерывной функции f(x, y) по области D равен двукратному интегралу от этой функции по области D т.е. 
(7.7)
(Полагаем область D правильная по оси Оу и ограничена линиями у = j1(х), у = j2(х), х =а, х = b).
Пример: Вычислить 
, если область D ограничена линиями у = 1 – х2, у = 2х, х = – 2, х = 0. Построим область D (рис.7.3). Очевидно, она правильная в направлении оси Оу и искомый интеграл равен двукратному интегралу
Отметим, что если область D правильная в направлении оси Ох и ограничена линиями х = y1(у), х = y2(у), у = с, у = d причем y1(у) £ y2(у), то
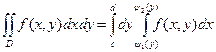(7.8).
Таким образом, двойной интеграл может быть вычислен по формулам (7.7) или (7.8). Пример: Изменить порядок интегрирования в интеграле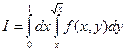 
. Область интегрирования ограничена прямой у = х и параболой 
(рис.7.4) и, очевидно, правильная, т.е. интеграл можно вычислить и по формуле (7.8)
полагая у2 = y1(у), у = y2(у), с = 0, d = 1
откуда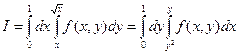 
.
В случае, когда область D не является правильной ни по одной из осей, двойной интеграл по этой области представить в виде двукратного нельзя. Однако, если область D разбить на частичные, правильные в направлении той или иной оси, то двойной интеграл по области D можно представить в виде суммы двойных интегралов по этим областям, а каждое слагаемое – в виде двукратного интеграла по соответствующей частичной области.
