Определенный интеграл.
 Основные определения и теоремы. Пусть на отрезке [a, b] задана непрерывная функция y = f(x) (рис.6.1). Обозначим через m и M ее наименьшее и наибольшее значения на этом отрезке. Разобьем отрезок [a, b] на n произвольных частей точками
Основные определения и теоремы. Пусть на отрезке [a, b] задана непрерывная функция y = f(x) (рис.6.1). Обозначим через m и M ее наименьшее и наибольшее значения на этом отрезке. Разобьем отрезок [a, b] на n произвольных частей точками
|

суммы  (6.1) и
(6.1) и  (6.2), называемые нижней и верхней интегральными суммами.
(6.2), называемые нижней и верхней интегральными суммами.
S n (при f (x) ³ 0)численно равна площади вписанной ступенчатой фигуры АС0N1C1N2…Cn–1NnBA, a ` Sn – площади описанной фигуры AK0C1K1…Kn–1CnBA. Так как mi £ Mi для любого i, то S n £ `Sn (знак равенства соответствует случаю f(x) = сonst). Так как m1 ³ m, m2 ³ m, …, mn ³ m (m –наименьшее значение f(x) на [a, b]), то, S n ³ m(b–a). Так как M1 £ M, M2 £ M,…, Мn £ M (М – наибольшее значение f(x) на [a, b]), то Sn £ M (b – a), т.е. площадь криволинейной трапеции АС0CnВ меньше площади описанного и больше площади вписанного прямоугольников.
Возьмем на каждом из отрезков Dхi произвольную точку xi, найдем соответствующее значение функции f(xi) и составим сумму  , называемую интегральной суммой для функции f(x) на отрезке [a, b]. Очевидно, что mi £ f(xi) £ Mi, miDxi £ f(xi)Dxi < MiDxi и S n £ Sn £ `Sn. (Фигура, площадь которой равна Sn, ограничена ломаной, заключенной между вписанной и описанной ломаными). Sn зависит от способа разбиения отрезка [a, b] на отрезки Dxi и от выбора точек xi внутри Dxi. Обозначим через maxDxi наибольшую из длин этих отрезков и потребуем, чтобы maxDxi ® 0. Число отрезков при этом стремится к бесконечности. Если при любых разбиениях отрезка [a, b] таких, что maxDxi ® 0 и при любом выборе точек xi суммы
, называемую интегральной суммой для функции f(x) на отрезке [a, b]. Очевидно, что mi £ f(xi) £ Mi, miDxi £ f(xi)Dxi < MiDxi и S n £ Sn £ `Sn. (Фигура, площадь которой равна Sn, ограничена ломаной, заключенной между вписанной и описанной ломаными). Sn зависит от способа разбиения отрезка [a, b] на отрезки Dxi и от выбора точек xi внутри Dxi. Обозначим через maxDxi наибольшую из длин этих отрезков и потребуем, чтобы maxDxi ® 0. Число отрезков при этом стремится к бесконечности. Если при любых разбиениях отрезка [a, b] таких, что maxDxi ® 0 и при любом выборе точек xi суммы  стремятся к одном у и тому же пределу, то говорят, что функция f(x) интегрируема на отрезке [ a, b]. Предел этот называют определенным интегралом от функции f(x) на отрезке [a, b]
стремятся к одном у и тому же пределу, то говорят, что функция f(x) интегрируема на отрезке [ a, b]. Предел этот называют определенным интегралом от функции f(x) на отрезке [a, b]
 (6.3).
(6.3).
Числа а и b называют нижним, и верхним пределами интеграла, отрезок [a, b] – отрезком интегрирования, х – переменной интегрирования.
Приведем теорему существования определенного интеграла: Если функция f(x) непрерывна на [a, b], то предел интегральной суммы существует ине зависит от способа разбиения отрезка [a, b] на элементарные отрезки Dxi и от выбораточек xi. Если f(x) ³ 0 на [a, b], то определенный интеграл  геометрически представляет собой площадь криволинейной трапеции, ограниченной линиями y = f(x), х =а, х = b, у = 0.
геометрически представляет собой площадь криволинейной трапеции, ограниченной линиями y = f(x), х =а, х = b, у = 0.
Приведем основные свойства определенного интеграла:

 , где с = const.
, где с = const.
6). Если m £ f(x) £ M на [a, b], то 
Непосредственное вычисление определенных интегралов как пределов интегральных сумм связано с большими трудностями и требует громоздких вычислений. Рассмотрим метод, упрощающий решение проблемы и использующий связь между интегрированием и дифференцированием.
Формула Ньютона – Лейбница. Пусть в определенном интеграле нижний предел а фиксирован, а верхний b меняется. Вместе с ним меняется и значение функции, т.е. интеграл есть функция верхнего предела. Для работы в привычных обозначениях верхний предел обозначим через х, а чтобы не смешивать его с переменной интегрирования, обозначим ее через t и получим Ф  . Если f(t) – неотрицательная функция, то величина Ф(х) численно равна площади криволинейной трапеции аАХх (рис.6.2.), меняющейся при значении х. Производная Ф`(х) по х определится теоремой: если f(x) – непрерывная функция и Ф
. Если f(t) – неотрицательная функция, то величина Ф(х) численно равна площади криволинейной трапеции аАХх (рис.6.2.), меняющейся при значении х. Производная Ф`(х) по х определится теоремой: если f(x) – непрерывная функция и Ф  , то имеет место равенство Ф`(х) = f(x), т.е. производная от определенного интеграла по верхнему пределу равна подинтегральной функции, в которую вместо переменной интегрирования подставлено значение верхнего предела.
, то имеет место равенство Ф`(х) = f(x), т.е. производная от определенного интеграла по верхнему пределу равна подинтегральной функции, в которую вместо переменной интегрирования подставлено значение верхнего предела.
(Из этой теоремы следует, в частности, что всякая непрерывная функция имеет первообразную).
Возможности вычисления определенного интеграла открывает следующая теорема: Если F(x) есть какая – либо первообразная непрерывной функции f(x ), то справедлива формула
 (6.4).
(6.4).
Это и есть «знаменитая» формула Ньютона – Лейбница, благодаря которой математика получила общий метод решения большого числа различных задач, связанных с необходимостью вычисления определенного интеграла. Пример: 
При вычислении определенных интегралов по формуле Ньютона – Лейбница может применяться весь арсенал известных приемов нахождения первообразной, например:
1. Метод замены переменной: Если дан интеграл  , где функция f(x) непрерывна на [a, b] и вводится новая переменная по формуле х = j(t), причем j(a) = а, j(b) = b, j(t) и j`(t) непрерывны на [a, b] и f[j(t)] определенаи непрерывна на [a, b], то
, где функция f(x) непрерывна на [a, b] и вводится новая переменная по формуле х = j(t), причем j(a) = а, j(b) = b, j(t) и j`(t) непрерывны на [a, b] и f[j(t)] определенаи непрерывна на [a, b], то  (6.5).
(6.5).
При вычислении определенного интеграла по формуле (6.5) мы не возвращаемся к старой переменной, а находим новые пределы интегрирования a и b. Пример:  [примем х = r cost; dx = –r sint dt;
[примем х = r cost; dx = –r sint dt;
x = 0 при t = p/2 и x = r при t = 0] = 
(Геометрически это площадь ¼ круга радиуса r).
2. Интегрирование по частям. Пусть u и v дифференцируемые функции от х. Тогда d(uv) = udv + vdu. Интегрируя обе части равенства в пределах от а до b получим  , откуда
, откуда  (6.6).
(6.6).
Пример: 
Приведем еще два соотношения, упрощающие вычисления в ряде случаев. Если f(x) – нечетная функция, то  (6.7).
(6.7).
и, если f(x) четная функция, то  (6.7 ‘).
(6.7 ‘).
Приложения определенного интеграла к задачам практики.
 1. Площадь плоской фигуры. Площадь криволинейной трапеции, ограниченной кривой y = f(x), прямыми х = а и х = b и отрезком [a, b], (рис.6.3) вычисляется по формуле
1. Площадь плоской фигуры. Площадь криволинейной трапеции, ограниченной кривой y = f(x), прямыми х = а и х = b и отрезком [a, b], (рис.6.3) вычисляется по формуле  (6.8).
(6.8).
Легко видеть, что площадь фигуры, ограниченной кривыми y = f1(x) и y = f2(x); 0 £ f 2(х) £ f1(x) и прямыми х = а и х = b определится соотношением
|
 (6.9).
(6.9).
В полярных координатах площадь криволинейного сектора, ограниченная кривой r = r(j) и двумя полярными радиусами j = a и j = b(a < b) определится выражением  (6.10),
(6.10),
а площадь фигуры, ограниченной кривыми r1(j), r2(j), r2(j) £ r1(j) и радиусами j = a и j = b выражением  (6.10`).
(6.10`).
|
 2. Длина дуги плоской кривой. Пусть на плоскости дана кривая y = f(x). Найдем длину дуги АВ этой кривой между прямыми х = а и х = b (рис.6.4.). Возьмем на дуге точки А, М1, …, Мi, …, В с абсциссами х0 =а, х1, …xi, …,xn= b и проведем хорды А М1, М1М2, …, Мi–1Mi, …, Mn–1 B, длины которых обозначим через DSi. Получим ломаную АМ1М2 …Мi …В, вписанную в дугу АВ. Длина ломаной равна
2. Длина дуги плоской кривой. Пусть на плоскости дана кривая y = f(x). Найдем длину дуги АВ этой кривой между прямыми х = а и х = b (рис.6.4.). Возьмем на дуге точки А, М1, …, Мi, …, В с абсциссами х0 =а, х1, …xi, …,xn= b и проведем хорды А М1, М1М2, …, Мi–1Mi, …, Mn–1 B, длины которых обозначим через DSi. Получим ломаную АМ1М2 …Мi …В, вписанную в дугу АВ. Длина ломаной равна  . Длиной S дуги АВ называется предел, к которому стремится длина вписанной ломаной, когда длина ее наибольшего звена стремится к нулю:
. Длиной S дуги АВ называется предел, к которому стремится длина вписанной ломаной, когда длина ее наибольшего звена стремится к нулю:  .
.Если на отрезке [a, b] функции f(x) и f `(x) непрерывны (кривая – гладкая), то этот предел существует и равен  (6.11).
(6.11).
Если гладкая кривая задана в полярных координатах уравнением r = r(j) (a £ j £b), длина дуги равна  (6.12).
(6.12).
3. Вычисление объема тела по параллельным сечениям. Если площадь сечения тела плоскостью, перпендикулярной оси Ох, может быть выражена как функция от х, т.е. в виде S = S(x), то объем части тела, заключенной между плоскостями х = а и x = b, определится формулой  (6.13)
(6.13)
4. Объем тела вращения. Если криволинейная трапеция, ограниченная кривой y = f(x) и прямыми х = а и х = b, вращается вокруг оси Ох, то объем тела вращения определится соотношением  (6.14).
(6.14).
Если вокруг оси Ох вращается фигура, образованная кривыми y = f1(x) и y = f2(x) (0 £ f1(x) £ f2(x)) и прямыми х = а и х = b, то объем тела вращения
 (6.15).
(6.15).
5. Поверхность тела вращения. Если дуга гладкой кривой y = f(x) (а £ х £ b) вращается вокруг оси Ох, то площадь поверхности вращения вычисляется по формуле  (6.16).
(6.16).
6. Работа и давление. Работа переменной силы F = f(x), действующей по оси Ох на отрезке [a, b] вычисляется по формуле  (6.17)
(6.17)

|
Пример: Какое давление испытывает прямоугольная пластина длиной а и шириной b (a > b), если она наклонена к поверхности жидкости под углом a и ее большая сторона находится на глубине h (рис.6.5)?
Площадь выделенной на глубине х элементарной полоски равна  . Следовательно,
. Следовательно,  (r – плотность жидкости). Отсюда находим
(r – плотность жидкости). Отсюда находим  .
.
Несобственные интегралы.
Интеграл с бесконечными пределами. Рассмотрим интеграл  . При переменном b он является непрерывной функцией b. Предел этой функции при b ® ¥ обозначают
. При переменном b он является непрерывной функцией b. Предел этой функции при b ® ¥ обозначают  (6.18)
(6.18)
и называют несобственным интегралом от функции f(x) на интервале [a, ¥). Если этот предел существует и конечен- интеграл называют сходящимся; если же предел не существует или равен бесконечности – расходящимся. Геометрический смысл в случае f(x) ³ 0 – площадь неограниченной области, заключенной между линиями y = f(x), х = а и у = 0 (ось Ох).
Пример: (рис.6.6) 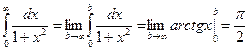 .
.
 |
Аналогично определяются интегралы:  (6.18`)
(6.18`)
и  (6.18``).
(6.18``).
Бывает достаточно установить, сходится или расходится данный интеграл и оценить его значение. Это позволяют сделать следующие теоремы:
1. Если для всех х ³ а выполняется неравенство о £ f(x) £ j(х) и если  сходится, то сходится и
сходится, то сходится и  , причем
, причем  £
£  .
.
2. Если для всех х ³ а выполняется неравенство f(x) ³ j(х) ³ 0, причем  расходится, то расходится и
расходится, то расходится и  .
.
3. Если интеграл  сходится, то сходится и
сходится, то сходится и  . В последнем случае говорят, что интеграл абсолютно сходящийся.
. В последнем случае говорят, что интеграл абсолютно сходящийся.
Пример: исследовать сходимость  . Подинтегральная функция знакопеременная. Рассмотрим
. Подинтегральная функция знакопеременная. Рассмотрим  . Очевидно, что
. Очевидно, что  ;
;  . Исходный интеграл сходится абсолютно.
. Исходный интеграл сходится абсолютно.
Интеграл от неограниченной функции. Пусть функция y = f(x) определена и непрерывна при а £ х < с, а в точке с испытывает бесконечный разрыв. Интеграл  (6.19)
(6.19)
называют несобственным интегралом от неограниченной функции.
Если этот предел существует и конечен – интеграл сходящийся, если нет – расходящийся. Аналогично определяются интегралы
 (6.19`)
(6.19`)
(при а < x £ c и  ), и, если функция имеет бесконечный разрыв в точке с внутри отрезка [a, b],
), и, если функция имеет бесконечный разрыв в точке с внутри отрезка [a, b], 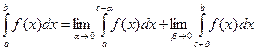 (6.19``).
(6.19``).
Несобственный интеграл (6.19``) называют сходящимся, если существуют оба предела в правой части равенства, и расходящимся, если не существует хотя бы один из них. Для решения вопроса о сходимости несобственных интегралов от разрывных функций и оценки их значений полезны следующие теоремы: 1. Если на отрезке [a, с] функции f(x) и j(х) разрывны в точке с, причем во всех точках этого отрезка j(х) ³ f(x) ³ 0 и  сходится, то
сходится, то  также сходится; 2. Если на отрезке [a, с] функции f(x) и j(х) разрывны в точке с, причем во всех точках этого отрезка f(x) ³ j(х) ³ 0 и
также сходится; 2. Если на отрезке [a, с] функции f(x) и j(х) разрывны в точке с, причем во всех точках этого отрезка f(x) ³ j(х) ³ 0 и  расходится то и
расходится то и  расходится; 3. Если функция f(x), знакопеременная на отрезке [a, с], разрывная только в точке с и интеграл
расходится; 3. Если функция f(x), знакопеременная на отрезке [a, с], разрывная только в точке с и интеграл  сходится, то сходится (абсолютно) и
сходится, то сходится (абсолютно) и  .
.
Пример: Сходится ли  ? Подинтегральная функция разрывна при х = 0. В указанном интервале
? Подинтегральная функция разрывна при х = 0. В указанном интервале  . Несобственный интеграл
. Несобственный интеграл 
сходится, и, соответственно, сходится исходный интеграл.
Тесты
3.10.  ;
; 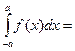
1) 0; 2)  ; 3)
; 3)  .
.
3.11.  ;
; 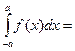
1) 0; 2)  ; 3)
; 3)  .
.
3.12. 
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
3.13. 
1)  ; 2)
; 2) 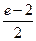 ; 3)
; 3)  ; 4)
; 4) 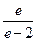 .
.
3.14. 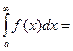
1)  ; 2)
; 2) 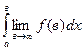 ; 3)
; 3) 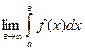 .
.
3.15. Сходится ли  и, если да, то равен:
и, если да, то равен:
1) 0; 2)  ; 3) 1.
; 3) 1.
3.16. Сходится ли  и, если да, то равен:
и, если да, то равен:
1) 0; 2) –3; 3) 2p.
3.17. 
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
3.18. 
1) Сходится; 2) Расходится.
3.19. Площадь фигуры, ограниченной линиями  и
и  , равна (кв.ед):
, равна (кв.ед):
1) 7; 2) –3,5; 3) 4,5; 4) 6,2.
3.20. Объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями  и
и  составляет (куб.ед.):
составляет (куб.ед.):
1) 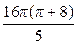 ; 3)
; 3) 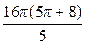 ;
;
2)  ; 4)
; 4)  .
.






