Вычисления с помощью двойного интеграла

1. Объем. Напомним, что объем V тела, ограниченного сверху поверхностью z = f(x, y)(f(x, y) ³ 0), снизу – плоскостью z = 0, а сбоку – цилиндрической поверхностью, направляющей для которой служит граница области D, а образующая параллельна оси Oz, определится соотношением

(7.9).

1.1. Если тело ограничено сверху поверхностью z = f₁(x, y) ³ 0, снизу – поверхностью z = f₂(x, y) ³ 0, причем проекцией обеих поверхностей на плоскость хОу является область D, то объем V этого тела равен разности объемов двух цилиндрических тел: оба имеют нижним основанием область D, а верхним – поверхности z = f₁(x, y) ³ 0 для первого и z = f₂(x, y) ³ 0 для второго,

(7.10)

Формула (7.10) верна и тогда, когда f₁(x, y) и f₂(x, y) – любые непрерывные функции, удовлетворяющие неравенству f₁(x, y) ³ f₂(x, y).

1.2. Если в области D функция f(x, y) меняет знак, то следует разбить область на две части: D₁, где f(x, y) ³ 0 и D₂, где f(x, y) £ 0. Если области D₁ и D₂ таковы, что двойные интегралы по ним существуют, то первый будет равен объему тела, лежащего выше плоскости хОу, а второй – объему тела, лежащего ниже плоскости хОу.

2. Площадь плоской области. Площадь области D в плоскости хОу численно равна объему рассмотренного цилиндра, ограниченного сверху в нашем случае поверхностью z = f(x, y) = 1, т.е. или, если область D правильная (7.11).

3. Площадь поверхности, заданной уравнением z = f(x, y) и ограниченной некоторой замкнутой линией С. Проекцию этой линии на плоскость хОу обозначим через L, а область, ограниченную линией L, обозначим через D. Если функция f(x, y) непрерывна и имеет непрерывные частные производные в этой замкнутой области, то искомая площадь поверхности определится выражением 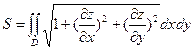(7.12).

С помощью двойного интеграла можно решить и целый ряд “физических” задач: вычисление массы плоских пластин с известной поверхностной плотностью r = f(x, y), момента инерции плоской фигуры и т.д.

Тройной интеграл. Пусть в декартовых трехмерных координатах задана «объемная» область V, ограниченная замкнутой поверхностью S и пусть в каждой точке этой области, включая границу, определена непрерывная функция f(x, y, z). Разобьем область V произвольным образом на малые области (объемы) DV_i, выберем в каждой произвольную точку Р_i(x_i, y_i, z_i) и составим интегральную сумму вида . Устремляя максимальный диаметр maxd_i (и, соответственно, объем DV_i) к нулю (maxd_i ® 0) перейдем к пределу интегральной суммы. При условиях, перечисленных выше, этот предел существует и называется тройным интегралом:

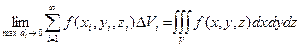(7.13).

где dxdydz = dV элемент объема в декартовых координатах. Если f(x, y, z) ³ 0 описывает плотность распределения вещества в объеме V, то (7.13) даст массу этого вещества.

Если: 1. Всякая прямая, параллельная оси Оz и проходящая через внутреннюю точку области V, пересекает поверхность S в двух точках;

2. Область V проектируется на плоскость хОу в правильную двумерную область D; 3. всякая часть области V, отсеченная плоскостью, параллельной одной из координатных обладает свойствами 1. и 2. – область V называют правильной.

Введем понятие трехкратного интеграла I_v по области V от функции f(x, y, z) определенной и непрерывной в этой области. Пусть z = y₁(x,y) и z = y₂(x,y) уравнения поверхностей, ограничивающиx область V снизу и сверху (вместе они описывают замкнутую поверхность S), а область D – проекция V на плоскость xОу – ограничена линиями у = j₁(х), у = j₂(х), х = а, x = b.

Трехкратный интеграл I_v определяется выражением:

(7.14)

При интегрировании по z переменные х и у считаем постоянными. После интегрирования по z и подстановки пределов получаем двукратный интеграл, рассмотренный в предыдущем разделе. Трехкратный интеграл обладает свойствами, аналогичными свойствам двукратного: 1. Если область V разбить на две областии V₁ и V₂ плоскостью, параллельной одной из координатных, то трехкратный интеграл по области V равен сумме трехкратных интегралов по областям V₁ и V₂. (При любом разбиении области V на конечное число V₁, V₂, …,V_n плоскостями, параллельными координатным, справедливо равенство: I_V = I_V1+ I _V2+ … +I_Vn). 2. Если m и М – наименьшее и наибольшее значения функции f(x, y, z) в области V, то справедливо неравенство mV £ I_v £ MV, где V – объем области, I_v – трехкратный интеграл от f(x, y, z) по области V.

3. (теорема о среднем) Трехкратный интеграл I_v от непрерывной функции f(x, y, z) по области V равен произведению ее объема V на значение

функции в некоторой точке Р области V:

 

Приведенные свойства трехкратного интеграла позволяют доказать теорему о вычислении тройного интеграла:

Тройной интеграл от функции f(x, y, z) по правильной области V равен трехкратному интегралу по этой же области:

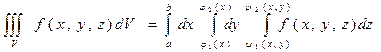(7.15)

 

(Как и в случае двукратного интеграла, можно изменить порядок интегрирования, если это позволяет сделать форма области V. Можно с этой целью разбить область V на части).

Если подинтегральная функция f(x, y, z) = 1, то тройной интеграл по области V дает значение ее объема (7.15`).

Пример: 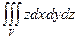, если область V определяется неравенствами: 0 £ х £ ½, х £ у £ 2х, 0 £ z £ 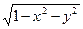(т.е. а = 0, b = ½, j₁(x) = x, j₂(x) = 2x, y₁(x,y) = 0, y₂(x,y) = 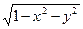, область V представляет собой часть сферы единичного радиуса с центром в начале координат, ограниченную снизу плоскостью хОу(z = 0), а «с боков» плоскостями у = х и у = 2х).

 

 

 

Нередко вычисление тройных интегралов значительно упрощается при переходе к цилиндрическим или сферическим пространственным координатам.

В цилиндрических координатах положение точки Р определяется тремя числами r, j, z, где r и j – полярные координаты проекции точки Р на плоскость хОу, а z – аппликата точки Р. Пространственную область V разбивают на элементарные координатными поверхностями j = j_i, r = r_j, z = z_k. Элементарный объем dV примет вид: dV = rdrdjdz, а тройной интеграл: 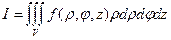, пределы интегрирования в соответствующем трехкратном интеграле определятся формой области V. Зная формулы связи:

х = rcosj, y = rsinj, z = z несложно перейти от декартовых координат к цилиндрическим: .

Пример: , если область V ограничена цилиндром х² + у² = 2х и плоскостями у = 0, z = 0, z = a. Перейдем к цилиндрическим координатам. Уравнение цилиндра примет вид r²cos²j + r²sin²j = 2rcosj => r²(cos²j + sin²j) = 2rcosj => r = 2 cosj. Область V определяется неравенствами: 0 £ r £ 2cosj, 0 £ j £ p/2, 0 £ z £ а и

В сферических координатах положение точки Р определяется числами j, r, q, где r – расстояние точки от начала координат, q – угол между r и осью Оz и j – угол между проекцией r на плоскость хОу и осью Ох (отсчитывается, как обычно, от оси Ох против часовой стрелки). Декартовы координаты связаны со сферическими так: х = rsinqcosj, у = rsinqsinj, z = rcosq (0 £ r £ ¥, 0 £ j £ 2p, 0 £ q £ p). Элемент объема в сферических координатах dV = r²sinqdrdjdq. В итоге можем перейти от тройного интеграла в декартовых координатах к тройному интегралу в сферических координатах.

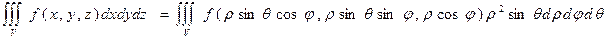
Пример: , если область V – верхняя половина шара x² + y² + z² £ r². Перейдя к сферическим координатам получим: 0 £ r £ r, 0 £ j £ 2p, 0 £ q £ p/2, x² + y² = r²sin²qcos²j + r²sin²qsin²j = r²sin²q и

 

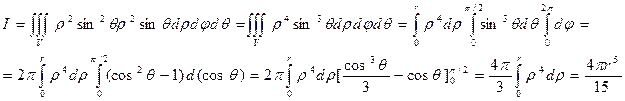
Криволинейный интеграл.