Задания по начертательной геометрии

Для решения различными способами

В графической среде AutoCAD

 

 

Варианты заданий 1 и 8 приводятся с решениями и описанием методики решения в AutoCAD. Для комфортности решения предлагается использовать поэтапный выбор цветов.

В вариантах 4, 7, 8, 9 предлагается самостоятельно определить, как конкретно сделать проверку.

При выполнении заданий предлагается также использовать дополнительные варианты решений или свою оригинальную методику решения в среде AutoCAD. При решении задач в группе организовывается соревнование, и такие предложения студентов оцениваются преподавателем особенно высоко. Рекомендуется после выполнения заданий устраивать обсуждения их решений в группе.

 

Вариант 1

Дано: основание пирамиды АВС (А₁В₁С₁; А₂В₂С₂). А₁(67;142); А₂(67;188); В₁(92;100); В₂(92; 235); С₁(130;115); С₂(130; 202).

Построить: пирамиду с ребром CS, перпендикулярным АВС, длиной 55 мм.

1. Решение выполнить:

– с использованием теоремы о проекции прямого угла и метода вращения вокруг проецирующей прямой;

– с использованием метода замены плоскостей проекций.

2. Проверить правильность решения задачи путем сравнения результатов решения с применением команды «Расстояние».

3. Сделать сравнение способов решения и вывод.

4. Какой еще известный вам метод решения задач начертательной геометрии можно применить при решении данной задачи?

 

Решение

Результат построения основания пирамиды приведен на рис. 47. Построение выполняется с использованием команды «Отрезок» (Line). Координаты проекций точек вводятся с клавиатуры.

Выполняется 1-й способ для построения направления ребра пирамиды CS. Для этого в плоскости вводятся горизонталь h и фронталь f. При этом горизонтали присваивается фиолетовый цвет, а фронтали – синий (рис. 48). Используется команда «Отрезок», режим «ОРТО» и постоянный режим объектной привязки «Пересечение». При всех дальнейших построениях режим «Пересечение» остается включенным, и применение его больше не упоминается.

Для построения проекции перпендикуляра n к плоскости АВС, восстановленным из точки С, сначала выполняются отрезки, перпендикулярные f₂ и h₁, в произвольном месте (рис. 49) с использованием режима объектной привязки «Нормаль» и последующим переносом и использованием команды «Переместить» (Move) (рис. 50).

На перпендикуляре n выбирается произвольная точка D (D₁, D₂) с использованием режима объектной привязки «Ближайшая», режима «ОРТО» и команды «Отрезок» (рис. 51).

Затем выполняется построение натуральной величины отрезка CD (рис. 52) методом вращения вокруг проецирующей прямой i (i₁, i₂) с использованием команд «Круг», «Отрезок» и «Разорвать» режима объектной привязки «Пересечение» и режима «ОРТО».

Для построения вершины пирамиды натуральная величина ребра 55 откладывается на направлении натуральной величины (С₂, D₂) с использованием команд «Круг», «Удлинить» (Обрезать» в случае, когда С₂, D₂ больше 55) и «Разорвать» (рис. 53). Результат построения пирамиды SABC данным способом показан на рис. 54.

 

 

Рис. 47. Результат построения основания пирамиды

 

Рис. 48. Построение фронтали и горизонтали основания

 

 

 

Рис. 49. Построение проекции перпендикуляра n

 

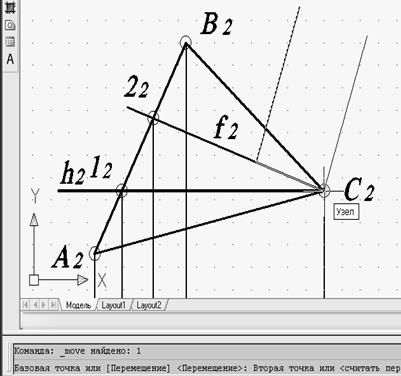
Рис. 50. Перемещение проекции перпендикуляра n

 

 

 

Рис. 51. Выбор произвольной точки D

 

Рис. 52. Построение натуральной величины отрезка CD

 

 

 

Рис. 53. Построение вершины пирамиды

 

Рис. 54. Результат построения пирамиды первым способом

 

 

 

Рис. 55. Замена плоскости проекций

с использованием фронтали

При использовании способа замены плоскостей проекций в данном примере замещается горизонтальная плоскость проекций П₁ на новую плоскость проекций П₄. Для этого в плоскости АВС вводится фронталь f (рис. 55), а новая ось X₁₄ и новые линии связи вводятся перпендикулярно фронтальной проекции фронтали f₂. При этом используется режим объектной привязки «Нормаль».

Для построения проекций основания пирамиды и ее ребра от точек пересечения линий связи и оси X₁₄ глубины точек А, В и С откладываются с использованием команд «Копировать», «Круг» и «Удлинить» («Обрезать»). Команда «Круг» выполняется с применением режима объектной привязки «Конточка» (рис. 56). Глубины точек рекомендуется выделить цветом, отличным от других цветов, используемых в данном примере.

 

 

Рис. 56. Построение проекции точки С₄

 

 

Выполнение команды «Удлинить» при указании удлиняемого объекта для построения проекции точки С₄ показан на рис. 57. Построение проекций точек А₄ и В₄ выполняется аналогично. Результат построения проекции основания А₄С₄В₄ приведен на рис. 58.

 

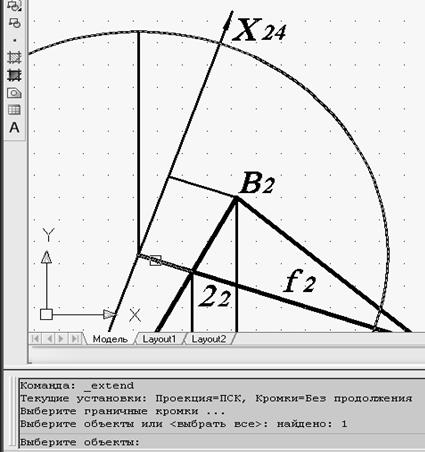
Рис. 57. Указание удлиняемого объекта

при выполнении команды «Удлинить»

для построения проекции точки С₄

 

 

 

Рис. 58. Результат построения проекции основания А₄С₄В₄

Построение проекции ребра S₄С₄ выполняется в 4 этапа. Сначала строится из произвольной точки перпендикуляр к проекции основания пирамиды А₄С₄В₄ (рис. 59). Перпендикуляр переносится с использованием команды «Переместить» в проекцию точки С₄. Затем строится круг с использованием команды «Круг» с центром в С₄ радиусом 55 (рис. 60), до которого перпендикуляр либо удлиняется («Удлинить»), либо обрезается («Обрезать»). Наконец, круг удаляется командой «Стереть». Результат построения проекции ребра S₄С₄ приводится на рис. 61.

 

 

Рис. 59. Построение перпендикуляра

к проекции основания пирамиды

 

 

Затем производится построение проекции вершины S₂. Проекция ребра S₄С₄ является натуральной величиной, а значит, линией уровня. Поэтому на фронтальной плоскости проекций она должна быть параллельна оси X₁₄. Построение ее начинается копированием оси X₁₄ в С₂ (рис. 61, отрезок а). Линия связи строится перпендикулярно оси X₁₄ до пересечения с отрезком а (рис. 61, S₂). Результат построения проекции ребра S₂С₂ показан на рис. 62.

 

Рис. 60. Указание удлиняемого перпендикуляра

при построении проекции ребра пирамиды S₄С₄

 

 

 

Рис. 61. Копирование оси и построения проекции S₂

 

Рис. 62. Результат построения проекции ребра S₂С₂

 

 

 

Рис. 63. Построение проекции вершины пирамиды S₁

 

Рис. 64. Результат построения проекции ребра S₁С₁

 

 

 

Рис. 65. Результат построения пирамиды

вторым способом

 

 

Для построения проекции вершины пирамиды S₁ проводится линия связи от S₂ с использованием режима «ОРТО» (рис. 63, отрезок b), координата S₄ копируется в точку пересечения оси X₁₂ и линии связи (рис. 63, отрезок c). Построение проекции точки S₁ выполняется аналогично построению проекций точек С₄, В₄, А₄. Результат построения проекции ребра S₁С₁ показан на рис. 64. На рис. 65 показан результат построения всех проекций пирамиды вторым способом с использованием команд «Отрезок» и «Тип линии».

 

 

Рис. 66. Измерение проекции ребра,

построенного первым способом

 

 

 

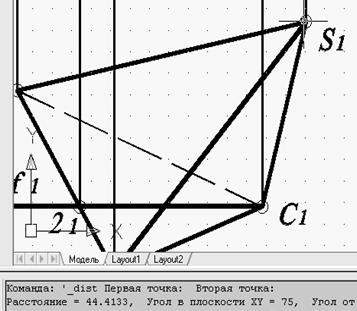
Рис. 67. Измерение проекции ребра,

построенного вторым способом

Сравнение результатов решения задачи обоими способами выполняется измерением проекции ребра S₁С₁ с использованием команды «Расстояние» (рис. 66, 67).

 

Вариант 2

Дано: основание пирамиды АВС (А₁В₁С₁; А₂В₂С₂). А₁(67;142); А₂(67;188); В₁(92;100); В₂(92; 235); С₁(130;115); С₂(130; 202).

Построить: пирамиду с ребром АS, перпендикулярным АВС, длиной 50.

1. Решение выполнить:

– с использованием теоремы о проекции прямого угла и метода прямоугольного треугольника;

– с использованием метода замены плоскостей проекций.

2. Проверить правильность решения задачи путем сравнения результатов решения с применением команды «Площадь».

3. Сравнить способы решения задачи и сделать вывод.

 

Вариант 3

Дано: основание пирамиды АВС (А₁В₁С₁; А₂В₂С₂). А₁(67;142); А₂(67;188); В₁(92;100); В₂(92; 235); С₁(130;115); С₂(130; 202).

Построить: пирамиду с ребром ВS, перпендикулярным АВС, длиной 60.

1. Решение выполнить:

– с использованием теоремы о проекции прямого угла и метода прямоугольного треугольника;

– с использованием метода замены плоскостей проекций.

2. Проверить правильность решения задачи путем сравнения результатов решения с применением команды «Копировать».

3. Сравнить способы решения задачи и сделать вывод.

 

Вариант 4

Дано: плоскость АВС (А₁В₁С₁; А₂В₂С₂). А₁(67;142); А₂(67;188); В₁(92;100); В₂(92; 235); С₁(130;115); С₂(130; 202).

Построить: натуральную величину плоскости АВС.

1. Решение выполнить:

– с использованием метода замены плоскостей проекций;

– с использованием метода вращения вокруг проецирующей прямой.

2. Проверить правильность решения задачи путем сравнения результатов решения любыми двумя способами.

3. Сравнить способы решения задачи и сделать вывод.

Вариант 5

Дано: плоскость АВС (А₁В₁С₁; А₂В₂С₂). А₁(44;106); А₂(44;206); В₁(90;146); В₂(90;230); С₁(109;124); С₂(109;196). Точка М(М₁; М₂). М₁(74;98); М₂(74;238).

Построить: точку N, симметричную точке М.

1. Решение выполнить:

– с использованием теоремы о проекции прямого угла в слое 1;

– с использованием метода замены плоскостей проекций в слое 2.

2. Проверить правильность решения задачи путем сравнения результатов решения с использованием команды «Слой».

3. Сравнить способы решения задачи и сделать вывод.

 

 

Рис. 68. Заданная пирамида (вариант 6)

 

 

Вариант 6

Дано: пирамида (рис. 68) SABC (S₁А₁ В₁С₁; S₂А₂ В₂С₂) и плоскость Δ (m÷÷n). m (m₁; m₂). n (n₁; n₂). 1 и 3 Î m. 2 и 4 Î n. S₁(176;97); S₂(176;246); A₁(74;139); A₂(74;175); B₁(103;95); B₂(103;160); C₁(129;127); C₂(129;147); 1₁(103;145); 1₂(103;242); 2₁(103;109); 2₂(103;202); 3₁(165;125); 3₂(165;198); 4₁(165;89); 4₂(165;158).

Построить: сечение пирамиды SABC плоскостью Δ.

1. Решение выполнить:

– с использованием горизонтали плоскости Δ в слое 1;

– с использованием фронтали плоскости Δ в слое 2.

2. Проверить правильность решения задачи путем сравнения результатов решения с использованием команды «Слой».

3. Сравнить способы решения задачи и сделать вывод.

 

 

Рис. 69. Заданная пирамида (вариант 7)

 

 

Вариант 7

Дано: пирамида (рис. 69) SABC (S₁А₁ В₁С₁; S₂ А₂ В₂С₂). S₁(176;97); S₂(176;246); A₁(74;139); A₂(74;175); B₁(103;95); B₂(103;160); C₁(129;127); C₂(129;147).

Построить: натуральные величины ребер пирамиды SABC.

1. Решение выполнить:

– с использованием метода замены плоскостей проекций;

– с использованием метода вращения вокруг проецирующей прямой;

– с использованием метода прямоугольного треугольника.

2. Проверить правильность решения задачи наиболее возможным количеством способов.

3. Сравнить способы решения задачи и сделать вывод.

 

Вариант 8

Дано: плоскость ABC (А₁В₁С₁; А₂В₂С₂). A₁(67;142); A₂(67;188); B₁(92;100); B₂(92;235); C₁(130;115); C₂(130;202).

Построить: натуральную величину плоскости ABC.

1. Решение выполнить:

– с использованием метода вращения вокруг прямой уровня (фронтали);

– с использованием метода вращения вокруг прямой уровня (горизонтали).

2. Выбрать и обосновать наиболее удобный и полезный способ последовательности построений.

3. Проверить правильность решения задачи наиболее удобным способом.

4. Сравнить результаты решения задачи заданными методами и сделать вывод.

 

Решение

Прежде всего, следует определить, в каком порядке решать задачу обоими способами. Рассмотрим возможные варианты.

Можно решать поочередно задачу 1-м способом в одном файле, затем 2-м способом в другом.

Можно решать в той же очередности, но в одном файле и в разных слоях, чтобы скопировать один результат и наложить на другой для сравнения. Однако следует учесть тот факт, что результаты решения без поворота одного из них нельзя будет наложить для их сравнения. В этом случае удобно измерить площади построенных натуральных величин и сравнить.

И, наконец, предлагается третий вариант порядка решения: выполнять построения в одном файле параллельно таким образом, чтобы каждый этап решения 1-м способом сразу повторялся для решения 2-м способом. Преимущества этого порядка построений очевидны.

Во-первых, легче использовать логическое разнообразие цветов. Во-вторых, повторение решения удобно для закрепления материала, кроме того, повторение идентичных этапов помогает лучше сосредоточиться, что способствует снижению вероятности ошибочных построений и в конечном итоге ускорению решения обоими способами. Помимо этого, постоянное переключение с одного способа на другой и сравнение идентичности построений способствует развитию внимательности, памяти, логического мышления и умения анализировать.

Начальные построения выполняются в одном файле с использованием команды «Отрезок» и клавиатуры. Затем с использованием команд «Цвет» и «Отрезок», режима «ОРТО» и постоянного режима объектной привязки «Пересечение» вводится для решения 1-м способом в плоскости фронталь f (рис. 70), а для решении 2-м способом – горизонталь h (рис. 71).

Выбирается точка В для вращения вокруг линий уровня. Для этого первым способом через проекцию точки В₂ строится с использованием режима объектной привязки «Нормаль» проекция фронтально проецирующей плоскости Δ₂ перпендикулярно f₂ (рис. 72). Аналогично для решения 2-м способом через проекцию точки В₁ строится с использованием режима объектной привязки «Нормаль» проекция горизонтально проецирующей плоскости ψ₁ перпендикулярно h₁ (рис. 73). Для обоих способов определяются центры вращения – точка О (рис. 72) и точка Р (рис. 73), и проекции радиусов вращения – О₁В₁ и О₂В₂, Р₁В₁ и Р₂В₂.

 

 

Рис. 70. Ввод фронтали в плоскости

Для определения натуральных величин радиусов вращения используется метод прямоугольного треугольника. При построении 1-м способом копируется разность глубин точки В и фронтали f (отрезок В₁L, рис. 72) в проекцию центра вращения О₂. Затем на проекции фронтали f₂ откладывается отрезок В₁L (О₂R, рис. 72) с использованием команды «Круг» и режима объектной привязки «Конточка». Такое построение описано в решении задачи вариантом 1. При решении 2-м способом аналогично копируется разность высот радиуса вращения В₂М и откладывается на проекции горизонтали h₁ (отрезок P₁N, рис. 73). Для обоих способов выполняются построения натуральных величин радиусов вращения (В₂R, рис. 72) и (В₁N, рис. 73).

Затем для решения 1-м способом натуральная величина радиуса вращения откладывается от проекции центра вращения О₂ на проекции плоскости Δ₂ с использование команд «Копировать», «Круг» и режима объектной привязки «Конточка» (О₂В’₂, рис. 74). Для решения 2-м способом аналогично откладывается натуральная величина радиуса вращения от проекции центра вращения Р₁ на проекции плоскости ψ₁ (Р₁В’₁, рис. 75).

 

 

Рис. 71. Ввод горизонтали в плоскости

 

Рис. 72. Построение проекции

фронтально проецирующей плоскости Δ₂

 

 

 

Рис. 73. Построение проекции

горизонтально проецирующей плоскости ψ₁

 

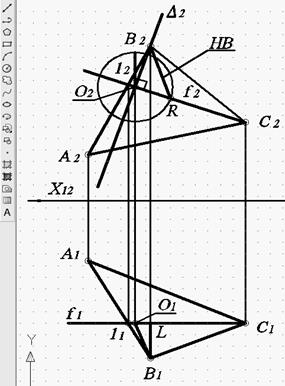
Рис. 74. Построение натуральной величины

радиуса вращения В₂R

 

 

 

Рис. 75. Построение натуральной величины

радиуса вращения В₁N

 

Рис. 76. Построение натуральной величины

радиуса вращения О₂В’₂

 

 

 

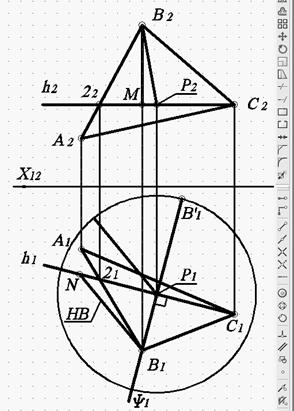
Рис. 77. Построение натуральной величины

радиуса вращения Р₁В’₁

 

Рис. 78. Построение проекции плоскости Δ’₂

 

 

 

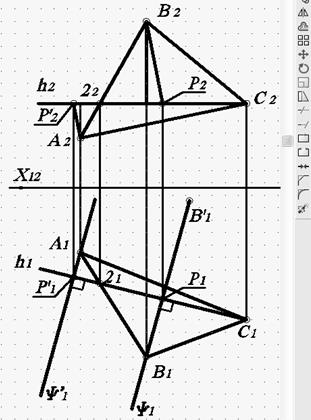
Рис. 79. Построение проекции плоскости ψ’₁

Решение задачи 1-м и 2-м способом продолжается построениями для вращения точки А вокруг линий уровня. Для 1-го способа вводится проекция плоскости, в которой вращается точка А (Δ’₂, рис. 78),
а для 2-го способа вводится проекция плоскости ψ’₁ (рис. 79). Последующие построения повторяются аналогично построениям для вращения точки В и заканчиваются построениями отрезков О’₂A’₂ для 1-го способа, Р’₁A’₁ для 2-го способа (рис. 80, 81).

 

 

Рис. 80. Построение отрезков О’₂A’₂

 

 

 

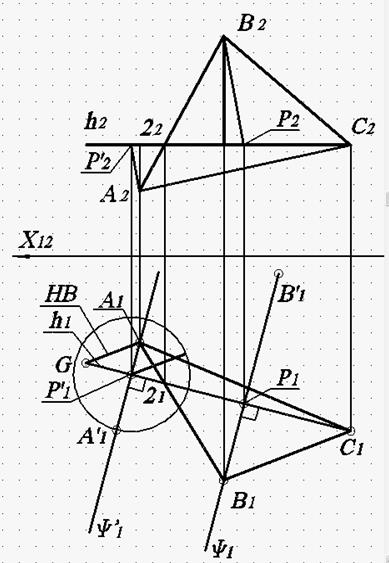
Рис. 81. Построение отрезков Р’₁A’₁

 

 

Наконец, для обоих способов выполняются построения конечных результатов (натуральных величин плоскостей) с использованием команды «Отрезок» путем соединения новых проекций точек A’₁, В’₁ и С₁ (рис. 82, 83).

Как предполагалось, новые проекции для построений 1-м и 2-м способом повернуты относительно друг друга. Измеряются площади обоих результатов поочередно.

Результаты измерения площадей треугольников, построенных
1-м и 2-м способом и форматы командной строки выполнения команды «Площадь» приведены на рис. 84 и 85.

Измерения площади совпадают с точностью до 4-го знака. Сравнение измерений площади натуральной величины плоскости, построенной обоими методами, показывает, что задача решена верно.

 

Рис. 82. Результат построения

натуральной величины плоскости первым методом

 

 

 

Рис. 83. Результат построения

натуральной величины плоскости вторым методом

 

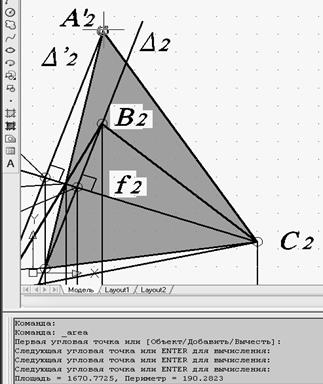
Рис. 84. Результат измерения площади

натуральной величины треугольника,

построенного первым способом

 

 

 

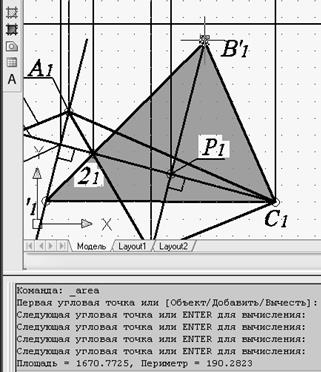
Рис. 85. Результат измерения площади

натуральной величины треугольника,

построенного вторым способом

Вариант 9

Дано: прямая AB (А₁ В₁; А₂ В₂). A₁(74;139); A₂(74;175); В₁(176;97); В₂(176;245); точка М₁(103;145); М₂(103;242).

Построить: натуральную величину расстояния от точки М до прямой АВ.

1. Решение выполнить:

– способом с использованием пересекающихся горизонтали и фронтали в Слое 1;

– способом перемены плоскостей проекций в Слое 2.

2. Проверить правильность решения задачи наиболее удобным способом.

3. Сравнить способы решения задачи и сделать вывод.

 

Вариант 10

Дано: плоскость АВС (А₁ В₁С₁; А₂ В₂С₂). А₁(67;112); А₂(67;188); В₁(92;152); В₂(92;217); С₁(125;125); С₂(125;168). Точка М (М₁; М₂). М₁(117;100); М₂(117;168).

Определить: расстояние от точки М до плоскости АВС.

1. Решение выполнить:

– способом с использованием пересекающихся горизонтали и фронтали;

– с использованием метода перемены плоскостей проекций.

2. Проверить правильность решения задачи путем сравнения результатов решения с применением команды «Расстояние».

3. Сравнить способы решения задачи и сделать вывод.