I.4. Состояния системы. Уравнения состояния системы

 

Каждому взаимодействию данного рода соответствует своя координата и свой потенциал, как было показано ранее. Так, для термодеформационной системы можно записать чет­вёрку параметров:

x	S	v
P	T	-p

 

Если система имеет n термодинамических степеней свободы, то есть допускает n взаимодействий различ­ного рода, то для такой системы можно записать n координат x₁, x₂,…,x_n и, соответственно, n потенциалов: P₁, P₂,…,P_n.

Совокупность координат и потенциалов общим числом 2n называется термодинамическими пара­метрами состояния системы.

Пример. Для термодеформационной системы n = 2, так как система допускает тепловое и дефор­мационное взаимодействии.

Как было установлено в ходе развития термодинамики, вся совокуп­ность координат состояния системы полностью характеризует состояние сис­темы. Так, внутренняя энергия системы

U = U(x₁, x₂,…,x_n)

Потенциалы также являются однознач­ными функциями всей совокупности координат системы, то есть

P_k = P_k(x₁, x₂,…,x_n) (13)

Уравнение (13) называется уравнением состояния системы в общем виде.

Рассмотрим термодеформационную систему, для которой (13) запишется как два уравнения:

T = T(S, v) и p = p(S, v).

Так как приборов для измерения эн­тропии нет, то желательно энтропию из этих уравнений исключить. Выразим S из первого уравнения, подставим во второе и окончательно получим

F(p, T, v) = 0 (14)

Уравнение (14) называется уравнением состояния термодеформационной системы в общем виде. Конкретный вид этого уравнения состояния системы классическая термодина­мика вследствие макроскопичности получить не может и вынуждена заимствовать у других наук.

Из физики известно уравнение состояния идеального газа (уравнение Менделеева-Клапейрона):

pv = RT (15)

Здесь, R, удельная газовая постоянная. R является индивидуальной характе­ристикой газа, содержится в справочной литературе или вычисляется через универсальную газовую постоянную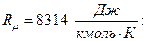

R = 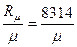, (16)

где μ – молярная масса.

Например, для воздуха μ = 28,96 и R= 8314/28,96= 287

 

Идеальный газ– это газ, молекулы которого не имеют объёма, отсутствуют силы межмолекулярного притяжения и ассоциации молекул. Таким образом, идеальный газ – это научная абстракция, в природе его нет.

При малых давлениях и высоких температурах любой газ можно услов­но считать идеальным и применять к нему уравнение состояния идеального газа. Чем выше давление и ниже температура, тем больше свойства газа откло­няются от свойств идеального газа. Уравнением (15) рекомендуется пользоваться, если давление газа не превышает 3 МПа. Чем выше давление, тем выше погрешность уравнения Менделеева-Клапейрона.

Уравнение состояния идеального газа записывется в различных формах.

pv_μ = R_μT (17)

Уравнение (17) было получено Д.И. Менделеевым;

Здесь, v_μ – молярный объём. Удельный объем и молярный объем связаны между собой соотношением

(18)

Если подставить в уравнение (17) соотношения (18) и (16), то получим pv = RT. В таком виде уравнение состояния идеального газа получил Клапейрон.

pW = MRT (19)

М – масса системы, кг; W – объем системы, м³.

 

(20)

где – число киломолей вещества системы.

Киломоль – это количество вещества в килограммах, численно равное его мо­лекулярной массе. Например, 1 кмоль воздуха (µ = 28,96) имеет массу 28,96 кг.

 

p = ρRT (21)

где ρ = 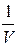, плотность, 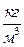(22)