II.4. Зависимость теплоёмкостей от давления, объёма и температуры

Ранее было получено,

dQ = T dS

dQ = c dT

Приравняем эти выражения и выразим массовую теплоемкость с:

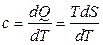откуда, как частные случаи, запишем массовые изохорные и изобарные теплоемкости

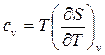(88)

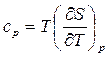(89)

Исследуем зависимость массовой изохорной теплоёмкости от величины объёма при Т=const. Из (88)

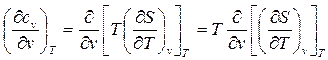(90)

Так как 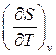не относится не к одному из типов дифференциальных соотношений термодинамики, то поменяем порядок дифференцирования:

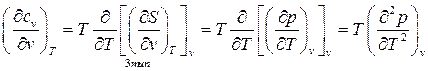(91)

Таким образом, изохорная теплоёмкость зависит от величины объёма системы (с_v=c_v(v)), если в уравнении состояния газа давление от температуры зависит нелинейно, т.е. 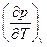¹ const. Если давление газа в уравнении состояния зависит от температуры линейно, то c_v ¹ c_v(v).

Исследуем зависимость изобарной теплоёмкости от величины давления при T=const. Из (89)

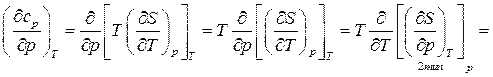
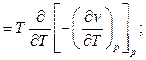
Окончательно

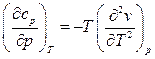(92)

Таким образом, изобарная теплоёмкость зависит от величины давления, если удельный объём в уравнении состояния зависит от температуры нелинейно, т.е.

при 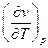¹const c_p=c_p(p)

И наоборот,

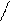при 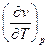=const, c_p=c_p(p)

В последнем случае не нужно опытным путем определять изобарную теплоемкость в лабораторных установках при различных значениях давления.

Все полученные в этом параграфе формулы относятся как к реальным, так и идеальным газам.

Исследуем идеальный газ, используя формулы (91), (92):

,

.

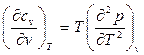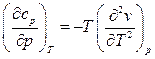Из (77) для идеального газа .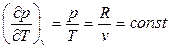

Тогда из (91) 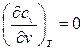, следовательно, изохорная теплоёмкость идеального газа от величины объёма не зависит (c_v ¹ c_v(v)).

Исследуем зависимость изобарной теплоёмкости от величины давления:

Из (78) 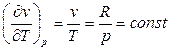. Тогда из (91) 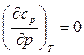, следовательно, изобарная теплоемкость идеального газа от величины давления не зависит (c_p ¹c_p(p)).

Исследуем зависимость изохорной теплоёмкости от величины давления, то есть найдем 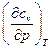, представив ее в виде произведения двух частных производных

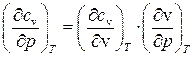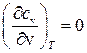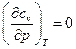. Так как , а сжимаемость , то или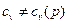

Исследуем зависимость изобарной теплоемкости от величины объема:

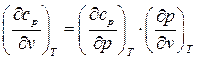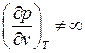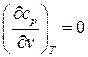, так как , а или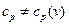

Исследуем зависимость изохорной и изобарной теплоёмкости от величины температуры:

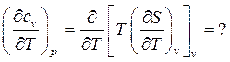
Поменять порядок дифференцирования и применить затем дифференциальные соотношения термодинамики в этом случае не удается, то есть термодинамика на этот вопрос не отвечает. Получить зависимость изохорной теплоёмкости от температуры можно либо опытным путём, либо с помощью какой-либо физической теории.

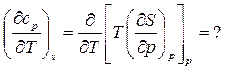
Как и в предыдущем случае термодинамика на этот вопрос не отвечает. Зависимость изобарной теплоемкости от температуры определяется либо опытным путём, либо с помощью какой-либо физической теории.