I.2. Теплота, работа, внутренняя энергия

 

Обозначим через Q_k количество взаимодействия - меру взаимодействия между системой и окру­жающей средой. Так, при тепловом взаимодействии, количеством взаимодействия является теплота. Размерность Q_k зависит от вида взаимодействия.

Обозначим через Q, 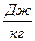удельную теплоту, которой обмениваются окружающая среда и система.

Обозначим через A, 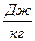удельную абсолютную работу. Работа А подразделяется на механическую и немеханическую.

Абсолютная деформационная работа в координатах рv изображается графически как площадь под кривой (прямой) процесса по отношению к оси v.

Р

 

Р_{1 1}

 

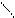
Р_{2 2}

 

V₁ V₂ V

рис.2

Примечание: кроме абсолютной работы А в термодинамике также используется понятие располагаемой (полезной) работы А_пол - работы, которая может быть «передана» другой системе. Графически работа А_пол также изображается как площадь под кривой, но по отношению к оси р

Примеры немеханической работы:

1) работа химических реакций;

2) работа электрических сил.

В ходе развития термодинамики было установлено, что единственными формами передачи энергии являются теплота и ра­бота. Строго говоря, работа и теплота это не виды энергии, так как проявляются только в процессе передачи энергии.

Обозначим через U, 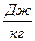удельную внутреннюю энергию системы.

Внутренняя энергия включает в себя кинетическую энергию по­ступательного и колебательного, вращательного движения молекул, потенциальную энергию межмолекуляр­ного взаимодействия, а также химическую и атомную энергию.

Обозначим через Е, E_кин, E_p соответственно полную, кинетическую и потенциальную энергию системы:

E = E_кин + E_p + U.

В термодинамике все результаты получены для случая, когда

E_кин = 0 и E_p = 0, таким образом полагается, что полная энергия системы равна внутренней, то есть:

E = U.

В ходе развития термодинамики были установлены соотношения:

dQ_k = (1)

dA_k = – dQ_k = – (2)

Например, при тепловом взаимодействии:

dQ = T dS (3)

При деформационном:

dA_деф = – dQ_k = = (4)

У системы с E = U все взаимодействия системы с окружающей средой со­провождаются изменением внутренней энергии системы, то есть математически это выражается следующей формулой:

dU = = (5)

Формула (5) - первое начало термодинамики в обобщённом виде.

Здесь n – число термодинамических степеней свободы системы, т.е. количество взаимодействий разного рода, которые допускает данная система.

Например, у деформационной системы есть только одна степень свободы, а именно дефор­мационная (механическая). Для такой системы первое начало термодинамики запи­шется в следующем виде:

dU = dQ_деф = - р^(l)dv (6)

Система, которая допускает ее деформирование и теплообмен с окружающей средой называется термодеформационной системой (тепломеханической). У такой системы две степени свободы (n=2):

dU = dQ_деф + dQ (7)

Так как dQ_деф = -dA_деф , а dQ = T^(l)dS уравнение (5) примет следующий вид:

dU = p^(l)dv+ T^(l)dS (8)

Уравнение (8) - это первое начало термодинамики для термодеформационной системы.