Решение
Составим ряд из абсолютных величин членов данного ряда: 
. Исследуем его на сходимость.
Сравним данный ряд с гармоническим рядом 
.
, 
.
Найдем 
.
Предел конечный и отличный от нуля.
Так как гармонический ряд расходится, то расходится и ряд согласно признака сравнения. Следовательно данный ряд не является абсолютно сходящимся.
Применим к данному знакочередующемуся ряду признак Лейбница.
Найдем разность 
;
,
так как 
при любом 
, 
при любом и 
при любом .
Первое условие Лейбница выполнено: 
. Проверим второе условие признака Лейбница: 
. Значит данный ряд сходится.
Причем он является условно сходящимся.
5. Найти область сходимости степенного ряда:
Решение
Найдем интервал сходимости ряда и исследуем поведение ряда на концах интервала сходимости. Применим к ряду из модулей признак Даламбера, при фиксированном x:
; 
Найдем предел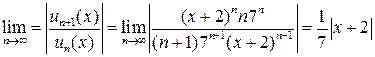 
Если 
, то 
, 
, 
.
Интервалом сходимости является интервал 
.
Исследуем поведение ряда на концах интервала .
При 
имеем ряд 
.
Этот ряд расходится.
При х=9 получаем ряд 
Применим к данному ряду признак Лейбница.
Очевидно выполнение обоих условий: 
, 
.
Ряд 
сходится условно, так как ряд из абсолютных величин 
расходится.
Следовательно, областью сходимости ряда является промежуток 
.
6. Найти разложение функции в степенной ряд по степеням x:
.
Решение
Используем разложение функции 
:
Заменяя в этой формуле 
на 
, получаем 
Полученный ряд сходится при всех , т.е. при 
Разложение имеет вид:
7. Используя разложение подынтегральной функции в степенной ряд, вычислить определенные интегралы с указанной погрешностью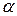 
:
, 
Решение
Применим ряд для 
:
Заменим на 
:
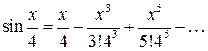
Разделив почленно ряд для 
на , получим
Интегрируя этот ряд почленно (это возможно, так как пределы интегрирования принадлежат интервалу сходимости данного ряда), получим
Поскольку этот ряд удовлетворяет признаку Лейбница:
1. 
, 2. , то погрешность при замене суммы такого ряда суммой его первых 
членов не превышает модуля первого отброшенного члена.
Ограничиваясь первыми двумя членами этого ряда, находим
8. найти разложение в степенной ряд по степеням решения дифференциального уравнения (записать три первых, отличных от нуля, члена этого разложения)
, 
.
Решение
Искомое решение запишем в виде ряда Моклорена
……………………… 
Подставляя найденные значения производных в ряд, получим искомое решение дифференциального уравнения.
- искомое решение.
Литература
1. Пискунов Н.С. «Дифференциальное и интегральное исчисления для втузов», М., 1960.
2. Шнейдер В.Е., Слуцкий А.И., Шумов А.С. «Краткий курс высшей математики 1, 2», М. 1978.
3. «Задачи и упражнения по математическому анализу для втузов». Под редакцией Б.П. Демидовича. М., 1960.
Содержание
Вопросы учебной программы третьего семестра ………………………………………….3
Основные формулы и теоремы………………………………………………………………..4
Типовые задания…………………………………………………………………………………7
Задания к аттестационной работе №3 по теме: «Кратные и криволинейные интегралы»…………………………………………………………………………………………8
Решение типового варианта……………………………………………………………………17
Задания к аттестационной работе №3 по теме: Ряды.……………………………………22
Решение типового варианта……………………………………………………………………33
Учебное издание
Составители: Пархимович Игорь Владимирович
Гоголинская Рената Альфонсовна
Остапчук Евгений Матвеевич
