Измените порядок интегрирования.

| |
 
| |
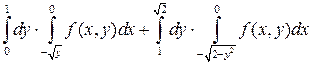
| |

| |

| |

| |

| |
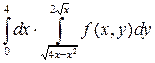
| |

| |
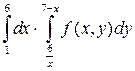
| |

| |

| |

| |

| |

| |

| |
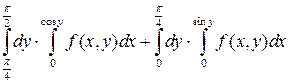
| |

| |

| |
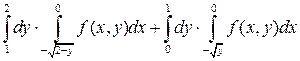
| |

| |
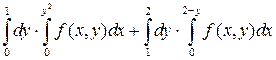
| |
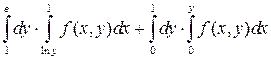
| |

| |
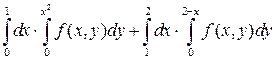
| |
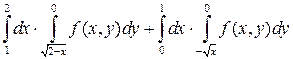
| |

| |

| |

| |

|
Найти площадь фигуры, ограниченной данными линиями
а). 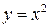 , , 
| б). 
| |
а).  , , 
| б). 
| |
а).  , , 
| б). 
| |
а). 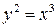 , ,  , , 
| б). 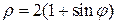
| |
а).  , , 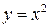
| б). 
| |
а).  , ,  , , 
| б). 
| |
а).  , , 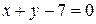
| б). 
| |
а).  , ,  , ,  , , 
| б). 
| |
а).  , , 
| б). 
| |
а).  , ,  , , 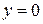
| б). 
| |
а).  , ,  , , 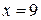
| б). 
| |
а)  , ,  , , 
| б) 
| |
а) 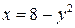 , , 
| б) 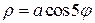
| |
а)  , ,  , ,  , , 
| б) 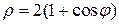
| |
а) 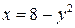 , , 
| б) 
| |
а)  , ,  , , 
| б) 
| |
а)  , , 
| б) 
| |
а)  , , 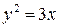
| б) 
| |
а)  , , 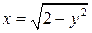
| б) 
| |
а)  , ,  , , 
| б) 
| |
а) 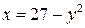 , , 
| б) 
| |
а)  , ,  , , 
| б) 
| |
а)  , ,  , , 
| б) 
| |
а)  , ,  , , 
| б) 
| |
а)  , ,  , ,  , , 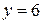
| б) 
| |
а)  , ,  , , 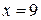
| б) 
| |
а)  , , 
| б) 
| |
а)  , , 
| б) 
| |
а) 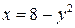 , , 
| б) 
| |
а)  , ,  , ,  , , 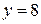
| б) 
|
Вычислить двойной интеграл
Вариант
 ; ;  , , 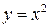 , ,  
| |
 ; ;  , ,  , , 
| |
 ; ;  , , 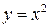 , , 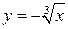
| |
 ; ;  , , 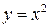 , , 
| |
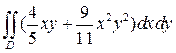 ; ;  , ,  , , 
| |
 ; ;  , ,  , ,  , , 
| |
 ; ;  , ,  , , 
| |
 ; ;  , ,  , , 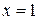 , , 
| |
 ; ;  -треугольник с вершинами -треугольник с вершинами  , , 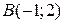 , , 
| |
 ; ;  -треугольник с вершинами -треугольник с вершинами  , ,  , , 
| |
 ; ;  -определена неравенствами -определена неравенствами  , , 
| |
 ; ;  , ,  , ,  , ,  , ,  , , 
| |
 ; ; 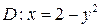 , , 
| |
 ; ;  , , 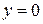 , , 
| |
 ; ;  , , 
| |
 ; ;  -определена неравенствами -определена неравенствами  , , 
| |
 ; ;  , ,  , , 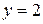
| |
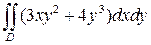 ; ;  - прямоугольник - прямоугольник 
| |
 ; ;  - прямоугольник - прямоугольник 
| |
 ; ;  , ,  , ,  , , 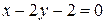
| |
 ; ;  , ,  , ,  , , 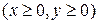
| |
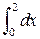 
| |
 
| |
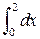 
| |
 ; ;  - определена неравенствами - определена неравенствами  , , 
| |
 ; D – круговой сектор, ограниченный линиями: ; D – круговой сектор, ограниченный линиями:  , ,  , , 
| |
 ; D: ; D: 
| |
 ; D: ; D:  , ,  , ,  , , 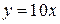
| |
 ; D: ; D:  , ,  , ,  , , 
| |
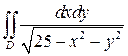 ; D – круг ; D – круг 
|
Вычислить криволинейный интеграл второго рода по данной линии в указанном направлении.
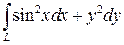 ; L – дуга линии ; L – дуга линии  , , 
| |
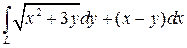 ; L – дуга линии ; L – дуга линии 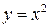 от A(0;0) до B(1;1) от A(0;0) до B(1;1)
| |
 ; L – отрезок прямой от A(1;1) до B(2;2) ; L – отрезок прямой от A(1;1) до B(2;2)
| |
 ; L – дуга линии ; L – дуга линии  , , 
| |
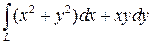 ; L – дуга кривой ; L – дуга кривой  от A(0;1) до B(1;е) от A(0;1) до B(1;е)
| |
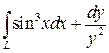 ; L – дуга кривой ; L – дуга кривой  от от  до до 
| |
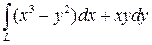 ; L – дуга кривой ; L – дуга кривой  от A(0;1) до B(1;а) от A(0;1) до B(1;а)
| |
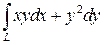 ; L – дуга кривой ; L – дуга кривой  , ,  , , 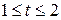
| |
 ; L – дуга кривой ; L – дуга кривой 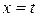 , ,  , , 
| |
 ; L – дуга окружности ; L – дуга окружности  , ,  , , 
| |
 ; L – дуга эллипса ; L – дуга эллипса  , ,  , , 
| |
 ; L – дуга кривой ; L – дуга кривой 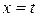 , ,  , ,  , , 
| |
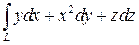 ; L – дуга кривой ; L – дуга кривой 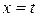 , ,  , ,  , , 
| |
 ; L – отрезок прямой от A(0;0;0) до B(1;1;1) ; L – отрезок прямой от A(0;0;0) до B(1;1;1)
| |
 ; L – дуга кривой ; L – дуга кривой 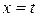 , ,  , ,  , , 
| |
 ; L – дуга кривой ; L – дуга кривой 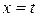 , ,  , ,  , , 
| |
 ; L – отрезок прямой от A(0;0;0) до B(1;1;1) ; L – отрезок прямой от A(0;0;0) до B(1;1;1)
| |
 ; L – дуга линии ; L – дуга линии 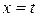 , ,  , ,  , , 
| |
 ; L – окружность ; L – окружность 
| |
 ; L – эллипс ; L – эллипс 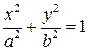
| |
 ; L – дуга параболы ; L – дуга параболы  от A(0;0) до B(1;2) от A(0;0) до B(1;2)
| |
 ; L – дуга эллипса ; L – дуга эллипса  , ,  против хода часовой стрелки. против хода часовой стрелки.
| |
 ; LABO – ломанная ABO, О(0;0), A(1;2), B( ; LABO – ломанная ABO, О(0;0), A(1;2), B(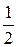 ;3) при положительном обходе ;3) при положительном обходе
| |
 ; L – отрезок прямой от О(0;0) до A(1;2) ; L – отрезок прямой от О(0;0) до A(1;2)
| |
 ; L – дуга параболы ; L – дуга параболы  , расположенная под осью ОХ и пробегающая по ходу часовой стрелки , расположенная под осью ОХ и пробегающая по ходу часовой стрелки
| |
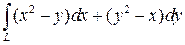 ; L – отрезок прямой от A(1;2) до B(3;6) ; L – отрезок прямой от A(1;2) до B(3;6)
| |
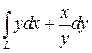 ; L – кривая ; L – кривая  от A(0;1) до B(-1;е) от A(0;1) до B(-1;е)
| |
 ; L – дуга верхней половины эллипса ; L – дуга верхней половины эллипса  , , 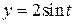 , по ходу часовой стрелки , по ходу часовой стрелки
| |
 ; L – дуга параболы ; L – дуга параболы 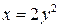 от А(0;0) до В(2;1) от А(0;0) до В(2;1)
| |
 ; L – окружность ; L – окружность 
|
С помощью тройного интеграла найти объем тела, ограниченного заданными поверхностями. Сделайте чертеж.
Вариант
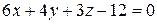 , ,  , , 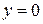 , , 
| |
 , ,  , ,  , , 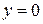 , , 
| |
 , ,  , ,  , , 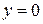 , , 
| |
 , ,  , ,  , , 
| |
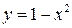 , ,  , ,  , , 
| |
 , ,  , ,  , , 
| |
 , , 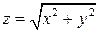 , ,
| |
 , , 
| |
 , , 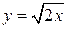 , ,  , , 
| |
 , ,  , , 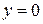 , ,  , , 
| |
 , ,  , ,  , , 
| |
 , ,  , ,  , , 
| |
 , , 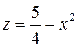 , , 
| |
 , , 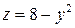 , , 
| |
 , ,  , , 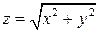 , , 
| |
 , ,  , , 
| |
 , ,  , ,  , , 
| |
 , ,  , ,  , , 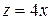 , , 
| |
 , , 
| |
 , ,  , , 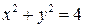
| |
 , ,  , , 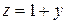
| |
 ; ;  , , 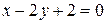 , , 
| |
 ; ; 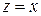 , , 
| |
 ; ;  ; ;  , , 
| |
 ; ;  , , 
| |
 , ,  , , 
| |
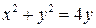 , ,  , , 
| |
 , ,  , ,  , , 
| |
 , ,  , , 
| |
 , , 
|
Решение типового варианта
1. Изменить порядок интегрирования:

Решение.

Для первого интеграла область интегрирования ограничена линиями  ,
, 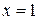 ,
, 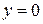 ,
,  и представляем криволинейную фигуру ОАВ.
и представляем криволинейную фигуру ОАВ.
Для второго интеграла область интегрирования ограничена линиями 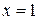 ,
,  ,
, 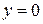 ,
, 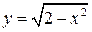 . Уравнение
. Уравнение 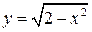 можно преобразовать к виду
можно преобразовать к виду  (верхняя дуга окружности т.к.
(верхняя дуга окружности т.к.  ).
).
Окружность  и прямая
и прямая  , при условии
, при условии  , пересекаются в точке А(1;1).
, пересекаются в точке А(1;1).
Данную сумму интегралов можно записать в виде одного повторного интеграла с областью интегрирования ОАС.

2. Найти площадь фигуры, ограниченной данными линиями.
а).  ,
, 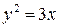
Решение

Площадь 
Данная область ограничена снизу параболой  , сверху – параболой
, сверху – параболой 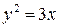 . Параболы пересекаются в точках О(0;0) и А(3;3).
. Параболы пересекаются в точках О(0;0) и А(3;3).
 (кв.ед.)
(кв.ед.)
б). 
Решение
Так как  , то
, то  . То есть
. То есть  . Изобразим фигуру, ограниченную данной линией:
. Изобразим фигуру, ограниченную данной линией:

Полюс О лежит на границе области D, поэтому площадь фигуры равна:
 =
=
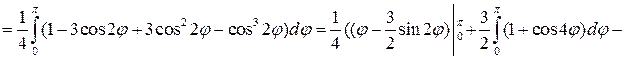
 (кв.ед.)
(кв.ед.)
3. Вычислить двойной интеграл.
 ;
;  ,
, 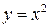
Решение Изобразим область D в прямоугольной системе координат:

Область D ограничена снизу параболой 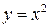 , а сверху – прямой
, а сверху – прямой  . Тогда:
. Тогда:




4.Вычислить криволинейный интеграл второго рода
 ;
;  ,
,  ,
,  .
.
Решение.
Равенства  ,
,  ,
,  задают астроиду. Изобразим астроиду в прямоугольной системе координат:
задают астроиду. Изобразим астроиду в прямоугольной системе координат:

Поскольку  ,
,  , то
, то




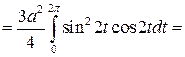


5. С помощью тройного интеграла найти объем тела, ограниченного заданными поверхностями.
 ,
, 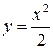 ,
,  .
.
Решение.

Равенства  ,
, 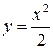 задают цилиндрические поверхности, а
задают цилиндрические поверхности, а  - плоскость. Область интегрирования V получается в результате пересечения параболы
- плоскость. Область интегрирования V получается в результате пересечения параболы 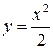 с линией пересечения цилиндра
с линией пересечения цилиндра  и плоскости
и плоскости  , т.е. с прямой
, т.е. с прямой 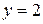 . Сверху тело ограничено цилиндрической поверхностью
. Сверху тело ограничено цилиндрической поверхностью  .
.
Ввиду симметрии тела относительно плоскости  вычисляем половину искомого объема:
вычисляем половину искомого объема:


Следовательно, 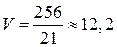 (куб.ед.)
(куб.ед.)
Задания к аттестационной работе №3 по теме: «Ряды»
№1 Найти сумму ряда:

| 
| 
|

| 
| 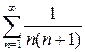
|
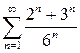
| 
| 
|
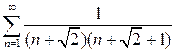
| 
| 
|

| 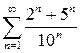
| 
|

| 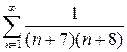
| 
|
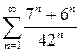
| 
| 
|
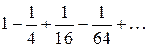
| 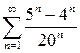
| 
|

| 
| 
|

| 
| 
|
№2 Исследовать на сходимость ряды с положительными членами:
а)  б) б)  в)
в)  г) г) 
| а)  б) б)  в)
в)  г) г) 
| |
а)  б) б)  в)
в)  г) г) 
| а)  б) б) 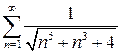 в)
в) 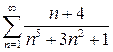 г) г) 
| |
а)  б) б)  в)
в)  г) г) 
| а)  б) б)  в)
в) 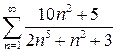 г) г) 
| |
а)  б) б)  в)
в)  г) г) 
| а) 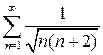 б) б)  в)
в) 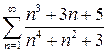 г) г) 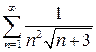
| |
а) 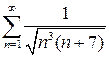 б) б)  в)
в)  г) г) | ||
|
|
|
|
|
|
Дата добавления: 2016-07-29; Мы поможем в написании ваших работ!; просмотров: 802 | Нарушение авторских прав
Лучшие изречения:






