МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ
«БРЕСТСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
Кафедра высшей математики
Кратные и криволинейные интегралы.
Ряды.
Методические указания и задания аттестационных работ
по курсу «Высшая математика»
для студентов строительного факультета.
Брест 2008
УДК 517.9
Кратные и криволинейные интегралы. Ряды.
Методические указания аттестационных работ по курсу "Высшая математика" для студентов строительного факультета, Брест, УО "БГТУ", 2008.
В соответствии с действующей программой для студентов строительного факультета составлены две аттестационные работы с индивидуальными заданиями и даны образцы их решения.
Составители: Пархимович И.В.,к.ф-м.н., доцент
Гоголинская Р.А. ассистент
Остапчук Е.М. ассистент
Рецензент: Доцент кафедры математического анализа и дифференциальных уравнений Учреждения образования "Брестский государственный университет
им. А.С. Пушкина", к.ф.—м.н. Дежурко Ю.И.
Учреждение образования
© «Брестский государственный технический университет 2008
Вопросы учебной программы (III семестр)
1. Задачи, приводящие к понятию двойного интеграла.
2. Определение, теоремы существования двойного интеграла. Свойства двойного интеграла.
3. Вычисление двойного интеграла в декартовой системе координат.
4. Замена переменных в двойном интеграле. Переход в двойном интеграле от декартовых к полярным координатам.
5. Приложения двойного интеграла - площадь плоской фигуры, объемы тел, статические моменты и центр тяжести. Момент инерции плоской фигуры.
6. Тройной интеграл: определение, свойства, вычисление в декартовых координатах.
7. Цилиндрические и сферические координаты. Переход в тройном интеграле от декартовых к цилиндрическим и сферическим координатам.
8. Приложения тройного интеграла — объемы тел, масса тел, центр тяжести.
9. Криволинейный интеграл 1-го рода (КрИ-I): определение, свойства, вычисление, приложения.
10. Криволинейный интеграл 2-го рода (КрИ-II): определение, свойства, вычисление, приложения.
11. КрИ-II по замкнутому контуру. Формула Грина. Независимость КрИ-II от формы пути интегрирования.
12. Общие понятия числового ряда. Геометрическая прогрессия и гармонический ряд.
13. Основные свойства сходящихся рядов. Необходимый признак сходимости рядов.
14. Признаки сравнения.
15. Признаки Даламбера и Коши.
16. Интегральный признак Коши. Ряд Дирихле.
17. Знакопеременные ряды. Признак Лейбница.
18. Абсолютно и условно сходящиеся ряды.
19. Равномерная сходимость функционального ряда. Признак Вейерштрасса. Свойства равномерно сходящихся рядов.
20. Степенные ряды. Теорема Абеля.
21. Свойства степенных рядов
22. Разложение функций и степенный ряд. Ряд Тейлора.
23. Разложение и ряд Тейлора-Маклорена элементарных функций ех, cosx, sinx,
 ,
, 
24. Приложение степенных рядов: приближенное вычисление значений функции, приближенное вычисление определенных интегралов, решение дифференциальных уравнений с помощью степенных рядов.
25. Тригонометрический ряд Фурье. Коэффициенты Фурье.
26. Сходимость ряда Фурье. Теорема Дирихле.
27. Ряды Фурье для четных и нечетных функций.
28. Разложение в ряд Фурье периодических функций с общим периодом. Разложение в ряд Фурье непериодических функций.
29.Виды уравнений математической физики. Метод Фурье. Метод сеток.
Основные формулы и теоремы
1.  , где обл. D – правильная и [a,b] - проекция обл. D на ОХ, и у = φ1(х) и у = φ2 (х)- графики функций, ограничивающих обл. D на OY,
, где обл. D – правильная и [a,b] - проекция обл. D на ОХ, и у = φ1(х) и у = φ2 (х)- графики функций, ограничивающих обл. D на OY,
x = ψ1(y) и х = ψ2 (y) – графики функций, ограничивающие обл. D слева и справа.
2. Двойной интеграл в полярных координатах:
 , где
, где  - раствор угла, содержащий обл. D, а r = r1(φ) r = r2(φ) – линии, ограничивающие область D.
- раствор угла, содержащий обл. D, а r = r1(φ) r = r2(φ) – линии, ограничивающие область D.
3. Площадь плоской фигуры D:


4. Объем цилиндрического тела

5. 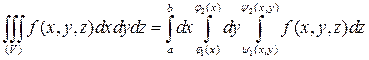 , где
, где

 - поверхности, ограничивающие обл. V снизу и сверху;
- поверхности, ограничивающие обл. V снизу и сверху;
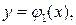
 - линии, ограничивающие снизу и сверху проекцию обл. V на
- линии, ограничивающие снизу и сверху проекцию обл. V на
пл. XOY, [a,b], - проекция на ось ОХ проекции обл. V на плоскости XOY.
6. 
7.  где
где

 – параметрические уравнения кривой АВ.
– параметрические уравнения кривой АВ.
8.  где x=x(t), y=y(t), z=z(t)
где x=x(t), y=y(t), z=z(t)
 – параметрические уравнения кривой АВ.
– параметрические уравнения кривой АВ.
9. 
 .
.
где x=x(t), y=y(t), z=z(t),  – параметрические уравнения кривой АВ.
– параметрические уравнения кривой АВ.
10. 
где 
 – уравнение кривой АВ.
– уравнение кривой АВ.
11. 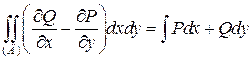 – формула Грина
– формула Грина
12. u1 + u2 + … + un + … = 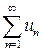 – ряд
– ряд
Sn = u1 + u2 + … + un – частичная сумма ряда
S =  Sn – сумма ряда.
Sn – сумма ряда.
13. a + aq + aq2 + … + aqn-1 + … – геометрическая прогрессия, при │q│< 1 – г.п. сходится
14.  – гармонический ряд расходится
– гармонический ряд расходится
15. Если ряд 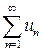 сходится, то
сходится, то 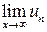 = 0 – необходимый признак сходимости ряда.
= 0 – необходимый признак сходимости ряда.
16. Пусть 
а) если ряд  сходится, то сходится ряд
сходится, то сходится ряд 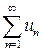
б). если ряд 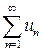 расходится, то расходится ряд
расходится, то расходится ряд 
17. Пусть 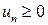 и
и 
Если 
 , то оба ряда
, то оба ряда 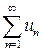 и
и  сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
18. Пусть 

а) если 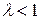 , то ряд
, то ряд 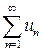 сходится
сходится
б). если  , то ряд
, то ряд 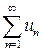 расходится - признак Даламбера
расходится - признак Даламбера
19. Пусть 

а) если 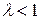 , то ряд
, то ряд 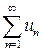 сходится
сходится
б). если  , то ряд
, то ряд 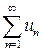 расходится - признак Коши
расходится - признак Коши
20. Если интеграл  сходится, то сходится и ряд
сходится, то сходится и ряд 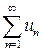 , а если интеграл
, а если интеграл
 расходится, то расходится и ряд
расходится, то расходится и ряд 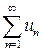 , где f(x) – непрерывная, положительная, монотонно убывающая функция, и un = f(n) – интегральный признак Коши.
, где f(x) – непрерывная, положительная, монотонно убывающая функция, и un = f(n) – интегральный признак Коши.
21. Если члены знакочередующегося ряда 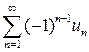 монотонно убывают по абсолютной величине и
монотонно убывают по абсолютной величине и 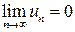 , то данный ряд сходится, его сумма положительная и не превосходит первого члена – признак Лейбница.
, то данный ряд сходится, его сумма положительная и не превосходит первого члена – признак Лейбница.
22.  область сходимости
область сходимости 
 область сходимости
область сходимости 


 (-1; 1]
(-1; 1]
 (-1;1)
(-1;1)
23.  - тригонометрический ряд
- тригонометрический ряд


 - коэффициент Фурье.
- коэффициент Фурье.
Типовые задания
1. Изменить порядок интегрирования 
2. Вычислить  где D – область, ограниченная линиями y=x, y=2x, x=2, x=3.
где D – область, ограниченная линиями y=x, y=2x, x=2, x=3.
3. Вычислить  где D – область, ограниченная линией
где D – область, ограниченная линией 
4. Вычислить площадь фигуры, ограниченной линиями 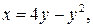

5. Найти объем тела, ограниченного поверхностями 

6. Вычислить  где V – область, ограниченная плоскостями x=0, y=0, z=0, x+y+z-2=0
где V – область, ограниченная плоскостями x=0, y=0, z=0, x+y+z-2=0
7. Вычислить  где L – отрезок прямой от А(0;0) до В(4;3)
где L – отрезок прямой от А(0;0) до В(4;3)
8. Вычислить 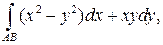 где АВ – отрезок прямой от А(1;1) до В(3;4)
где АВ – отрезок прямой от А(1;1) до В(3;4)
9. Найти сумму ряда 
10. Исследовать на сходимость ряды:
а)  б)
б) 
в)  г)
г) 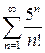
д)  е)
е) 
11. Найти область сходимости ряда: 
12. Разложить в ряды по степеням х:
а)  б)
б) 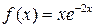
13. Разложить в ряд Фурье периодическую функцию  с периодом
с периодом  , заданную в интервале
, заданную в интервале  уравнением
уравнением 
Задания к аттестационной работе №3 по теме:






