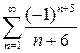
| 
| 
| 
|
| 
| 
| 
|
| 
| 
| 
|
| 
| 
| 
|
| 
| 
| 
|
| 
| 
| 
|
| 
| 
| 
|
| 
|
Найти область сходимости степенного ряда.
| 
| 
| 
|
| 
| 
| 
|
| 
| 
| 
|
| 
| 
| 
|
| 
| 
| 
|
| 
| 
| 
|
| 
| 
| 
|
| 
|
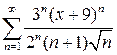
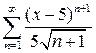
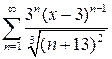
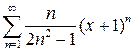
Найти разложение функции в степенной ряд по степеням x
| 
| 
| 
|
| 
| 
| 
|
| 
| 
| 
|
| 
| 
| 
|
| 
|
| 
|
|
| 
| 
|
| 
| 
| 
|
|
|
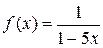
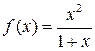
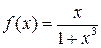
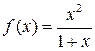
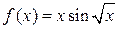
№7 Используя разложение подынтегральной функции в степенной ряд, вычислить определенные интегралы с указанной погрешностью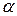 
:
 
|  
| 
| 
|
| 
| 
| 
|
| 
| 
| 
|
| 
| 
| 
|
| 
| 
| 
|
| 
|
| 
|
| 
| 
|
|
| 
|
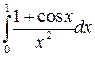
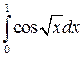
№8 Найти разложение в степенной ряд по степеням x решения дифференциального уравнения(записать три первых, отличных от нуля, члены этого разложения):
| 
| 
| 
|
| 
| 
| 
|
| 
| 
| 
|
| 
| 
| 
|
| 
| 
| 
|
| 
| 
| 
|
| 
| 
| 
|
| 
|
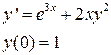
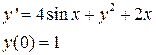
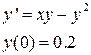
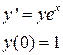
Решение типового варианта
1. Найти сумму ряда:
Решение
Составим n-ую частичную сумму данного ряда:
Чтобы упростить выражение для 
, преобразуем формулу для общего члена ряда, разлагая 
на элементарные дроби. Положим
отсюда
Сравнивая коэффициенты при одинаковых степенях n в числителях обеих частей равенства, получаем:
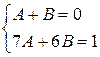откуда 
, 
, поэтому
Выражение для принимает вид
Приводя подобные члены, получаем
Переходя к пределу, находим 
Следовательно
Исследовать на сходимость ряды с положительными членами
а) 
Решение
Сравним данный ряд с гармоническим рядом 
. Выпишем общие члены рядов: 
, 
. Найдем 
Предел конечный и отличный от нуля.
Так как гармонический ряд расходится, то на основании признака сравнения заключаем, что данный ряд также расходится.
б) 
Решение
Сравним данный ряд с рядом Дирихле 
. Так как 
, то ряд сходится.
Согласно признака сравнения данный ряд сходится.
в) 
Решение
, 
, 
, 
Поскольку 
, сравним данный ряд с рядом 
, который является рядом Дирихле и сходится, т.к. 
, 
.
Предел конечный и отличный от нуля.
Согласно признака cравнения данный ряд сходится.
г) 
Решение
Сравним данный ряд с рядом Дирихле 
, который сходится, т.к. 
, .
Согласно признака сравнения данный ряд сходится.
3. Исследовать на сходимость ряды с положительными членами:
а) 
Решение.
Применим интегральный признак Коши.
Функция 
удовлетворяет условиям интегрального признака Коши.
Поскольку 
, т.е. интеграл 
расходится, то расходится и данный ряд.
б)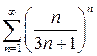 
Решение
Применим признак Коши. Поскольку 
, 
.
. Так как 
, ряд сходится.
в) 
Решение
Применим признак Даламбера. Поскольку 
; 
.
, то данный ряд сходится.
г) 
Решение
Применим признак Даламбера.
Так как 
, 
,
, то данный ряд сходится.
