—краткосрочный -0,67, долгосрочный 9,5, средний лаг 0,79
rss1=22,25
не подтверждаем
На основе квартальных данных получено уравнение множественной регрессии
y = - 0,55 + 0,088 x t1 – 4,77 x t2 + 5,4 x t3
и ESS = 110,32, RSS = 21,43. (ESS – объясненная сумма квадратов, RSS – остаточная сумма квадратов). Для этой же модели были раздельно проведены регрессии на основе данных:
1-й квартал 1991 г. - 1-й квартал 1995 г. и
2-й квартал 1995 г. – 4 квартал 1996 г., соответственно получены следующие значения сумм квадратов остатков RSS1 = 12,25, RSS2=2,32. Гипотеза о том, что произошли структурные изменения на уровне α =0,05:
—подтвердилась, т.к. F = 1,883, что больше F кр
+не подтвердилась, т.к. F = 1,883, что меньше F кр
—подтвердилась, F = 3,54, что больше F кр
На основе квартальных данных получено уравнение множественной регрессии
y = 1,55 + 1,4 x t1 – 0,77 x t2 + 2,4 x t3
и ESS = 92,32, RSS = 22,3. (ESS – объясненная сумма квадратов, RSS – остаточная сумма квадратов). Для этой же модели были раздельно проведены регрессии на основе данных:
1-й квартал 1991 г. - 1-й квартал 1995 г. и
2-й квартал 1995 г. – 4 квартал 1996 г., соответственно получены следующие значения сумм квадратов остатков RSS1 = 6,78, RSS2=2,2. Гипотеза о том, что произошли структурные изменения на уровне α =0,05:
+подтвердилась, т.к. F = 5,93, что больше F кр
—не подтвердилась, т.к. F = 1,883, что меньше F кр
—подтвердилась, т.к F = 3,54, что больше F кр
На основе квартальных данных с 1991 года по 1996 год с помощью МНК получено следующее уравнение:
Y t = 1,12 – 0, 0098 x t1 – 5, 62 x t2 + 0, 044 x t3
(2,14) (0,0034) (3,42) (0,009)
В скобках указаны стандартные ошибки, ESS (объясненная сумма квадратов) = 115, 32; RSS (остаточная сумма квадратов) = 25, 43
Когда в уравнение были добавлены три фиктивные переменные, соответствующие первым трем кварталам года, величина ESS выросла до 128, 20. Проверьте гипотезу о наличии сезонности при уровне значимости α = 0,05:
—гипотеза о наличии сезонности отвергается
Гипотеза о наличии сезонности принимается
—на основе имеющихся данных такую гипотезу проверить невозможно
На основе квартальных данных с 1991 года по 1996 год с помощью МНК получено следующее уравнение:
Y t = 1,12 – 0, 0098 x t1 – 5, 62 x t2 + 0, 044 x t3
(2,14) (0,0034) (3,42) (0,009)
В скобках указаны стандартные ошибки, ESS (объясненная сумма квадратов) = 116, 32; RSS (остаточная сумма квадратов) = 31, 43
Проверьте значимости коэффициентов и модели в целом при уровне значимости α = 0,05:
—все коэффициенты модели значимы и модель в целом также значима
Модель в целом значима, но часть коэффициентов незначима
—все коэффициенты незначимы и модель также статистически незначима
—на основе имеющихся данных проверить такие гипотезы невозможно
Система одновременных уравнений. Косвенный МНК (Задачи)
Дана следующая модель спроса и предложения:
Спрос:  ,
,  и
и  ,
,
Предложение:  ,
,  ,
,
где Q - количество продаваемых и покупаемых товаров, P - цена, Y - доход потребителей.
В этой модели экзогенной переменной является:
—Q
Y
—P и Y
—P
Имеется следующая структурная модель:
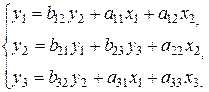
Соответствующая ей приведенная форма модели имеет вид:

Первое уравнение структурной формы имеет вид:
+ 
—уравнение неидентифицируемо, поэтому невозможно однозначно определить его коэффициенты
— 
— 
Имеется следующая структурная модель:

Соответствующая ей приведенная форма модели имеет вид:

Первое уравнение структурной формы имеет вид:
+ 
—уравнение неидентифицируемо, поэтому невозможно однозначно определить его коэффициенты
— 
— 
Имеется следующая структурная модель:

Ей соответствует приведенная форма:

В этом случае относительно 3 – го уравнения структурной формы можно записать следующее:
+ 
—уравнение сверхидентифицируемо, и для получения его параметров нет достаточной информации
— 
— 
Имеется следующая структурная модель:

Ей соответствует приведенная форма:

В этом случае относительно 3 – го уравнения структурной формы можно записать следующее:
+ 
—уравнение сверхидентифицируемо, и для получения его параметров нет достаточной информации
— 
— 
Имеется следующая структурная модель:

Ей соответствует приведенная форма:

В этом случае относительно 3 – го уравнения структурной формы можно записать следующее:
+ 
—уравнение сверхидентифицируемо, и для получения его параметров нет достаточной информации
— 
— 
Имеется следующая модель:

Она является:
Неиндетифицируемой
—Идентифицируемой
—сверхидентифицируемой, поскольку 1-е и 2-е уравнения идентифицируемы, а 3-е уравнение сверхидентифицируемо
—сверхидентифицируемой, поскольку 1-е и 2-е уравнения сверхидентифицируемы
Имеется следующая модель:

Она является:






