Средняя зарплата сотрудников меньше рекламируемой, а разброс в зарплатах больше на всех уровнях значимости

Эконометрика ЗАДАЧИ

Основные понятия теории вероятностей и статистики Задачи к экзамену.

Пусть X,Y – годовые дивиденды от вложений денежных средств в акции компаний А и В соответственно. Риск от вложений характеризуется дисперсиями: D(X)=25, D(Y)=16. Коэффициент корреляции σ = +0,8. Менее рискованно вкладывать денежные средства:

+ в отрасль В

—в отрасль А

—в обе отрасли в соотношении 30% на 70%

 

Пусть X,Y – годовые дивиденды от вложений денежных средств в акции компаний А и В соответственно. Риск от вложений характеризуется дисперсиями: D(X)=4, D(Y)=9. Коэффициент корреляции σ=0,7. Менее рискованно вкладывать денежные средства:

+ в отрасль А

—в отрасль В

—в обе отрасли в соотношении 40% на 60%

 

Пусть X,Y – годовые дивиденды от вложений денежных средств в акции компаний А и В соответственно. Риск от вложений характеризуется дисперсиями: D(X)=4, D(Y)=9. Коэффициент корреляции σ= -0,65. Менее рискованно вкладывать денежные средства:

+ в обе отрасли в соотношении 40% на 60%

—только в отрасль А

—только в отрасль В

 

Доход Х населения имеет нормальный закон распределения со средним значением 5000 руб. и средним квадратическим отклонением 1000 руб. Обследуется 1000 человек. Наиболее вероятное количество человек, имеющих доход более 6000 руб., будет составлять:

+ 158

—159

—341

—342

 

Доход Х населения имеет нормальный закон распределения со средним значением 4500 руб. и средним квадратическим отклонением 700 руб. Обследуется 500 человек. Наиболее вероятное количество человек, имеющих доход более 5500 руб., будет составлять:

+ 38

—39

—212

—213

 

Доход Х населения имеет нормальный закон распределения со средним значением 9000 руб. и средним квадратическим отклонением 800 руб. Обследуется 2000 человек. Наиболее вероятное количество человек, имеющих доход более 10400 руб., будет составлять:

+ 80

—81

—920

—921

 

Статистика по годовым темпам инфляции в стране за последние 10 лет составила (%): 2,6; 3,0; 5,2; 1,7; -0,5; 0,6; 2,2; 2,9; 4,2; 3,8. Несмещенные оценки среднего темпа инфляции, дисперсии и среднего квадратического отклонения составляют:

+ 2,57; 2,84; 1,69

—2,57; 2,56; 1,60

—2,57; 25,58; 5,06

 

Статистика по годовым темпам инфляции в стране за последние 10 лет составила (%): 2,3; 3,5; -0,8; 4,0; 2,4; 3,2; 4,1; 3,6; 2,5; 4,2. Несмещенные оценки среднего темпа инфляции, дисперсии и среднего квадратического отклонения составляют:

+ 2,9; 2,19; 1,48

—2,9; 2,06; 1,44

—2,9; 20,55; 4,53

 

Статистика по годовым темпам инфляции в стране за последние 10 лет составила (%): 3,8; 2,2; -0,7; -1,0; 4,2; 5,1; 2,6; 0,8; 2,9; 1,1. Несмещенные оценки среднего темпа инфляции, дисперсии и среднего квадратического отклонения составляют:

+ 2,1; 4,15; 2,04

—2,1; 3,73; 1,93

—2,1; 37,34; 6,11

 

Предполагается, что месячный доход граждан страны имеет нормальное распределение с математическим ожиданием m=500 $ и дисперсией σ²=22500. По выборке из 500 человек определен выборочный средний доход 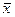=450 $. Доверительный интервал для среднедушевого дохода в стране составляют при уровне значимости 0,05:

+ 436,85; 463,15

—449,87; 450,13

—438,94; 461,06

 

При анализе зависимости между двумя показателями Х и Y по 30 наблюдениям получены следующие данные: 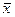= 105; 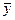=80; =900; 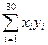=252600; =635. Оцените наличие линейной зависимости между Х и Y и статистическую значимость коэффициента корреляции ρ_хy:

+ r_xy=0,8; коэффициент значим на всех уровнях значимости

— r_xy= -0,8; коэффициент значим на всех уровнях значимости

— r_xy= 0,8; коэффициент не значим на всех уровнях значимости

— r_xy= 0,8; коэффициент значим только на уровне значимости 0,05

 

Предполагается, что месячная зарплата сотрудников фирмы составляет 500 $ при стандартном отклонении σ = 50 $. Выборка из 49 человек дала следующие результаты: 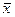=450$ и S = 60$. На основании результатов проведенных наблюдений можно утверждать, что:

+ средняя зарплата сотрудников меньше рекламируемой на всех уровнях значимости, а разброс в зарплатах больше на уровне значимости α=0,05 и α=0,1

—средняя зарплата сотрудников меньше рекламируемой на всех уровнях значимости, а разброс в зарплатах больше только на уровне значимости α=0,01

—средняя зарплата сотрудников меньше рекламируемой, а разброс в зарплатах больше на всех уровнях значимости

 

Предполагается, что месячная зарплата сотрудников фирмы составляет 600 $ при стандартном отклонении σ = 100 $. Выборка из 49 человек дала следующие результаты: 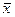= 500$ и S = 120$. На основании результатов проведенных наблюдений можно утверждать, что:

+ средняя зарплата сотрудников меньше рекламируемой на всех уровнях значимости, а разброс в зарплатах больше на уровне значимости α=0,05 и α=0,1

—средняя зарплата сотрудников меньше рекламируемой на всех уровнях значимости, а разброс в зарплатах больше только на уровне значимости α=0,01

—средняя зарплата сотрудников меньше рекламируемой, а разброс в зарплатах больше на всех уровнях значимости

 

Предполагается, что месячная зарплата сотрудников фирмы составляет 800 $ при стандартном отклонении σ = 40 $. Выборка из 49 человек дала следующие результаты: 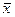= 780$ и S = 50$. На основании результатов проведенных наблюдений можно утверждать, что:

средняя зарплата сотрудников меньше рекламируемой, а разброс в зарплатах больше на всех уровнях значимости

—средняя зарплата сотрудников меньше рекламируемой на всех уровнях значимости, а разброс в зарплатах больше на уровне значимости α=0,05 и α=0,01

—средняя зарплата сотрудников меньше рекламируемой на всех уровнях значимости, а разброс в зарплатах больше на уровне значимости α=0,1

 

Имеется три вида акций A, B и C каждая стоимостью 20 у.е., дивиденды по которым являются независимыми СВ со средним значением 8 % и дисперсией 25. Формируются два портфеля инвестиций. Портфель z₁ состоит из 60 акций A. Портфель z₂ включает в себя по 20 акций A, B и C. Коэффициент корреляции между дивидендами по акциям A и C равен -0,5, но обе величины не коррелируют с дивидендами по акциям B. Рассчитать риски от вложений средств в данные портфели инвестиций:

+ z₁=90000; z₂=20000

—z₁=90000; z₂=29975

—z₁=90000; z₂=1475

—z₁=1500; z₂=1525

 

Имеется три вида акций A, B и C, каждая стоимостью 15 у.е., дивиденды по которым являются независимыми СВ со средним значением 7 % и дисперсией 16. Формируются два портфеля инвестиций. Портфель z₁ состоит из 100 акций A. Портфель z₂ включает в себя 40 акций A, 40 акций B и 20 акций C. Коэффициент корреляции между дивидендами по акциям A и B равен -0,6, но обе величины не коррелируют с дивидендами по акциям C. Рассчитать риски от вложений средств в данные портфели инвестиций:

—z₁=160000; z₂=57580,8

—z₁=160000; z₂=57600

—z₁=1600; z₂=1580,8

+ z₁=160000; z₂=26880

 

Парная регрессия (Задачи)

 

Зависимость спроса на кухонные комбайны y от цены x по 12 торговым точкам компании имеет вид:

В скобках – фактическое значение t – критерия. Ранее предполагалось, что увеличение цены на 1 % приводит к уменьшению спроса на 1,4 %. Можно ли утверждать, что приведенное уравнение регрессии подтверждает это предположение?

+Нет, на любом уровне (0,1; 0,05 и 0,01)

—Да, на любом уровне (0,1; 0,05 и 0,01)

—Нет, только на уровнях 0,05 и 0,1

—Нет, только на уровне 0,1

 

Зависимость спроса на кухонные комбайны y от цены x по 18 торговым точкам компании имеет вид:

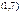
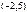
В скобках – фактическое значение t – критерия. Ранее предполагалось, что увеличение цены на 1 % приводит к уменьшению спроса на 1,5 %. Можно ли утверждать, что приведенное уравнение регрессии подтверждает это предположение?