—Нет, на любом уровне (0,01, 0,05 и 0,1)
—Да, только на уровнях 0,01 и 0,05
—Да, на любом уровне (0,1, 0,05 и 0,01)
Для двух видов продукции А и Б зависимость удельных постоянных расходов от объема выпускаемой продукции выглядят следующим образом:

Сравнить эластичности затрат по каждому виду продукции при x=50 и определить объем выпускаемой продукции обоих видов, при котором их эластичность будут одинаковы.
+ 



— 

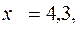

— 



— 



Для двух видов продукции А и Б зависимость удельных постоянных расходов от объема выпускаемой продукции выглядят следующим образом:

Сравнить эластичности затрат по каждому виду продукции при x=60 и определить объем выпускаемой продукции обоих видов, при котором их эластичность будут одинаковы.
+ 

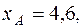

— 


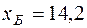
— 

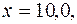
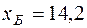
— 

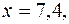

Для двух видов продукции А и Б зависимость удельных постоянных расходов от объема выпускаемой продукции выглядят следующим образом:

Сравнить эластичности затрат по каждому виду продукции при x=80 и определить объем выпускаемой продукции обоих видов, при котором их эластичность будут одинаковы.
+ 



— 



— 



— 



Для двух видов продукции А и Б зависимость удельных постоянных расходов от объема выпускаемой продукции выглядят следующим образом:

Сравнить эластичности затрат по каждому виду продукции при x=40 и определить объем выпускаемой продукции обоих видов, при котором их эластичность будут одинаковы
+ 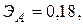

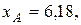

— 



— 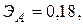



— 



Для двух видов продукции А и Б зависимость удельных постоянных расходов от объема выпускаемой продукции выглядят следующим образом:

Сравнить эластичности затрат по каждому виду продукции при x=25 и определить объем выпускаемой продукции обоих видов, при котором их эластичность будут одинаковы
+ 



— 



— 



— 



Для двух видов продукции А и Б зависимость удельных постоянных расходов от объема выпускаемой продукции выглядят следующим образом:

Сравнить эластичности затрат по каждому виду продукции при x=30 и определить объем выпускаемой продукции обоих видов, при котором их эластичность будут одинаковы.
+ 



— 
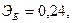


— 



— 



Для двух видов продукции А и Б зависимость удельных постоянных расходов от объема выпускаемой продукции выглядят следующим образом:
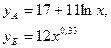
Сравнить эластичности затрат по каждому виду продукции при x=40 и определить объем выпускаемой продукции обоих видов, при котором их эластичность будут одинаковы
+ 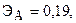



— 



— 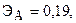

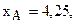
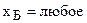
— 



Для двух видов продукции А и Б зависимость удельных постоянных расходов от объема выпускаемой продукции выглядят следующим образом:

Сравнить эластичности затрат по каждому виду продукции при x=45 и определить объем выпускаемой продукции обоих видов, при котором их эластичность будут одинаковы.
+ 



— 

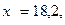

— 


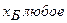
— 



Для двух видов продукции А и Б зависимость удельных постоянных расходов от объема выпускаемой продукции выглядят следующим образом:

Сравнить эластичности затрат по каждому виду продукции при x=40 и определить объем выпускаемой продукции обоих видов, при котором их эластичность будут одинаковы.
— 



— 



— 



+ 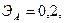



Для двух видов продукции А и Б зависимость удельных постоянных расходов от объема выпускаемой продукции выглядят следующим образом:
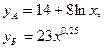
Сравнить эластичности затрат по каждому виду продукции при x=55 и определить объем выпускаемой продукции обоих видов, при котором их эластичность будут одинаковы.
+ 

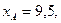

— 


— 



— 



Пусть имеется уравнение парной регрессии:
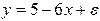 ,
,
построенное по 15 наблюдениям. При этом r= - 0,7. Доверительный интервал для коэффициента регрессии в этой модели имеет вид:
С вероятностью 0,99
— (-9,67;-2,33) с вероятностью 0,99
— (-9,01; -2,99) с вероятностью 0,95
— (-8,53; -2,32) с вероятностью 0,9
Пусть имеется уравнение парной регрессии:
 ,
,
построенное по 18 наблюдениям. При этом  . Доверительный интервал для коэффициента регрессии в этой модели имеет вид:
. Доверительный интервал для коэффициента регрессии в этой модели имеет вид:
С вероятностью 0,9
— (-6,92;-3,08) с вероятностью 0,95
— (-8,22; -1,78) с вероятностью 0,95
— (-7,34; -2,66) с вероятностью 0,99
Пусть имеется уравнение парной регрессии:
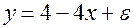 ,
,
построенное по 20 наблюдениям. При этом  . Доверительный интервал для коэффициента регрессии в этой модели имеет вид:
. Доверительный интервал для коэффициента регрессии в этой модели имеет вид:
С вероятностью 0,95
— (-5,91;-2,09) с вероятностью 0,99
— (-6,32; -1,68) с вероятностью 0,99
— (-5,91; -2,09) с вероятностью 0,95
Пусть имеется уравнение парной регрессии:
 ,
,
построенное по 22 наблюдениям. При этом  . Доверительный интервал для коэффициента регрессии в этой модели имеет вид:
. Доверительный интервал для коэффициента регрессии в этой модели имеет вид:
С вероятностью 0,95
— (-0,49;6,49) с вероятностью 0,95
— (-1,76; 7,76) с вероятностью 0,99
— (1,23; 4,77) с вероятностью 0,99
Пусть имеется уравнение парной регрессии:
 ,
,
построенное по 24 наблюдениям. При этом  . Доверительный интервал для коэффициента регрессии в этой модели имеет вид:
. Доверительный интервал для коэффициента регрессии в этой модели имеет вид:
С вероятностью 0,99
— (2,50; 11,50) с вероятностью 0,99
— (6,36; 7,64) с вероятностью 0,90
— (3,68; 10,32) с вероятностью 0,95
Пусть имеется уравнение парной регрессии:
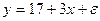 ,
,
построенное по 20 наблюдениям. При этом  . Доверительный интервал для коэффициента регрессии в этой модели имеет вид:
. Доверительный интервал для коэффициента регрессии в этой модели имеет вид:
С вероятностью 0,90
— (2,14;3,86) с вероятностью 0,95
— (2,28; 3,72) с вероятностью 0,99
— (1,85; 4,15) с вероятностью 0,99
Пусть имеется уравнение парной регрессии:
 ,
,
построенное по 15 наблюдениям. При этом  . Доверительный интервал для коэффициента регрессии в этой модели имеет вид:
. Доверительный интервал для коэффициента регрессии в этой модели имеет вид:
С вероятностью 0,95
— (0,05;9,95) с вероятностью 0,99
— (1,17; 8,83) с вероятностью 0,90
— (0,35; 9,65) с вероятностью 0,95
Пусть имеется уравнение парной регрессии:
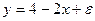 ,
,
построенное по 18 наблюдениям. При этом  . Доверительный интервал для коэффициента регрессии в этой модели имеет вид:
. Доверительный интервал для коэффициента регрессии в этой модели имеет вид:
С вероятностью 0,95
— (-3,7;-0,3) с вероятностью 0,99
— (-3,21; -0,79) с вероятностью 0,90
— (-3,56; -0,44) с вероятностью 0,95
Пусть имеется уравнение парной регрессии:
 ,
,
построенное по 16 наблюдениям. При этом 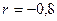 . Доверительный интервал для коэффициента регрессии в этой модели имеет вид:
. Доверительный интервал для коэффициента регрессии в этой модели имеет вид:
С вероятностью 0,99
— (-4,36;-1,64) с вероятностью 0,95
— (-3,98; -2,02) с вероятностью 0,90
— (-4,96; -1,04) с вероятностью 0,99
Пусть имеется уравнение парной регрессии:
 ,
,
построенное по 14 наблюдениям. При этом  . Доверительный интервал для коэффициента регрессии в этой модели имеет вид:
. Доверительный интервал для коэффициента регрессии в этой модели имеет вид:
С вероятностью 0,95
— (-17,32; 1,32) с вероятностью 0,99
— (-16,13; 0,13) с вероятностью 0,90
— (-15,76; -0,24) с вероятностью 0,90
Уравнение регрессии потребления материалов y от объема производства x, построенное по 15 наблюдениям, имеет вид:



В скобках – фактическое значение t – критерия. Коэффициент детерминации для этого уравнения равен:
+0,552
—0,575
—0,439
—0,648
Уравнение регрессии потребления материалов y от объема производства x, построенное по 18 наблюдениям, имеет вид:



В скобках – фактическое значение t – критерия. Коэффициент детерминации для этого уравнения равен:
+0,360
—0,384
—0,247
—0,456
Уравнение регрессии потребления материалов y от объема производства x, построенное по 20 наблюдениям, имеет вид:


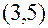
В скобках – фактическое значение t – критерия. Коэффициент детерминации для этого уравнения равен:
+0,405
—0,428
—0,292
—0,501
Уравнение регрессии потребления материалов y от объема производства x, построенное по 15 наблюдениям, имеет вид:



В скобках – фактическое значение t – критерия. Коэффициент детерминации для этого уравнения равен:
+0,448
—0,564
—0,356
—0,621
Уравнение регрессии потребления материалов y от объема производства x, построенное по 20 наблюдениям, имеет вид:



В скобках – фактическое значение t – критерия. Коэффициент детерминации для этого уравнения равен:
+0,491
—0,425
—0,379
—0,531
Уравнение регрессии потребления материалов y от объема производства x, построенное по 18 наблюдениям, имеет вид:

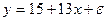

В скобках – фактическое значение t – критерия. Коэффициент детерминации для этого уравнения равен:
+0,327
—0,425
—0,517
—0,369
Уравнение регрессии потребления материалов y от объема производства x, построенное по 25 наблюдениям, имеет вид:



В скобках – фактическое значение t – критерия. Коэффициент детерминации для этого уравнения равен:
+0,373
—0,321
—0,415
—0,512
Уравнение регрессии потребления материалов y от объема производства x, построенное по 15 наблюдениям, имеет вид:



В скобках – фактическое значение t – критерия. Коэффициент детерминации для этого уравнения равен:
+0,675
—0,519
—0,631
—0,620
Уравнение регрессии потребления материалов y от объема производства x, построенное по 18 наблюдениям, имеет вид:



В скобках – фактическое значение t – критерия. Коэффициент детерминации для этого уравнения равен:
+0,461
—0,395
—0,423
—0,522
Уравнение регрессии потребления материалов y от объема производства x, построенное по 20 наблюдениям, имеет вид:



В скобках – фактическое значение t – критерия. Коэффициент детерминации для этого уравнения равен:
+0,495
—0,517
—0,444
—0,396
Уравнение регрессии имеет вид: ln y = 4,5 + 0,003x + ln e. При значении фактора, равном 85, коэффициент эластичности y по х составит:
+0,255
—0,003
—0,00066
—0,0536
—0,00063
Уравнение регрессии имеет вид: ln y = 4,5 + 0,003 ln x + ln e. При значении фактора, равном 85, коэффициент эластичности y по х составит:
+0,003
—0,255
—0,00066
—0,0536
—0,00071
Уравнение регрессии имеет вид: y = 4,5 + 0,003 ln x + e. При значении фактора, равном 85, коэффициент эластичности y по х составит:
+0,00066
—0,255
—0,003
—0,0536
—0,00063
Уравнение регрессии имеет вид: y = 4,5 + 0,003x + e. При значении фактора, равном 85, коэффициент эластичности y по х составит:
+0,0536
—0,255
—0,003
—0,00063
—0,0582
Уравнение регрессии имеет вид: ln y = 2,3 + 0,0043x + ln e. При значении фактора, равном 108, коэффициент эластичности y по х составит:
+0,4644
—0,0043
—0,00185
—0,168
—0,4218
Уравнение регрессии имеет вид: ln y = 2,3 + 0,0043 ln x + ln e. При значении фактора, равном 108, коэффициент эластичности y по х составит:
+0,0043
—0,4644
—0,00185
—0,168
—0,00129
Уравнение регрессии имеет вид: y = 2,3 + 0,0043 ln x + e. При значении фактора, равном 108, коэффициент эластичности y по х составит:
+0,00185
—0,0043
—0,4644
—0,168
—0,4215
Уравнение регрессии имеет вид: y = 2,3 + 0,0043x + e. При значении фактора, равном 108, коэффициент эластичности y по х составит:
+0,168
—0,00185
—0,0043
—0,4644
—0,00129
Уравнение регрессии имеет вид: ln y = 2,2 + 0,0037x + ln e. При значении фактора, равном 95, коэффициент эластичности y по х составит:
+0,3515
—0,0037
—0,00167
—0,137
—0,167
Уравнение регрессии имеет вид: ln y = 2,2 + 0,0037 ln x + ln e. При значении фактора, равном 95, коэффициент эластичности y по х составит:
+0,0037
—0,3515
—0,00167
—0,137
—0,4644
Уравнение регрессии имеет вид: y = 2,2 + 0,0037 ln x + e. При значении фактора, равном 95, коэффициент эластичности y по х составит:
+0,00167
—0,0037
—0,3515
—0,137
—0,00137
Уравнение регрессии имеет вид: y = 2,2 + 0,0037x + e. При значении фактора, равном 95, коэффициент эластичности y по х составит:
+0,137
—0,00167
—0,0037
—0,3515
—0,3218
Уравнение регрессии имеет вид: ln y = 1,8 + 0,0027x + ln e. При значении фактора, равном 125, коэффициент эластичности y по х составит:
+0,3375
—0,0015
—0,0027
—0,158
—0,3916
Уравнение регрессии имеет вид: ln y = 1,8 + 0,0027 ln x + ln e. При значении фактора, равном 125, коэффициент эластичности y по х составит:
+0,0027
—0,3375
—0,0015
—0,158
—0,00158
Уравнение регрессии имеет вид: y = 1,8 + 0,0027 ln x + e. При значении фактора, равном 125, коэффициент эластичности y по х составит:
+0,0015
—0,0027
—0,3375
—0,158
—0,00158
Уравнение регрессии имеет вид: y = 1,8 + 0,0027x + e. При значении фактора, равном 125, коэффициент эластичности y по х составит:
+0,158
—0,0015
—0,0027
—0,3375
—0,4218
Множественная регрессия (Задачи)
Уравнение регрессии в стандартизированном виде имеет вид:


Частные коэффициенты эластичности равны:
+0,266; -0,246; 0,258
—0,266; -0,258; 0,246
—0,258;-0,266; 0,263
—0,258; -0,246; 0,266
Уравнение регрессии в стандартизированном виде имеет вид:


Частные коэффициенты эластичности равны:
+-1,163; 0,736; -0,889
—-1,163; 0,889; -0,736
—-0,736; 1,163; -0,889
—-0,889; 1,163; -0,736
Стандартизованное уравнение регрессии имеет вид:


Частные коэффициенты эластичности равны:
+0,827; -0,607; -1,005
—0,827; -0,563; -0,923
—1,005; -0,607; -0,827
—0,827; -1,005; -0,607
Стандартизованное уравнение регрессии имеет вид:


Частные коэффициенты эластичности равны:
+0,23; -0,428; 0,476
—0,32; -0,476; 0,428
—0,23; -0,478; 0,428
—0,372; -0,32; 0,476
Стандартизованное уравнение регрессии имеет вид:


Частные коэффициенты эластичности равны:
+0,728; -1,213; 0,376
—0,728; -0,376; 1,213
—1,213; -0,728; 0,376
—1,213; -0,728; 0,436
Стандартизованное уравнение регрессии имеет вид:

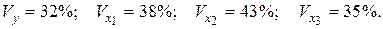
Частные коэффициенты эластичности равны:
+0,438; 0,558; -0,384
—0,438; 0,384; -0,558
—0,558; -0,438; 0,384
—0,558; 0,732; -0,461
Стандартизованное уравнение регрессии имеет вид:


Частные коэффициенты эластичности равны:
+0,327; -0,23; 0,493
—0,327; -0,493; 0,552
—0,493; -0,327; 0,552
—0,493; -0,23; 0,327
По 18 наблюдениям получены следующие данные:

 ;
;  ;
;  ;
;  ;
;  .
.
Значения скорректированного коэффициента детерминации, частных коэффициентов эластичности и параметра  равны:
равны:
+0,575; 0,57; -0,55; 3,47; -174,45
—0,575; 0,55; -0,57; 3,47; 174,45
—0,603; 0,57; -0,55; 3,47; -174,45
—0,603; 0,55; -0,57; 2,17; 278,7
По 17 наблюдениям получены следующие данные:

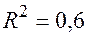 ;
;  ;
;  ;
;  ;
;  .
.
Значения скорректированного коэффициента детерминации, частных коэффициентов эластичности и параметра  равны:
равны:
+0,508; 0,43; 0,62; -5,63; 278,7
—0,508; 0,62; 0,43; -5,63; -278,7
—0,543; 0,43; 0,62; -5,63; -278,7
—0,543; 0,43; 0,62; -5,15; 278,7
По 22 наблюдениям получены следующие данные:

 ;
;  ;
;  ;
;  ;
; 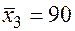 .
.
Значения скорректированного коэффициента детерминации, частных коэффициентов эластичности и параметра  равны:
равны:
+0,627; 4,73; -1,1; -4,1; 58,6
—0,627; 4,1; -1,1; 4,73; 58,6
—0,646; 4,73; -1,1; -4,1; -58,6
—0,646; 4,1; -1,1; -5,2; 58,6
По 25 наблюдениям получены следующие данные:

 ;
;  ;
;  ;
;  ;
;  .
.
Значения скорректированного коэффициента детерминации, частных коэффициентов эластичности и параметра  равны:
равны:
+0,429; -1,73; -0,33; 0,3; 220,2
—0,429; -1,73; -0,3; 0,33; -220,2
—0,455; 1,73; 0,33; 0,3; 220,2
—0,455; -1,73; -0,3; 0,33; -220,2
По 24 наблюдениям получены следующие данные:

 ;
;  ;
;  ;
;  ;
;  .
.
Значения скорректированного коэффициента детерминации, частных коэффициентов эластичности и параметра 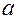 равны:
равны:
+0,517; 0,06; 0,37; -1,52; 313,0
—0,517; 0,36; 0,07; -0,84; 313,0
—0,54; 0,37; 0,06; -1,52; -313,0
—0,54; 0,06; 0,37; -1,52; -313,0
По 28 наблюдениям получены следующие данные:

 ;
;  ;
;  ;
;  ;
;  .
.
Значения скорректированного коэффициента детерминации, частных коэффициентов эластичности и параметра  равны:
равны:
+0,685; -0,26; -0,25; -0,96; 297,1
—0,686; -0,25; -0,26; -0,96; -297,1
—0,698; -0,26; -0,25; -0,96; -297,1
—0,698; -0,96; -0,25; -0,26; 297,1
По 26 наблюдениям получены следующие данные:

 ;
;  ;
;  ;
;  ;
;  .
.
Значения скорректированного коэффициента детерминации, частных коэффициентов эластичности и параметра  равны:
равны:
+0,568; 3,16; -1,22; -2,78; 146,5
—0,568; 3,16; -1,22; -2,56; -146,5
—0,587; 3,16; -1,22; -2,78; 146,5
—0,587; 3,16; -1,22; -2,78; -146,5
В уравнении регрессии: 

Восстановить пропущенные характеристики; построить доверительный интервал для
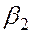 с вероятностью 0,95, если n = 12
с вероятностью 0,95, если n = 12
+ 

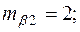 (-12,02; -2,98)
(-12,02; -2,98)
— 

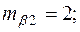 (-12,02; -2,98)
(-12,02; -2,98)
— 

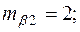 (-11,12; -3,88)
(-11,12; -3,88)
— 

 (-11,12; -3,88)
(-11,12; -3,88)
Уравнение регрессии в стандартизованном виде имеет вид:
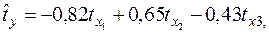

Как влияют факторы на результат и каковы значения частных коэффициентов эластичности?
+Наибольшее влияние на результат оказывает фактор  , наименьшее
, наименьшее 



—Наибольшее влияние на результат оказывает фактор  наименьшее -
наименьшее - 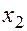 ;
; 

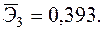
—Наибольшее влияние на результат оказывает фактор  наименьшее -
наименьшее - 

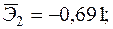

—Наибольшее влияние на результат оказывает фактор  наименьшее -
наименьшее - 



Уравнение регрессии в стандартизованном виде имеет вид:


Как влияют факторы на результат и каковы значения частных коэффициентов эластичности?
+Наибольшее влияние на результат оказывает фактор 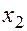 , наименьшее
, наименьшее 



—Наибольшее влияние на результат оказывает фактор  наименьшее -
наименьшее - 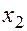 ;
; 


—Наибольшее влияние на результат оказывает фактор  наименьшее -
наименьшее - 



—Наибольшее влияние на результат оказывает фактор  наименьшее -
наименьшее - 



Уравнение регрессии в стандартизованном виде имеет вид:


Как влияют факторы на результат и каковы значения частных коэффициентов эластичности?
+Наибольшее влияние на результат оказывает фактор  , наименьшее
, наименьшее 



—Наибольшее влияние на результат оказывает фактор  наименьшее -
наименьшее -  ;
; 


—Наибольшее влияние на результат оказывает фактор  наименьшее -
наименьшее - 



—Наибольшее влияние на результат оказывает фактор  наименьшее -
наименьшее - 
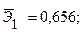

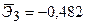
По 20 наблюдениям получены следующие данные:

Значения скорректированного коэффициента детерминации, частных коэффициентов эластичности и параметра  равны:
равны:
+ 
— 
— 
— 
По 16 наблюдениям получены следующие данные:
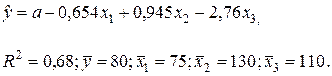
Значения скорректированного коэффициента детерминации, частных коэффициентов эластичности и параметра  равны:
равны:
+ 
— 
— 
— 









Уравнения регрессии y на 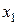 и
и  в стандартизованном и натуральном масштабе имеют вид:
в стандартизованном и натуральном масштабе имеют вид:
+ 

— 

— 

— 

. 








Уравнения регрессии  на
на 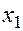 и
и 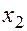 в стандартизованном и натуральном масштабе имеют вид:
в стандартизованном и натуральном масштабе имеют вид:
+ 

— 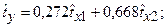

— 

— 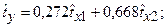

 ;
;
 .
.
Уравнения регрессии в стандартизированном и натуральном масштабе имеют вид:
+ 
— 
— 
— 

 .
.
Уравнения регрессии в стандартизированном и натуральном масштабе имеют вид:
+ 
— 
— 
— 

 .
.
Уравнения регрессии в стандартизированном и натуральном масштабе имеют вид:
+ 
— 
— 
— 

 .
.
Уравнения регрессии в стандартизированном и натуральном масштабе имеют вид:
+ 
— 
— 
— 
При построении регрессионной зависимости некоторого результативного признака на 8 факторов по 25 измерениям коэффициент детерминации составил 0,736. После исключения 3 факторов коэффициент детерминации уменьшился до 0,584. Обоснованно ли было принятое решение на уровнях значимости 0,1, 0,05 и 0,01:






