Запасы – товары материальной ценности, ожидающие личного или производст. постребления.
- Это форма сущ-я матер потока в опред время и опред месте.
Операц-е запасы создаются в связи с произв-й необх-ю, страховые- для защиты от неконтролируемого поведения покупателей и поставщиков, спекулятивные – когда компания прогнозирует рост цен на ресурсы.
Запасы: операционные (с производ необходимостью), страховые, спекулятивные (созд-ся, когда п/п прогнозир увел цен)
Факторы, способствующие увеличению запасов:
1) низкое качество поставляемых товаров
2) неточности в прогнозировании
3) низкое качество производства
4) большие расстояния
5) низкая надежности поставки
6) экономия на скидках
Затраты на содержание запасов:
1). капитальные замапы – стоимость в запасах капитала (упущенная выгода)
2). затраты, связ с хранением
3). страх-е запасов
4). затраты в связи с износом и порчей запасов
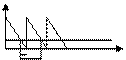
Осн. модель упр-ния запасами с фиксиров размером запаса.
Цель – оптимизация размера q, чтобы общие издержки были min.
С- цена ед товара
S – организ издержки на 1 партию товара все зав-ти от размера партии
D – годовая потребность в товаре
H – издержки на хранение ед товара в год
Q – размер партии поставки
Где S,D,H – известны.
Составим функцию общих издержек, которая сост из 3 частей:
1). C*D – общ ст-ть товара в год
2). D/q кол-во поставок
S*D/Q – общ орг издержки за год
3). Q/2*H – издержки на хранение в год
C(Q) = C*D+(D/Q)*S+(Q/2)*H
Нужно взять производную для нахождения min ф-ии и прировнять ее к 0.
C’(Q) = -(D*S)/Q² + H/2=0
H/2 = ds/q²
Q*= √(2*S*D)/H – оптимальный размер заказа.
n*=d/q* - оптимальное число поставок за год
t*= 365/n* - цикл пополнения запаса t* (время м/у заказами).
В этой модели упр-ния запасами одно существенное допущение
График
 |
Q*
ROP
 |
Тетта 3п T* t
--- говорит о том, что запасы пополняются мгновенно
Определение момента заказа
ROP=λ*ίзп
λ- интенсивность спроса.
ίзп- время запаздывания поставок(соотв-т времени выполнения заказа).
λ=d/52недели
ίзп соотв-т вр-ни выполнения цикла заказа
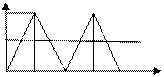
Модель производственных поставок (модификация 1-й модели)
Р – производ-ть произв-й линии (р ед. в год)
В начале цикла происх подключение к производ линии, кот продолж-ся до пополнения Q единиц, после пополнения запасов не происходит до тех пор, пока не возникнет дефицит.
Схема
M
M/2
Ф-ия c(q) состоит из 3х частей
1.C*d – общ стоимость товара в год
2. (d/q)*S
3. тетта – время поставки. В течение этого времени происходит как пополнение с интенсивностью р, так и расходование с интенсивностью d запасов. Увел-е запаса происх со скоростью (p-d)
M=(p-d)* ί =max возм запас
M<q т.к. q=p*ί => ί=q/p
M=(p-d)*(q/p)
Средний размер (поэтому делим на 2)
M/2 =(p-d)*q /2p
=> [(p-d)*q /2p] *h – изд-и на хранение в этой модели.
C(q) = cd + (d/q)*s + [(p-d)*q /2p] *h.
Берем производную:
С’(q)= -(d/q²)*S + (p-d)h /2p = 0
q*= √2sdp/ h(p-d)
Модель поставок со скидкой.
Если размер Q не менее заданного Qo (задано), то поставщик предлагает скидку и новая цена Co<C (С – прежняя цена).
Ф-ция общих издержек в точке q=qo:
C*D+(D/Q)*S+(Q/2)*h, если Q<Qo
C(q) =
CoD+(D/Q)*S+(Q/2)*h, если Q≥Qo
Обе ф-ии f(q) и fo(q) имеют min в точке f’(q)=f’(qo), т.е. в точке qср.=√2sd/h
Для принятия решения какой размер партии оптимален, следует сравнить значения C(q) в точках Qo и Qср.
Там, где значение меньше, там будет оптим, т.е. q*=qo либо q*=qср.
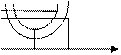
График:
C(qср.)
С(q0)
Qср. Q0
С(qo)<C(qср). Выгоднее работать с партией со скидкой.
График
С(q0) 
C(qср.)
Qср. Q0
C(q(−))<C(qo) выгодно работать с оптимальн размерами.
Модель упр-ния запасами с фиксиров интервалами м/у заказами.
Осн. хар-р – интервал рассчитывается на осн-и I = N:d/q* → I = Nq*/d
N- число дней в году, d- годовой запас
РЗ=МЖЗ-ТЗ+ОП, где РЗ- размер заказа, МЖЗ – мах желат заказ, ТЗ-текущ заказ, ОП-ожид потребеление до момента поставки
Модель подходит для запасов со след хар-ми:
-малоценные предметы
-низк ст-ть хранения
-низк издержки, даже если запасы законч
-один из многих предметов заказ-х у одного пост-ка
-скидка с цены зависит от ст-ти заказа сразу по неск позициям
-расход материала
График
Объем МЖЗ
запасов
страховой
запас
tпост Tпост. Время задержки поставки
Плюсы и минусы двух моделей: Модель произ-х поставок «+»: МЖЗ меньше, умен изд-ки на хранение, «-»: пост контроль наличия запасов, Модель упр-я запасами с фиксир интервалом «+»: контроль не нужен, «-»: МЖЗ больше, растут изд-ки на хранение.
Модель упр-ния запасами с установленной периодичностью пополнения запаса до постоянного уровня.
(модификация двух предыдущих моделей, она наиболее устойчива к колебаниям спроса)
Чтобы предотвратить завышение запасов на складе, а также их дефицит, заказы произ-ся не только в установл время, но и по достижению запасов фиксир порогового уровня.
Заказы подразделяются на 2 категории:
1). Плановые (через фиксир интервал времени)
2). Внеплановые (когда запасы достигли некоего порога)
Схема:
Модель упр-я запасами по min/max и с постоян периодичностью пополнения запаса.
(модификация 1 и 2 модели)
Эта система содержит в себе эл-ты упр-ния запасами основных систем. Разработана для усл. высокой стоимости оформленного заказа, допустимости дефицита и крайней нежелательности создания чрезмерных запасов.
РЗ=МЖЗ-q, где q – прогнозируемый размер запаса на момент поставки. Система работает с 2 уровнями: max и min.
Заказы произ-ся при усл-и, что запасы на складе оказались меньшим или равными установл миним уровня, а поставка пополняет запасы до мах желательного уровня.
Упр-е запасами с помощью ABC и XYZ распределениями.
1) ABC- анализ связан со стоимостью.
График
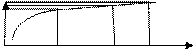100% В С
95%
80% А
20% 30% 50%
А – 20% дорогостоящ товаров, ежегод контроль (модель III и I).
В – со средней ценой 30% (от общ кол-ва). Контроль 1раз в месяц (модель I и II).
С – недорогой. 50%. Контроль 1 раз в квартал (IV и II модели).
Х – кол-во номенклатур позиций
У – ст-ть запасов нарастающ итогом.
Вклад общий А=80% В=15% С=5%
50-100%
На 1т прих-ся 2%.
При упр-и запасами необх-мо учит-ть хар-р потребления запасов, а также точность прогноз-я изменения их потребности.
Для этого исп-ся XYZ анализ:
X – стабильная вел-на потребления и высок точностью прогноз-я срока их потребления
Y – известные тенденции и сред точностью прогноз-я измен потребности
Z – исп не регулярно, величину потребления прогнозировать сложно.
Для отнесения к XYZ расч-я коэф-т вариации спроса.
Если 0≤ν≤10% => x
10%≤ν≤25% => y
25%≤ν≤ бесконеч => z
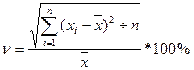
Xi – i значение спроса по i позиции, х ср. – среднее значение за период
Можно соединить АВС и ХУZ – получится 9 категорий товаров
| A | B | C | |
| X | AX | BX | CX |
| Y | AY | BY | CY |
| Z | AZ | BZ | Z |
Категории СХ, СУ, СZ на практике упр-ния одинаково, обычно планирование таких товаров происходит на год с ежемесячной проверкой их наличия на складе.
Для категорий ВХ, ВУ, ВZ совпадают сроки планирования, но различаются по способам доставки, по размерам.
Для категорий АХ, АУ, АZ строится индив-й план упр-ния.
