Построение графика суммарной работы

Методом графического интегрирования графика момента сил сопротивления был построен график работы сил сопротивления (с отрезоком интегрирования k=30 мм) . Приведенный момент движущих сил (φ₁)= const определили из условия, что при установившемся режиме |А^дв|=|А^с| за цикл. Тогда, М_дв=173,8 Н^.м

Строим график (φ₁). Сложив ординаты графика момента движущего и момента сил сопротивления 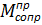, получили график приведенного суммарного момента .

Используя тот же метод графического интегрирования графика момента приведенного суммарного , получили график работы суммарной .

Расчет масштаба графика работы приведенной суммарной:

, где

- масштаб угла поворота , мм/рад;

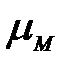- масштаб момента , мм/Н^.м,

K - отрезок интегрирования, мм.

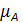= 0, 16 мм/Дж.

 

Построение графика приведенного момента суммарного II группы звеньев.

Для построения графика приведенного суммарного момента II группы звеньев воспользовалисьметодом приведения масс. В основу метода приведения масс положено условие равенст­ва кинетической энергии всех звеньев механизма и звена дина­мической модели. В этом случае закон движения последнего будет таким же, как и закон движения начального звена реального ме­ханизма.

Для определения приведенного момента инерции 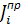каждого звена механизма составили равенство кинетических энергий рассматриваемого звена и звена модели.

В зависимости от характера движения звена существуют сле­дующие варианты равенстве кинетических энергий:

При поступательном движении i-го звена механизма

, откуда

При вращательном движении звена вокруг неподвижной оси

,

откуда

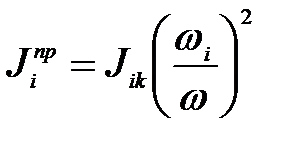
При плоскопараллельном движении звена

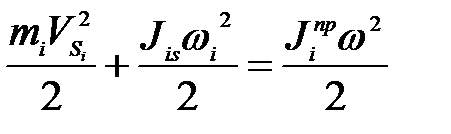
откуда

где 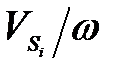, - передаточные функции.

Суммарный приведенный момент инерции всего механизма ра­вен сумме приведенных моментов инерции всех его звеньев и за­висит от положения механизма:

, где

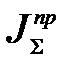зависит от отношения скоростей и может определять­ся без учета действительного закона движения звеньев.

 

Приведенный момент инерции звена 3 находится по формуле

 

J₃^пр= m_3*(V_C/ω₁)²

 

Заменяя и переходя к отрезкам, взятым из плана возможных скоростей, получили

 

J₃^пр= m₃ ^* l²_AB ^*(V_C/V_B)²

 

Рассчитали для каждого из 12 положений с помощью программы Ar2u. Полученные данные приведены в таблице 2.6.

 

Таблица 2.6

	0,035501
	0,031966
	0,015871
	0,002771
	0,0007
	0,010583
	0,027158
	0,036627
	0,026233
	0,005764
	0,001507
	0,019249
	0,035501

 

 

Аналогично для звена 5

J₅^пр= m₅(V_D/ω₁)²= m₅ ^* l²_OB ^* (V_D/V_B)²

Полученные данные приведены в таблице 2.7.

Таблица 2.7

	0,005764
	0,001507
	0,019249
	0,035501
	0,031966
	0,015871
	0,002771
	0,0007
	0,010583
	0,027158
	0,036627
	0,026233
	0,005764

 

Приведенный момент инерции звена 2 определяли по формуле

Заменяя ω₂= V_CB/l_CB и переходя к отрезкам, получали

J₂^пр=J_2П^пр+ J_2В^пр= m₂^* l²_OB ^. (pS₂/pb)²+ J_2S^{. .} (l_OB/ l_BC)² (bc/pb)²

Полученные результаты для всех 12 положений приведены в таблице 2.8

 

Таблица 2.8

	0,000098	0,022986	0,023084
	0,000025	0,022722	0,022748
	0,000344	0,017569	0,017913
	0,000722	0,012652	0,013374
	0,00079	0,011822	0,012612
	0,000485	0,015653	0,016138
	0,000098	0,021317	0,021416
	0,000025	0,023654	0,02368
	0,000344	0,019642	0,019985
	0,000722	0,013251	0,013972
	0,00079	0,011984	0,012774
	0,000485	0,017386	0,017871
	0,000098	0,022986	0,023084

Аналогично для звена 4

Полученные результаты для всех 12 положений приведены в таблице 2.9

Таблица 2.9

	0,000722	0,013251	0,013972
	0,00079	0,011984	0,012774
	0,000485	0,017386	0,017871
	0,000098	0,022986	0,023084
	0,000025	0,022722	0,022748
	0,000344	0,017569	0,017913
	0,000722	0,012652	0,013374
	0,00079	0,011822	0,012612
	0,000485	0,015653	0,016138
	0,000098	0,021317	0,021416
	0,000025	0,023654	0,02368
	0,000344	0,019642	0,019985
	0,000722	0,013251	0,013972

 

Суммарный приведенный момент инерции всего механизма

Построив графики приведенных моментов инерции отдельных звень­ев масштабе , получили график сум­марного приведенного момента инерции . Данные для его построения приведены в таблице 1.10

 

Таблица 2.10

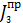
	0,023084	0,035501	0,013972	0,005764	0,078321
	0,022748	0,031966	0,012774	0,001507	0,068995
	0,017913	0,015871	0,017871	0,019249	0,070904
	0,013374	0,002771	0,023084	0,035501	0,07473
	0,012612	0,0007	0,022748	0,031966	0,068026
	0,016138	0,010583	0,017913	0,015871	0,060505
	0,021416	0,027158	0,013374	0,002771	0,064719
	0,02368	0,036627	0,012612	0,0007	0,073619
	0,019985	0,026233	0,016138	0,010583	0,072939
	0,013972	0,005764	0,021416	0,027158	0,048574
	0,012774	0,001507	0,02368	0,036627	0,074588
	0,017871	0,019249	0,019985	0,026233	0,083338
	0,023084	0,035501	0,013972	0,005764	0,078321