Метод наименьших квадратов

Сущность метода заключается в нахождении параметров модели, при которых минимизируется сумма квадратов отклонений эмпирических значений результативного признака от теоретических полученных по выбранному уравнению ргрессии.

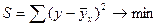
для линейной зависимости

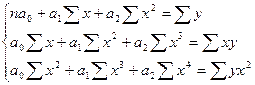для параболической зависимости

для гиперболической зависимости

Множественная регрессия

Изучение связи между тремя и более связанными между собой признаками носит название множественной (многофакторной) регрессии. При исследовании зависимостей методами множественной регрессии требуется определить аналитическое выражение связи между результативным признаков (Y) и множеством факторных признаков (x₁, x₂, x₃,…x_n).

Построение моделей множественной регрессии включает несколько этапов:

выбор формы связи (уравнения регрессии);

отбор факторных признаков;

обеспечение достаточного объема совокупности для получения реальных оценок.

Практика построения многофакторных моделей показывает, что все реально существующие зависимости между социально-экономическими явлениями можно описать, используя пять типов моделей:

линейная;

степенная;

показательная;

параболическая;

гиперболическая.

Качество уравнения регрессии зависит от степени достоверности и надежности исходных данных и объема совокупности.

Немаловажное значение имеет процедура отбора факторов в уравнение. Наиболее приемлемым способом отбора факторных признаков является шаговая регрессия. Сущность метода шаговой регрессии заключается в последовательном включении факторов в уравнение регрессии и последующей проверке их значимости.

Если при включении нового фактора в модель, коэффициенты регрессии меняют не только свои значения, но и знаки, а множественный коэффициент корреляции не возрастает, то данный факторный признак признается нецелесообразным для включения в модель связи.

Сложность и взаимно переплетение отдельных факторов, обуславливающих исследуемое экономическое явление, могу проявляться в так называемой мультиколлинеарности. Под мультиколлинеарностью понимается тесная зависимость между факторными признаками, включенными в модель. Одним из индикаторов определения мультиколлинеарности между признаками является превышение парным коэффициентом корреляции величины 0,8.

При наличии линейной связи между результативным и несколькими факторными признака, а также между парой факторных признаков определяется множественный коэффициент корреляции:

Множественный коэффициент корреляции изменяется в пределах от 0 до 1. Чем ближе R к единице свидетельствует о сильной зависимости между признаками.