Для выявления наличия связи, ее характера и направления используются методы приведения параллельных данных, аналитических группировок, графический, корреляции и регрессии.
Метод проведения параллельных данных основан на сопоставлении двух или нескольких рядов статистических величин. Данное сопоставление позоляет установить наличие связи и получить представление о ее характере.
Графический метод
Графическая взаимосвязь двух признаков изображается с помощью поля корреляции.
Корреляция – это статистическая зависимость между случайными величинами, не имеющими строго функционального характера, при которой изменение одной из случайных величин приводит к изменению математического ожидания другой.
Виды зависимостей:
1) парная корреляция – связь между двумя признаками (между двумя факторными либо между факторным и результативным признаком)
2) частная корреляция – зависимость между результативным и одним факторным признаком при фиксированном значении других факторных признаков
3) множественная корреляция – зависимость результативного и двух и более факторных признаков.
Корреляционный анализ имеет своей задачей количественное определение тесноты связи между двумя признаками.
Теснота связи количественно выражается величиной коэффициентов корреляции.
Теснота связи при линейной зависимости измеряется с помощью линейного коэффициента корреляции:

Линейный коэффициент корреляции изменяется в пределах от -1 до+1.
По степени тесноты связи различают количественные критерии оценки тесноты связи:
| Величина коэффициента корреляции | Характер связи |
| До ±0,3 | Практически отсутствует |
| ±0,3 – ±0,5 | Слабая |
| ±0,5 – ±0,7 | Умеренная |
| ±0,7 – ±1,0 | Сильная |
Теснота связи при криволинейной зависимости измеряется с помощью корреляционного отношения. Различают эмпирическое и теоретическое корреляционное отношение.
Эмпирическое корреляционное отношение: 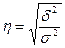
Регрессионный анализ заключается в определении аналитического выражения связи, в котором изменение одной величины обусловлено влиянием одной или нескольких независимых величин (факторов).
По форме зависимости различают:
- линейную регрессию, которая выражается уравнением прямой (линейной функции) вида: 
- нелинейную регрессию, которая выражается уравнениями вида:
парабола - 
гипербола -  и т.д.
и т.д.
По направлению связи различают:
А) прямую регрессию (положительную), возникающую при условии, если с увеличением или уменьшением независимой величины значения зависимой также соответственно увеличиваются или уменьшаются;
Б) обратную (отрицательную) регрессию, появляющуюся при условии, что с увеличением или уменьшением независимой величины зависимая соответственно уменьшается или увеличивается.
Парная регрессия
Парная регрессия характеризует связь между двумя признаками: результативным и факторным.
Оценка параметров уравнения регрессии а0, а1 осуществляется методом наименьших квадратов, в основе которого лежит предположение о независимости наблюдений исследуемой совокупности и нахождении параметров модели, при котором минимизируется сумма квадратов отклонений фактических значений результативного признака от теоретических, полученных по уравнению регрессии:

Система нормальных уравнений для нахождения параметров линейной парной регрессии методом наименьших квадратов имеет следующий вид:

где n – объем исследуемой совокупности (число единиц наблюдения).
В уравнениях регрессии параметр а0 показывает усредненное влияние на результативный признак неучтенных факторов; параметр а1 – коэффициент регрессии показывает, на сколько изменяется в среднем значение результативного признака при изменении факторного на единицу его собственного измерения.






