Зависимость от вида распределения и от способа отбора единиц совокупности по разному вычисляются характеристики параметров распределения.
| Характеристики параметров распределения | Генеральная совокупность | Выборочная совокупность |
| Объем выборки | N | n |
| Альтернативный признак | ||
| Численность единиц совокупности, обладающих признаком x | M | m |
| Доля единиц, обладающих изучаемым признаком x | 
| 
|
| Дисперсия |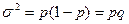 
| 
|
| Среднее квадратическое отклонение | 
| 
|
| Количественный признак | ||
| Среднее значение признака | 
| 
|
| Дисперсия | 
| 
|
| Среднее квадратическое отклонение | 
| 
|
Вследствие того, что выборочная совокупность отлична от генеральной, возникают ошибки выборки.
Два вида:
1) ошибки регистрации (могут быть случайными и систематическими)
2) ошибки репрезентативности (присущи только выборочному наблюдению).
Ошибка выборочного наблюдения – разность между величиной параметра генеральной совокупности и его величиной, вычисленной по результатам выборочного наблюдения.
Для среднего значения ошибки выборочного наблюдения
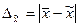- предельная ошибка выборки.
Предельная ошибка выборки зависит от способа отбора и процедуры выборки
Предельная ошибка выборки для некоторых способов
Формирования выборочной совокупности
 Метод отбора
| Повторный | Бесповторный | ||
| Вид выборки | Для средней | Для доли | Для средней | Для доли |
| Собственно-случайная и механическая | 
| 
| 
| 
|
| Типическая | 
| 
| 
| 
|
| Серийная |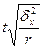 
| 
| 
| 
|
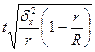
Средняя ошибка выборки выражает среднее квадратическое отклонение выборочной средней от генеральной средней
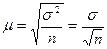
СОВ зависит:
1) от колеблемости признака в генеральной совокупности
2) от числа отобранных единиц.
СОВ показывает, какие возможны отклонения характеристик выборочной совокупности от соответствующих характеристик генеральной совокупности
О величине средней ошибки выборки судят с определенной вероятностью, на которую указывает коэффициент доверия (t)
Таким образом, зная выборочную среднюю и предельную ошибку выборки, можно определить пределы, в которых находится генеральная средняя
СОВ альтернативного признака определяется по формуле
; 
- доля выборочной совокупности
ПОВ альтернативного признака
Зная выборочную долю признака и предельную ошибку выборки, можно определить границы, в которых заключена генеральная доля
