Задача № 60.
Динамика продажи мясных консервов в РФ характеризуется следующими данными:
Годы 2000 2001 2002 2003 2004 2005 2006
Консервы 3223 4247 5606 7204 8225 9360 10536
мясные,
млн. усл. банок.
Для анализа ряда динамики определите:
а) цепные и базисные абсолютные приросты, темпы роста, темпы прироста;
б) для каждого года значение 1% прироста;
в) в целом за весь период средний уровень ряда, среднегодовой абсолютный прирост, средний темп роста и средний темп прироста.
Изобразите на графике динамику производства мясных консервов с помощью столбиковой диаграммы.
Задача № 61.
Производство комбикорма в РФ характеризуется следующими данными:
Год 2000 2001 2002 2003 2004 2005 2006
Млн. т., 8,0 8,4 8,9 9,2 9,5 10,0 11,1
Для анализа ряда динамики определите:
а) базисные и цепные абсолютные приросты, темпы роста и темпы прироста;
б) для каждого года абсолютное значение 1% прироста;
в) среднегодовой уровень производства электроэнергии, среднегодовой абсолютный прирост, среднегодовые темп роста и темп прироста.
Нанесите на график динамику производства электроэнергии, используя фигурную диаграмму.
Задача № 62.
Среднегодовая численность населения области выглядит следующим образом:
| Годы | Среднегодовая численность населения, тыс. чел. |
По этим данным рассчитайте базисные и цепные показатели динамики. Результаты представьте в табличной форме. Отобразите на линейном графике динамику среднегодовой численности населения области.
Задача № 63.
Количество бирж по Российской Федерации (на конец года) составляет:
| Год | 2000 г. | 2001 г. | 2002 г. | 2003 г. | 2004 г. | 2005 г. |
| Количество бирж |
Определите:
1) среднегодовое число бирж;
2) цепные и базисные:
а) абсолютные приросты;
б) темпы роста;
в) темпы прироста;
3) средний абсолютный прирост;
4) среднегодовые темпы роста и прироста.
Сделайте выводы.
Задача № 64.
Используя взаимосвязь показателей динамики, определите уровни ряда динамики и недостающие в таблице базисные показатели динамики по следующим данным об урожайности сахарной свеклы:
| Год | Урожайность, ц/га | По сравнению с 2001 годом | ||
| Абсолютный прирост, ц/га | Темп роста, % | Темп прироста, % | ||
| 241,0 | --- | 100,0 | --- | |
| ? | 2,8 | ? | ? | |
| ? | ? | 110,3 | ? | |
| ? | ? | ? | 14,9 | |
| ? | ? | ? | 17,1 | |
| ? | ? | ? | ? | |
| ? | ? | 121,1 | ? |
Задача № 65.
Используя взаимосвязь показателей динамики, определите уровни ряда динамики и недостающие в таблице цепные показатели динамики по следующим данным о производстве продукции предприятиями объединения в сопоставимых ценах:
| Год | Производство продукции, млн. руб. | По сравнению с предыдущим годом | |||
| Абсолют- ный при рост, млн. руб. | Темп роста, % | Темп прироста, % | Абсолютное значение 1% прироста, млн. руб. | ||
| 92,5 | --- | --- | --- | --- | |
| ? | 4,8 | ? | ? | ? | |
| ? | ? | 104,0 | ? | ? | |
| ? | ? | ? | 5,8 | ? | |
| ? | ? | ? | ? | ? | |
| ? | 7,0 | ? | ? | 1,15 |
Задача № 66.
Остатки товаров в магазине характеризуются следующими данными:
Дата 1. 01 1.02 1. 03 1. 04 1. 05 1. 06 1. 07
тыс. руб. 310,5 320,0 315,4 320,8 317,0 321,3 325,9
Определите среднемесячные остатки товаров в магазине за I полугодие.
Задача № 67.
Динамика остатков вкладов на начало года по одному из ОСБ
Характеризуется следующими данными в тыс.руб.
Год 2003 2004 2005 2006 2007
Остатки вкладов 6287,3 26957,8 78209,3 175543,1 213378,7
Определите среднегодовые остатки вкладов за указанный период времени.
Задача № 68.
Имеются данные о вкладах граждан в банках:
| на 01.01. 2004 г. | на 01.02. 2004 г. | на 01.04. 2004 г. | на 01.08. 2004 г. | на 01.01. 2005 г. | |
| Вклады граждан в банках, млн. руб. | 480,5 | 580,6 | 754,8 | 850,3 | 980,4 |
Определите среднегодовую величину вкладов граждан в банках.
Задача № 69.
Численность работников организации с 1 марта до 10 марта была 280 человек, 10 марта были приняты 9 человек, 19 марта уволены 3 человека, 26 марта были приняты 8 и уволены 10. До конца месяца изменений не было. Определите среднюю списочную численность работников организации в марте.
Задача № 70.
Объем продукции предприятия в 2002 году был ниже объема ее в 2001 году на 2%; в 2003 году он составил 101% по отношению к объему 2002года, а в 2004 году был в 1,2 раза больше объема 2001 года. В 2005 году предприятие выпустило продукции на 15 млн. руб., что на 10% больше, чем в 2004году, в 2006 - на сумму 20 млн. руб. И в 2007 году - 27 млн. руб.
Определите абсолютные уровни производства продукции за все годы.
Задача № 71.
Произведите смыкание ряда динамики, используя следующие данные в сопоставимых ценах:
| Годы | |||||||
| Товарооборот области в прежних границах, млн. руб. | … | … | ... | ||||
| Товарооборот области в новых границах, млн. руб. | … | … | … |
Задача № 72.
Имеются данные о численности родившихся и умерших в РТ за ряд лет, чел.:
| Год | Родившихся | Умерших | Год | Родившихся | Умерших |
Рассчитайте базисные и цепные темпы роста численности родившихся и умерших. Сопоставьте динамику показателей с помощью коэффициентов опережения (отставания) рождаемости в сравнении со смертностью.
Задача № 73.
Производство продуктов земледелия характеризуется следующими данными, в тыс. тонн:
| Год | Сахарная свекла | Овощи | Картофель |
Для изучения общей тенденции производства продуктов земледелия произведите:
а) сглаживание уровней сахарной свеклы с помощью трехчленной скользящей средней;
б) аналитическое выравнивание уровней овощей по прямой.
в) аналитическое выравнивание уровней картофеля (выбор функции произвести самостоятельно)
Выровненные и фактические значения уровней картофеля наносите на график.
Задача № 74.
Имеются данные о результатах торгов акций компании 
:
| Дата | Цена закрытия, ден. ед. | Дата | Цена закрытия, ден. ед. |
| 05.01 | 28,48 | 19.01 | 28,35 |
| 09.01 | 28,38 | 22.01 | 28,43 |
| 10.01 | 28,39 | 23.01 | 28,39 |
| 11.01 | 28,35 | 24.01 | 28,40 |
| 12.01 | 28,33 | 25.01 | 28,38 |
| 15.01 | 28,32 | 26.01 | 28,35 |
| 16.01 | 28,33 | 29.01 | 28,36 |
| 17.01 | 28,43 | 30.01 | 28,39 |
| 18.01 | 28,35 | 31.01 | 28,42 |
1) Определите простые скользящие средние при интервале сглаживания, равном 3 дням, и интервале сглаживания, равном 5 дням;
2) Сравните графически исходный ряд динамики и ряды средних, полученных при интервалах сглаживания равным 3 дням и 5 дням. Укажите, какой ряд имеет более гладкий характер.
Задача № 75.
Средний курс акции компании за 12 дней составляет (долл.):
| День | 1-й | 2-й | 3-й | 4-й | 5-й | 6-й | 7-й | 8-й | 9-й | 10-й | 11-й | 12-й |
| Kt | 1,94 | 2,13 | 2,08 | 1,85 | 1,81 | 1,73 | 1,73 | 1,84 | 2,00 | 1,85 | 1,85 | 1,93 |
Рассчитайте коэффициенты линейного тренда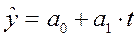 
, сделайте выводы. Отразите на графике фактические данные и результаты моделирования.
Задача № 76.
Грузооборот железных дорог в двух странах характеризуется следующими данными (млн. тарифных км.):
| Год | ||||||
| Страна А | ||||||
| Страна Б |
Для сравнительного анализа грузооборота железных дорог в странах А и Б приведите ряды динамики к общему основанию. Определите коэффициент опережения грузооборота железных дорог в стране А по сравнению со страной Б. Сделайте выводы.
Задача № 77.
Имеются данные по одному из предприятий:
| Год | Произведено продукции в сопоставимых ценах на 1 работающего, тыс. руб. | Фондоотдача, руб. | Удельный вес материалов в себестоимости, % |
| 44,2 | 20,6 | 95,5 | |
| 55,5 | 15,5 | 96,1 | |
| 43,8 | 10,3 | 97,2 | |
| 34,3 | 8,1 | 95,2 | |
| 42,3 | 8,5 | 95,2 | |
| 37,9 | 3,9 | 94,4 | |
| 32,6 | 5,3 | 94,8 | |
| 42,4 | 4,9 | 94,0 | |
| 42,9 | 3,7 | 92,9 | |
| 60,5 | 5,4 | 92,6 | |
| 61,5 | 5,0 | 80,5 | |
| 70,7 | 5,9 | 92,6 | |
| 80,5 | 6,8 | 93,9 | |
| 85,1 | 6,7 | 94,9 |
Для изучения общей тенденции производительности труда (выработки продукции на 1 работающего), использования основных фондов (фондоотдачи), материалоемкости продукции (удельного веса материалов в себестоимости ). Произведите: сглаживание уровней выработки, фондоотдачи и материалоемкости. Выбор функции осуществить самостоятельно. По результатам сглаживания сделайте выводы.
Задача № 78.
Имеются следующие данные о числе родившихся и числе зарегистрированных браков по месяцам за 2 года, тысяч:
| Месяц | Число родившихся, человек | Число зарегистрированных браков | ||
| Январь | 44,5 | 43,7 | 20,9 | 22,3 |
| Февраль | 39,5 | 38,1 | 21,9 | 22,9 |
| Март | 43,4 | 42,5 | 19,8 | 21,9 |
| Апрель | 41,8 | 41,4 | 22,6 | 19,6 |
| Май | 43,6 | 43,1 | 18,2 | 18,8 |
| Июнь | 43,2 | 42,3 | 22,4 | 23,2 |
| Июль | 44,3 | 43,9 | 26,9 | 24,3 |
| Август | 43,6 | 42,2 | 30,2 | 31,6 |
| Сентябрь | 41,2 | 40,2 | 25,3 | 25,3 |
| Октябрь | 41,2 | 39,9 | 24,8 | 25,1 |
| Ноябрь | 41,3 | 39,2 | 22,3 | 22,2 |
| Декабрь | 42,3 | 39,4 | 21,6 | 21,6 |
Для анализа внутригодовой динамики числа родившихся и числа зарегистрированных браков, определите коэффициенты сезонности методом простой средней арифметической.
Задача № 79
Имеются следующие условные данные о производстве мяса в одной из республик, тыс. т:
| Годы | |||
| Месяц | |||
| Январь | 109,2 | 80,7 | 80,4 |
| Февраль | 57,2 | 50,9 | 62,2 |
| Март | 56,2 | 85,3 | 48,6 |
| Апрель | 38,6 | 45,6 | 46,8 |
| Май | 39,0 | 55,8 | 54,4 |
| Июнь | 100,2 | 134,4 | 151,4 |
| Июль | 57,7 | 78,0 | 63,1 |
| Август | 118,6 | 124,2 | 120,3 |
| Сентябрь | 174,4 | 173,5 | 177,8 |
| Октябрь | 135,0 | 150,6 | 155,9 |
| Ноябрь | 84,1 | 111,0 | 130,7 |
| Декабрь | 69,1 | 56,2 | 80,2 |
Для анализа внутригодовой динамики производства мяса в республике рассчитайте коэффициенты сезонности методом простой средней арифметической. С помощью спиральной диаграммы изобразите сезонность производства мяса на графике. Сделайте выводы.
Решение типовых задач.
Задача 1.
По данным о вводе в действие жилых домов (таблица 1) рассчитать
1. Цепные, базисные и средние:
а) абсолютные приросты;
б) темпы роста;
в) темпы прироста;
2. Абсолютное значение 1% прироста.
Таблица 1
Ввод в действие жилых домов
| Текущий номер года,t | |||||
| Общая площадь, млн. кв. м. | 7,0 | 6,5 | 5,9 | 5,5 | 4,9 |
Решение:
Представим расчет цепных и базисных абсолютных приростов, темпов роста, темпов прироста в таблице 2.
Таблица 2
Статистические показатели динамики
| t | Уt, млн. кв. м. | Абсолютный прирост,млн. кв. м. | |
| Цепной | Базисный | ||
| 7,0 | - | - | |
| 6,5 | 6,5-7,0= -0,5 | 6,5-7,0= -0,5 | |
| 5,9 | 5,9-6,5= -0,6 | 5,9-7,0= -1,1 | |
| 5,5 | 5,5-5,9= -0,4 | 5,5-7,0= -1,5 | |
| 4,9 | 4,9-5,5= -0,6 | 4,9-7,0= -2,1 |
| t | Уt,млн. кв. м | Темп роста, % | |
Цепной 
| Базисный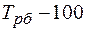 
| ||
| 7,0 | - | - | |
| 6,5 | (6,5:7,0)100=92,86 | (6,5:7,0)100=92,86 | |
| 5,9 | (5,9:6,5)100=90,77 | (5,9:7,0)100=84,29 | |
| 5,5 | (5,5:5,9)100=93,22 | (5,5:7,0)100=78,57 | |
| 4,9 | (4,9:5,5)100=89,09 | (4,9:7,0)100=70,00 |
| t | Уt, млн кв. м | Темп прироста, % | Абсолютное значение 1% прироста, млн.кв.м. | |
| Цепной | Базисный | 
| ||
| 7,0 | - | - | - | |
| 6,5 | 92,86-100= -7,14 | 92,86-100= -7,14 | 0,070 | |
| 5,9 | 90,77-100- -9,23 | 84,29-100= -15,71 | 0,065 | |
| 5,5 | 93,22-100= -6,78 | 78,57-100= -21,43 | 0,059 | |
| 4,9 | 89,09-100= -10,91 | 70,00-100= -30,00 | 0,055 |
Для получения обобщающих показателей динамики развития определим средние характеристики: средний абсолютный прирост, средний темп роста и средний темп прироста.
Средний абсолютный прирост равен:
то есть, в среднем ежегодно общая площадь вводимого жилья уменьшалась на 0,525 млн. кв. м.
Определим средний темп роста:
то есть, в среднем ежегодно строительство жилья составляло 91,47 % уровня базисного года.
Средний темп прироста 
то есть в среднем ежегодно строительство жилья снижалось на 8,53 %.
Задача 2.
Имеются следующие данные о поголовье крупного рогатого скота на 1 января:
Годы 1-ый 2-ой 3-ий 4-ый
Млн. голов 60,4 61,0 60,3 69,2
Определить среднегодовое поголовье крупного рогатого скота.
Решение:
Так как это моментный ряд с равным интервалом (1 год), то средний уровень ряда определяется по средней хронологической:
Задача 3.
Имеются данные об уровне запасов картофеля на начало года:
Годы 1-ый 5-ый 6-ой
Млн. т. 2103 2170 1584
Определить среднегодовой уровень запасов картофеля.
Решение:
Так как это моментный ряд с неравным интервалом, то среднегодовой уровень определяется по формуле средней скользящей взвешенной:
Задача 4.
Численность работников организации с 1 января до 9 января была 180 человек, 9 января были приняты 7 человек, 15 января уволены 2 человека, 25 января были приняты 5 и уволены 10. До конца месяца изменений не было. Определите среднюю списочную численность работников организаций в январе.
Решение:
Так как это интегральный ряд с неравным интервалом, то средний уровень ряда определяем по средней арифметической взвешенной:
Задача 5.
На основе данных о дневной выработке изделий А за 15 дней месяца произведите сглаживание ряда методом простой пятичленной скользящей средней:
Решение:
| Дни месяца | |||||||||||||||
| Выработка Изделий, шт. | |||||||||||||||
| Пятидневные скользящие средние | - | - | - | - |
Расчет пятидневной скользящей средней:
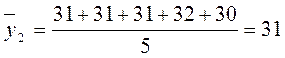
и т.д.
Задача 6.
Имеются данные, характеризующие валовый выпуск группы предприятий одной из отраслей в сопоставимых ценах (млрд. руб.):
| Годы | |||||||
| Валовый выпуск продукции: в старых границах области | - | - | - | ||||
| Валовый выпуск продукции В новых границах | - | - | - |
Привести ряд динамики к сопоставимому виду.
Решение:
1 способ: определяем для 2004г.коэффициент соотношения уровней двух рядов: 228:212 = 1,1 и умножаем его на уровни первого ряда:
2001 года 191∙1,1 = 210 млн. руб.
2002 года 197∙1,1 = 217 млн. руб.
2003 года 200∙1,1 = 220 млн. руб.
2 способ: для первого ряда уровень 2004 года 212 принимаем за 100%. Для второго ряда уровень 2004 года 228, принимаем за 100%. Остальные уровни пересчитываем:
2001 год 
и т. д.;
2007 год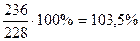 
и т. д.
Получим следующие ряды:
| Годы | |||||||
| Валовый выпуск продукции млн.руб | |||||||
| Валовый выпуск продукции в % к 2004 году | 90,1 | 92,9 | 94,3 | 100,0 | 103,5 | 107,5 | 114,9 |
Задача 7.
Имеются данные об урожайности овощей за 2002-2007 годы:
| Годы | t | yt | t2 | 
прямая
| yt2 | t 4 |
Пара
бола
| |
| -2 | -180 | |||||||
| -1 | -110 | |||||||
Для выявления тенденции урожайности овощей произведите аналитическое выравнивание по прямой и по параболе второго порядка.
Решение:
Уравнение прямой 
, где: t - время, а0 и а1 - параметры прямой, у - фактические значения урожайности. По методу наименьших квадратов решаем систему уравнений:
{ 
Эта система упрощается, если t подобрать так, чтобы их сумма равнялась нулю, т.е. начало отсчета времени перенести в середину рассматриваемого периода. Тогда St = 0, а уравнение примет вид:
{ 
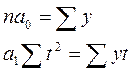
отсюда: 
Все расчеты делаем в табличной форме и находим параметры уравнения:
, а уравнение прямой 
Придавая различные значения t, (графа 3 таблицы) определяем выравненные значения урожайности. Например, за 2002 год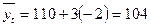 
и т.д.
Выбор кривой для аналитического выравнивания графическим методом показал, что ближе к фактическим значениям урожайности парабола второго порядка, уравнение которой. 
Решаем систему уравнений по способу наименьших квадратов:
{ 
При St = 0 и St3 = 0 система примет вид:
{ 
Расчеты делаем в табличной форме и подставляем в уравнение:
{ 
Отсюда: а0 = 125,1 а1 = 3 а2 = -7,86 
Придавая различные значения t (графа 3 таблицы), находим выравненные значения. Например, для 2002 года: 
Задача № 8.
При наличии данных о числе расторгнутых браков населением города по месяцам, за три года, выявите внутригодовую динамику разводов в городе на основании коэффициентов сезонности, рассчитанных методом простой средней арифметической.
| Месяц | Число расторгнутых браков | Число расторгнутых браков в среднем за три года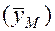 
| Коэффициент сезонности
| ||
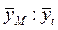
| Январь | 1,220 | ||||
| Февраль | 1,080 | ||||
| Март | 1,110 | ||||
| Апрель | 1,000 | ||||
| Май | 1,000 | ||||
| Июнь | 0,926 | ||||
| Июль | 0,926 | ||||
| Август | 0,890 | ||||
| Сентябрь | 0,868 | ||||
| Октябрь | 0,941 | ||||
| Ноябрь | 0,971 | ||||
| Декабрь | 1,022 | ||||
Средний
уровень
ряда 
| уt = 136 | 1,000 |
Решение:
Определяем среднюю одноименных месяцев.
Так средний январский уровень: 
Средний февральский: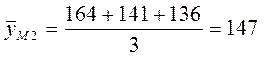 
и т.д.
Средний месячный уровень за 1994 год определяем так:
и т.д.
Выравненное значение:
расторгнутых браков или
расторгнутых браков.
Рассчитаем коэффициенты сезонности:
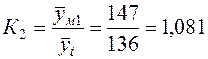и т.д.
Индексный метод
Задача № 80.
Имеются данные из отчетов сельхоз. предприятий о посевной площади и урожайности зерновых культур:
| Культура | Посевная площадь, га | Урожайность, ц/га | ||
| базисный период | отчетный период | базисный период | отчетный период | |
| Пшеница озимая | ||||
| Рожь | ||||
| Ячмень | ||||
| Кукуруза |
Определите:
а) индексы урожайности отдельных культур;
б) общий индекс урожайности;
в) общий индекс посевной площади;
г) индекс валового сбора;
д) прирост валового сбора за счет изменения урожайности зерновых культур;
е) покажите взаимосвязь индексов, вычисленных в пунктах б, в, г.
Задача № 81.
Имеются данные о ценах и количестве проданных товаров:
| Вид товара | Ед. измерения | Цена за единицу, руб. | Реализовано, тыс. ед. | ||
| предыдущий год | отчетный год | предыдущий год | отчетный год | ||
| Мясо | кг. | ||||
| Молоко | л. |
Определите:
1)общий индекс цен;
2)Общий индекс физического объема товарооборота;
3) общий индекс товарооборота.
Задача № 82.
Себестоимость и объем продукции завода характеризуются следующими данными:
| Изделие | Себестоимость единицы изделия, тыс. руб. | Выработано продукции, тыс. шт. | ||
| январь | Февраль | Январь | Февраль | |
Определите:
1) общий индекс затрат на все изделия;
2) общий индекс себестоимости продукции;
3) общий индекс физического объема продукции.
4) экономию (дополнительные затраты) от снижения (повышения) себестоимости продукции.
Задача № 83.
Имеются данные о численности и средней месячной заработной плате отдельных категорий промышленно-производственного персонала предприятия:
| Категории персонала | Среднемесячная заработная плата, руб. | Среднесписочная численность, человек | ||
| базисный период | отчетный период | базисный период | отчетный период | |
| Рабочие | ||||
| Служащие | ||||
| ИТР | ||||
| МОП и охрана |
Определите:
а) индексы заработной платы по каждой категории работников;
б) общий индекс заработной платы всех работников;
в) индекс численности работников;
г) индекс фонда оплаты труда;
д) экономию (перерасход) фонда оплаты труда за счет изменения заработной платы работников;
е) покажите взаимосвязь между индексами, вычисленными в пунктах б, в, г.
Задача № 84.
Имеются данные о произведенной продукции и затратах рабочего времени на производство продукции по кожгалантерейной фабрике за I и II полугодия отчетного года:
| Вид продукции | Выпущено продукции, тыс. шт. | Всего затрачено, чел/часов | |||
| 1 полугодие | 2 полугодие | 1 полугодие | 2 полугодие | ||
| Чемоданы | 15,3 | 16,8 | |||
| Портфели | 6,5 | 7,4 | |||
| Папки кожаные | 8,3 | 8,8 | |||
| Сумки школьные | 10,2 | 5,7 | |||
Определите:
а) общий индекс производительности труда;
б) экономию (дополнительные затраты) рабочего времени за счет изменения производительности труда;
в) индекс затрат рабочего времени;
г) индекс физического объема продукции;
д) индекс трудоемкости продукции
е) покажите взаимосвязь исчисленных индексов:
1) производительности труда, затрат рабочего времени и объема продукции;
2) трудоемкости продукции, физического объема продукции и затрат рабочего времен.
Задача № 85.
Имеются следующие данные:
| Вид изделия | Трудоемкость, чел/час | Объём выпускаемой продукции, тыс. шт. | ||
| базисный период | отчетный период | базисный период | отчетный период | |
| Кофемолка | 1,56 | 1,43 | 98,0 | 102,0 |
| Электрофен | 1,97 | 1,96 | 20,1 | 22,7 |
| Электробритва | 1,38 | 1,19 | 300,7 | 294,5 |
Вычислите:
а) индекс производительности труда;
б) индекс трудовых затрат.
Задача № 86.
Имеются данные о себестоимости и выпуске нескольких видов продукции предприятием:
| Изделия | Себестоимость единицы, руб. | Выпуск в отчетном периоде, тыс. шт. | ||||
| базисный период | Отчетный период | По плану | Фактически | |||
| по плану | фактически | |||||
| 10,0 | 9,5 | 9,0 | ||||
| 40,0 | 39,0 | 39,5 | ||||
| 23,0 | 22,0 | 20,0 | ||||
| 56,0 | 55,5 | 55,1 |
Определите:
а) плановое снижение себестоимости продукции (индекс планового задания);
б) индекс выполнения плана по снижению себестоимости продукции;
в) фактическое снижение себестоимости продукции (индекс динамики);
г) плановую экономию от снижения себестоимости;
д) фактическую экономию (дополнительные затраты) от изменения себестоимости продукции;
е) сверхплановую экономию (дополнительные затраты) от изменения себестоимости продукции.
Задача № 87.
Имеются следующие данные о продаже трикотажных изделий в одном из универмагов:
| Вид изделия | Базисная цена за 1изделие, руб. | Отчетная цена за 1изделие, руб. | Товарооборот отчетного периода, тыс. руб. |
| А | 18,7 | 15,0 | 1,42 |
| Б | 22,0 | 27,9 | 3,95 |
| В | 31,5 | 33,6 | 1,93 |
Определите:
а) среднее снижение (повышение) цен на данную группу товаров;
б) размер экономии (дополнительных затрат) населения от снижения (повышения) цен.
Задача № 88.
По одному из колхозных рынков города имеются данные:
| Товар | Товарооборот сентября, тыс. руб. | Изменение цен в сентябре по сравнению с июнем, % |
| Капуста свежая | -37,2 | |
| Лук репчатый | -37,7 | |
| Свекла столовая | 109,7 | -32,6 |
| Редис | 1,3 | + 5,5 |
Определите:
а) индекс цен;
б) индекс физического объема реализации с учетом того, что товарооборот сентября возрос на 52% по сравнению с июнем.
Задача № 89.
Имеются следующие данные по одному из цехов предприятия:
| Виды изделий | Выпуск продукции в базисном периоде, тыс. руб. | Изменение выпуска продукции в отчетном периоде по сравнению с базисным, % |
| А | +5 | |
| Б | -3 |
Вычислите общий индекс динамики физического объема продукции.
Задача № 90.
Имеются следующие данные о товарообороте овощей по одному из колхозных рынков:
| Товар | Товарооборот в ценах соответствующего периода, тыс. руб. | |
| Июнь | Сентябрь | |
| Морковь | ||
| Капуста свежая | ||
| Лук репчатый |
Вычислите средний процент изменения цен, если известно, что индекс физического объема реализации данных товаров составил 213%.
Задача № 91.
Имеются следующие условные данные:
| Изделия | Объем затрат на производство продукции, тыс. руб. | Изменение себестоимости изделия во 2 квартале по сравнению с первым, % | |
| базисный период | отчетный период | ||
| А | 95,2 | 110,7 | +5 |
| Б | 88,9 | 93,6 | -2 |
| В | 40,3 | 42,1 | без изменения |
Вычислите:
1) общий индекс затрат на производство изделий;
2) общий индекс себестоимости продукции;
3) общий индекс физического объема продукции;
4) абсолютное изменение затрат (тыс. руб.) за счет изменения себестоимости.
Задача № 92.
Имеются следующие данные о товарообороте по трем товарным группам за два периода:
| Ткани | Товарооборот, тыс. руб. | Среднее изменение цен в отчетном периоде по сравнению с базисным, % | |
| базисный период | отчетный период | ||
| Шерстяные | +4 | ||
| Шелковые | - 3 | ||
| Хлопчатобумажные | +8 |
Определите:
1)общий индекс цен;
2)общий индекс товарооборота;
3)общий индекс физического объема товарооборота;
4)сумму экономии (дополнительных расходов) населения от изменения цен.
Задача № 93.
Имеются следующие данные:
| Вид продукции | Затраты на производство продукции, тыс. руб. | Изменение физического объёма продукции в отчетном периоде по сравнению с базисным, % | |
| Базисный период | Отчетный период | ||
| А | -5,3 | ||
| Б | +1,0 | ||
| В | +2,5 |
Определите:
1) общий индекс физического объема продукции;
2) общий индекс затрат на производство продукции;
3) общий индекс себестоимости продукции.
Задача № 94.
Имеются следующие данные о производительности труда по двум цехам предприятия
| Всего отработано, чел./ час | Индексы производительности труда по каждому цеху, % | ||
| базисный период | отчетный период | ||
| Цех № 1 | 109,6 | ||
| Цех № 2 | 100,9 |
Определите:
1) общий индекс динамики производительности труда;
2) общий индекс затрат труда;
3) экономию затрат труда в результате роста его производительности
Задача № 95.
Производство мебели на одном из мебельных комбинатов характеризуется следующими данными:
| Вид продукции | Фактически произведено, штук | Сопоставимые цены за штуку, руб. | ||
| апрель | май | июнь | ||
| А | 40,2 | |||
| Б | 160,8 |
Определите:
1) индивидуальные индексы физического объема продукции (цепные и базисные);
2) общие индексы физического объема продукции (цепные и базисные);
3) покажите взаимосвязь базисных и цепных индексов.
Задача № 96.
Имеются следующие данные за I квартал:
| Изделия | Себестоимость 1 изделия, тыс. руб. | Выпуск продукции в натуральном выражении, шт. | ||||
| январь | февраль | март | январь | февраль | март | |
| А | 43,5 | 45,6 | 42,1 | |||
| Б | 30,2 | 29,8 | 32,6 |
Определите:
а) индивидуальные индексы себестоимости продукции (цепные и базисные);
б) общие индексы себестоимости продукции (цепные и базисные).
Задача № 97.
Имеются данные о выпуске продукции и себестоимости 1 тонны продукции на трех заводах области:
| Заводы | Произведено продукции, тыс. тонн | Себестоимость 1 т, руб. | ||
| базисный период | отчетный период | базисный период | отчетный период | |
| № 1 | 44,4 | 45,0 | ||
| № 2 | 13,3 | 15,0 | ||
| № 3 | 42,2 | 40,0 |
Определите:
а) изменение средней себестоимости продукции (индекс переменного состава);
б) индекс себестоимости продукции фиксированного состава;
в) индекс влияния структурных сдвигов в объеме продукции на себестоимость;
г) покажите взаимосвязь индексов;
д) сделайте выводы.
Задача № 98.
В экономическом районе добыча угля производится на шахтах и разрезах. За два года имеются данные:
| Способ добычи | Добыто угля, тыс. тонн | Средняя списочная численность, чел. | ||
| базисный год | отчетный год | базисный год | отчетный год | |
| Закрытый способ (на шахтах) | ||||
| Открытый способ (на разрезах) |
Определите:
а) индексы производительности труда (средней годовой добычи на 1 рабочего) отдельно на шахтах и на разрезах;
б) общую по району динамику производительности труда (индекс переменного состава);
в) индекс производительности труда фиксированного состава;
г) индекс влияния структурных сдвигов в численности рабочих на среднюю производительность труда;
д) проверьте результаты через взаимосвязь индексов;
Сделайте выводы.
Задача № 99.
Имеются следующие данные по двум цехам, выпускающим один вид продукции, но оснащенным различным оборудованием:
| Цех | Затраты времени на одну деталь, в чел./час | Фактически выработано деталей, тыс. шт. | ||
| базисный период | отчетный период | базисный период | отчетный период | |
| № 1 | 0,22 | 0,25 | 5,5 | 5,0 |
| № 2 | 0,05 | 0,04 | 24,0 | 25,2 |
Определите:
а) индексы производительности труда по каждому цеху;
б) общий индекс производительности труда по двум цехам (индекс переменного состава);
в) индекс производительности труда фиксированного состава;
г) индекс влияния структурных сдвигов;
Сделайте выводы.
Задача № 100.
По данным о продаже овощей на двух рынках города рассчитайте:
а) территориальный индекс цен;
б) территориальный индекс физического объема товарооборота, сравнивая рынок «А» с рынком «Б»:
| Наименование товара | Рынок «А» | Рынок «Б» | ||
| Количество проданных товаров, кг | Цена за 1 кг, руб. | Количество проданных товаров, кг. | Цена за 1 кг, руб. | |
| Картофель | ||||
| Морковь | ||||
| Свекла |
Задача № 101.
Определите территориальные индексы себестоимости и физического объема продукции по следующим данным двух заводов, сопоставив данные завода 1 с данными завода 2:
| Вид продукции | Завод 1 | Завод 2 | ||
| Количество продукции, шт. | Себестоимость 1шт., руб | Количество продукции, шт. | Себестоимость 1 шт., руб. | |
| А | ||||
| Б | ||||
| В |
Задача № 102.
Имеются данные о продаже молочных продуктов на рынках двух городов:
| Продукт | Цена за 1 кг, руб. | Объем продажи, кг | ||
| Город «А» | Город «Б» | Город «А» | Город «Б» | |
| Творог | ||||
| Сметана | ||||
| Масло животное |
Рассчитайте территориальные индексы цен и физического объема товарооборота на эти продукты в городе «А» по сравнению с городом «Б»
Задача № 103.
В марте по сравнению с январем продано товаров на 20 % меньше при среднем росте цен на 8 %. Определите изменение товарооборота.
Задача № 104.
При росте объема продукции на 18 % в отчетном периоде по сравнению с базисным общие затраты на производство продукции возросли на 13 %. Определите, как изменилась себестоимость единицы продукции.
Задача № 105.
На одном из заводов численность рабочих за первый год уменьшилась на 1,5 %, за второй на 3 %, за третий на 10 %. На сколько процентов уменьшилась численность рабочих за три года.
Задача № 106.
Как изменялась производительность труда, если физический объем продукции вырос на 8 %, а затраты труда на всю продукцию уменьшились на 5 %.
Задача № 107.
Стоимость продукции в сопоставимых ценах выросла на 7,5 %, производительность труда повысилась на 5,9 %. Определите, как изменились затраты труда на всю продукцию.
Задача № 108.
Как изменится производительность труда, если при том же объеме трудовых затрат количество продукции возрастет на 15 %.
Задача № 109.
Объем продукции предприятия в отчетном периоде уменьшился по сравнению с базисным на 5 %, а численность рабочих снизилась на 13 %. Определите, как изменилась производительность труда рабочих.
Задача № 110.
Заработная плата рабочих увеличилась на 20 %, а фонд оплаты труда уменьшился на 2 %. Как изменилась численность рабочих.
Решение типовых задач.
Задача № 1.
Имеются данные о продаже товаров в одном из регионов:
| Товар | Январь | Февраль | ||
| количество, q0 | цена за ед., руб., р0 | количество, q1 | цена за ед., руб., р1 | |
| А | 1,5 | 1,2 | ||
| Б | 5,0 | 5,5 |
Определите:
а) индивидуальные индексы цен и физического объема товарооборота;
б) общий индекс цен;
в) общий индекс физического объема товарооборота;
г) индекс товарооборота;
д) докажите взаимосвязь исчисленных индексов.
Расчет произведем в табличной форме, проставив необходимые обозначения:
| Индивидуальный индекс а) | Товарооборот | |||
| цен iр=р1/р0 | физического объема, iq=q1/q0 | отчетного периода, руб., p1q1 | базисного периода, руб., p0q0 | отчетного периода в ценах базисного периода, руб., p0q1 |
| 0,800 | 1,200 | |||
| 1,100 | 1,250 | |||
| х | x |
 | |||
 |
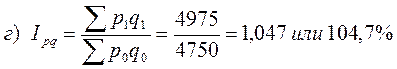
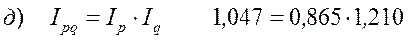
Задача № 2.
На основании приведенных данных определите индекс физического объема товарооборота:
| Товары | Товарооборот базисного периода, тыс. руб., p0q0 | Изменение количества продан- ных товаров, % (изм.) | Индивидуальный индекс физического объёма товарооборота,
100%±ИЗМ
 i q =
| Товарооборот отчетного периода в ценах базисного периода, тыс. руб., p0 q1= iq ∙ q0р0 |
| А | +15 | 1,15 | ||
| Б | +10 | 1,10 | ||
| Итого | x | x |
