Задача № 17.
Имеются следующие данные о потреблении некоторых видов продуктов населением РФ:
| Показатели | ||||
| Потребление в тыс. тонн: Мясо и мясопродукты | ||||
| Сахар-песок | ||||
| Хлеб и х/б изделия | ||||
| Среднегодовая численность населения, млн. чел. | 144,6 | 143,9 | 143,1 | 142,5 |
Определите потребление продукции на душу населения в РФ по годам. К какому виду относительных величин относятся исчисленные показатели? По результатам расчетов сделайте выводы.
Задача № 18.
По нижеприведенным показателям определите недостающие данные:
| Вид продукции | План, тыс. руб. | Фактически. тыс.руб. | % выполнения плана |
| Пальто женские зимние | ? | ||
| Пальто женские демисезонные | ? | ||
| Плащи женские | ? | ||
| Итого | ? | ? | ? |
Задача № 19.
План 2007 года по производству продукции на предприятии был выполнен на 107,3%. Фактический рост выпуска продукции в 2007 году составил 109,8%. Каково было плановое задание по производству продукции на предприятии?
Задача № 20.
Средняя урожайность зерновых в Российской Федерации составила 24 ц/га, а в Республике Татарстан - 26 ц/га. Сравните урожайность зерновых в Российской Федерации с урожайностью в Республике Татарстан.
Задача № 21.
Среднегодовая численность населения области составляла 2540,7 тыс. чел. Из них было занято в экономике 926,2 тыс. чел. Безработные составили 25,4 тыс. чел. Среди безработных лица с высшим образованием 3,0 тыс. чел, молодежь в возрасте 16-29 лет 7,8 тыс. чел., женщины- 18,4 тыс. чел. Определите удельный вес занятых и удельный вес безработных в численности всего населения, долю женщин, долю молодежи и долю людей с высшим образованием в числе безработных.
Задача № 22.
По данным управления социальной защиты населения администрации области на учете в органах социальной защиты населения состояло 663,3 тыс. пенсионеров, из них 528,1 тыс. чел. – пенсионеры по старости. Средний размер назначенной месячной пенсии с учетом компенсационных выплат составил 923 руб., в том числе по старости 937 руб.
Для характеристики пенсионного обеспечения в области рассчитайте удельный вес пенсионеров по старости в числе всех пенсионеров, во сколько раз пенсия по старости больше среднего размера назначенной пенсии. Какие виды относительных величин Вы рассчитали?
Задача № 23.
В трех партиях продукции, представленных на контроль качества, было обнаружено:
а) первая партия – 1000 изделий, из них – 920 качественных, 80 бракованных;
б) вторая партия – 800 изделий, из них – 730 качественных и 70 бракованных;
в) третья партия – 900 изделий, из них – 840 качественных и 60 бракованных.
Для характеристики качества продукции рассчитайте удельный вес качественной и бракованной продукции в каждой партии, сколько бракованных изделий приходится на 1000 качественных в каждой партии и в целом в трех партиях. Сравните исчисленные показатели и сделайте выводы.
Решение типовых задач.
Задача № 1.
Имеются данные о производстве мыла за отчетный и базисный периоды:
| Количество, тонн | % содержания жирных кислот | ||
| базисный период | отчетный период | ||
| Мыло | |||
| Мыло | |||
| Мыло |
Определите динамику производства мыла в натуральном измерении, в условно-натуральном измерении (40%-го мыла).
Решение:
Динамика производства мыла в натуральном выражении = 
=1.077 или 107.7%.
Для определения объема продукции в условно-натуральном измерении находим коэффициента пересчета мыла в 40%-е
мыло 40%- коэффициент = 1.0
мыло 60%- коэффициент = 60/40=1.2
мыло 80%- коэффициент = 80/40=2.0
Тогда динамика производства мыла в условно-натуральном измерении равна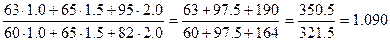 
или 109.0%.
Задача № 2.
По плану на 2004 год рост производства продукции по предприятию должен был составить 104,3%. Фактический рост выпуска продукции в 2004 году составил 104,8%. Как был выполнен план производства продукции на предприятии?
Решение:
Исходя из взаимосвязи относительных величин планового задания, выполнения плана и динамики, искомая относительная величина выполнения плана будет равна частному от деления относительной величины динамики на относительную величину планового задания
1.048:1.043=1.004 или 100.4%
Задача № 3.
Определите относительные величины структуры по данным о количестве проданных квартир в стране.
| Показатели | Количество квартир, тысяч | В %% к итогу (относит. величины структуры) |
| Всего продано квартир, в том числе: | 211.0 | 100.0 |
| государственного | 184.3 |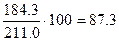 
|
| общественного | 26.7 |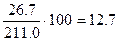 
|
Задача № 4.
На начало 2002-2003 учебного года численность студентов высших учебных заведений Республики Татарстан составляла 170,8 тыс. чел., а численность всего населения 3777,7 тыс. чел. Определите относительную величину интенсивности (количество студентов на 1000 человек населения,‰).
Решение:
170,8 тыс. чел. студентов: 3777,7 тыс. чел. населения х 1000=45,2‰
(45 человек на 1000 человек населения). 
Задача № 5.
Имеются следующие условные данные о пассажирообороте отдельных видов транспорта общего пользования за год, пассажиро - километров.
| Вид транспорта | Пассажирооборот |
| Автобусный | 6650.9 |
| Троллейбусный | 416.1 |
| Трамвайный | 1061.2 |
| Железнодорожный | 3200.0 |
| Воздушный | 739.1 |
| Внутренний водный | 69.1 |
Определите, сколько пассажиро–километров каждого вида транспорта приходится на 1000 пассажиро –километров железнодорожного транспорта. К какому виду относительных величин относится исчисленные показатели?
Решение:
| Вид транспорта | Пассажирооборот (пассажиро - километры на 1000 пассажиро - километров железнодорожного транспорта), ‰. |
| Автобусный | 6650,9:3200∙1000=2078,4 |
| Троллейбусный | 416,1:3200∙1000=130,0 |
| Трамвайный | 1061,2:3200∙1000=331,6 |
| Воздушный | 739,1:3200∙1000=231,0 |
| Внутренний водный | 69,1:3200∙1000=21,6 |
Рассчитанные показатели в промилле (‰) являются относительными величинами координации, т. к. характеризуют соотношение частей целого между собой.
Задача № 6.
Средняя урожайность картофеля в Российской Федерации 106 ц/га, а в Республике Татарстан-122 ц/га. Сравните урожайность картофеля в Российской Федерации с урожайностью в Республике Татарстан.
Решение:
Относительная величина сравнения 
Средние величины
Задача № 24.
Квалификация одной из бригад предприятия характеризуется следующими данными:
Порядковый номер рабочих 1 2 3 4 5 6 7
Разряд тарифной сетки 5 4 2 6 3 5 4
Определите средний тарифный разряд рабочих бригады.
Задача № 25.
Рассчитайте среднюю купюрность денег, выпущенных в обращение:
Достоинство
купюр, руб. 1 2 5 10 50 100 500 1000 5000
Выпущено в
обращение, 540 500 710 620 600 500 300 100 5
млн. штук
Задача № 26.
В районе в результате проверки двух партий бананов перед отправкой их потребителям установлено, что в первой партии весом 6248 кг. высшего сорта было 46,2 %, во второй партии из 7647 кг. – 68,3% высшего сорта.
Определите процент бананов высшего сорта в среднем по двум партиям вместе по району.
Задача № 27.
Имеются следующие данные о распределении фермерских хозяйств по размеру земельных угодий:
| Земельные угодия, га. | Число хозяйств, ед. |
| До 3 | |
| 4-5 | |
| 6-10 | |
| 11-20 | |
| 21-50 | |
| 51-70 | |
| 71-100 | |
| Свыше100 |
Определите средний размер земельных угодий.
Задача № 28.
Определите среднюю дневную выработку одного рабочего на основании следующих сгруппированных данных:
| Дневная выработка (м) | Количество рабочих, чел |
| 50-60 | |
| 60-80 | |
| 80 и более | |
| Итого: |
Задача № 29.
На основании следующих данных определите средний процент бракованной продукции в трех партиях продукции в целом:
| Номер партии продукции | Процент бракованной продукции | Удельный вес партии во всей продукции, % |
| Первая | 8,0 | 37,0 |
| Вторая | 9,6 | 29,6 |
| Третья | 6,7 | 33,4 |
Задача № 30.
Имеются следующие данные по населению города:
| Группы населения по возрасту, лет | Численность населения, тыс. чел. | Возрастная структура, % | ||
| Всего населения | мужчин | женщин | ||
| до 15 | 66,07 | 17,9 | 18,8 | 17,0 |
| 15 - 45 | 162,77 | 44,1 | 45,9 | 42,3 |
| 45 - 65 | 84,98 | 23,0 | 23,2 | 22,8 |
| свыше 65 | 55,52 | 15,0 | 12,1 | 17,9 |
| Итого | 369,34 | 100,0 | 100,0 | 100,0 |
Определите средний возраст населения города, а также средний возраст мужчин и женщин.
Задача № 31.
По нижеследующим данным за два периода по группе сельскохозяйственных предприятий определите среднюю урожайность свеклы в каждом периоде
| сельхоз. предприятия | базисный период | отчетный период | ||
| урожайность, ц/га | посевная площадь, га | урожайность, ц/га | валовый сбор, тонн | |
Задача № 32.
Имеются следующие данные по четырем заводам, выпускающим одноименную продукцию за отчетный период:
| № завода п/п | Выработано одноименной продукции, тыс. тонн | Себестоимость 1 тонны, руб. | Месячный фонд заработной платы, тыс. руб. | Средняя месячная заработная плата, руб. |
Определите в целом по всем заводам: а) среднюю себестоимость 1 тонны продукции; б) среднюю заработную плату работающих.
Задача № 33.
Выпуск продукции двумя цехами завода за базисный и отчетный периоды характеризуется следующими данными:
| Номер цеха | Базисный период | Отчетный период | ||
| удельный вес продукции 1 сорта, % | стоимость продукции 1 сорта, тыс. руб. | удельный вес продукции 1 сорта, % | стоимость всей произведенной продукции, тыс. руб. | |
Определите средний удельный вес продукции 1 сорта по двум цехам вместе в базисном и отчетном периодах.
Задача № 34.
По двум промышленным предприятиям одного объединения имеются следующие данные: первое предприятие выпустило продукции на сумму 8000 тыс. руб. и выполнило план на 95%. Второе предприятие произвело продукции на 9000 тыс. руб. и выполнило план на 102%. Определите средний процент выполнения плана по двум предприятиям объединения вместе.
Задача № 35.
По нижеприведенной группировке магазинов по размеру товарооборота определите моду и медиану.
Товарооборот,
тыс. руб. до 50 50-100 100-150 150-200 200-250 Всего
Число магазинов 10 13 11 9 7 50
Задача № 36.
Известно следующее распределение вкладчиков отделения Сбербанка по размеру вкладов:
| Вклады, тыс. руб. | Число вкладчиков, тыс. чел. |
| До 50 | 168,0 |
| 50-100 | 29,0 |
| 100-500 | 13,0 |
| 500-1000 | 3,0 |
| 1000-5000 | 1,0 |
| 5000 и более | 0,1 |
| Итого | 214,1 |
Определите средний, модальный и медианный размер вклада.
Решение типовых задач
Задача № 1.
В двух бригадах выработка одноименной продукции за смену характеризуется следующими данными:
| Бригада 1 | Бригада 2 | ||
| Выработка продукции на 1 раб., шт. | Число рабочих, чел | Выработка продукции на 1 раб., шт. | Число рабочих, чел |
Определите в какой бригаде и на сколько выше средняя выработка продукции на одного рабочего. Какой вид средней использован для расчета выработки в каждом случае?
Решение:
Для определения средней выработки по первой бригаде используется формула средней арифметической простой 
, где x-выработка в каждой группе рабочих, а n-число групп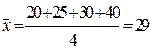 
(шт.), т.к. каждый вариант выработки встречается равное (по 25) число раз.
Для определения средней выработки по второй бригаде используется формула средней арифметической взвешенной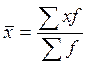 
, где x-выработка в каждой группе рабочих, а f-число рабочих в каждой группе.
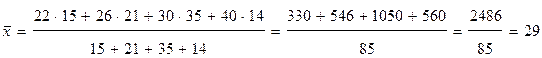(шт.), т.к. каждый вариант выработками встречается разное число раз.
Следовательно, средняя выработка в бригадах одинаковая.
Задача № 2.
Требуется вычислить среднюю цену продукта «А» в отчетном и базисном периодах на основании данных по двум рынкам города:
| Рынки | Базисный период | Отчетный период | ||
| цена за 1 кг, руб. | Продано, кг | цена за 1 кг, руб. | выручка, тыс. руб. | |
| (x) | (f) | (x) | (M) | |
| А | 35.56 | |||
| Б | 14.88 | |||
| Итого | X | X | 50.44 |
Решение:
В базисном периоде среднюю цену продукта определяем по средней арифметической взвешенной, т.к. средняя цена: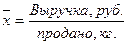 
,где знаменатель дроби известен (вес проданного продукта), а числитель (выручку) определяем путем умножения цены 1 кг продукта на количество в кг.
Среднюю цену в отчетном периоде следует вычислять по средней гармонической взвешенной, т.к. числитель дроби известен (выручка), а знаменатель дроби (продано, кг) можно определить путем деления суммы выручки по каждому рынку на цену 1 кг.
.
Задача № 3.
Имеются данные о выполнении плана на двух предприятиях за два периода:
| № предприятия | Базисный период | Отчетный период | ||
| выполнение плана, % | фактический выпуск продукции тыс. руб. | выполнение плана, % | плановый объем продукции тыс. руб. | |
| Итого | x | x |
Необходимо определить средний процент выполнения плана на двух предприятиях в базисном и отчетном периодах.
Решение:
Т.к. процент выполнения плана - это отношение: 
В базисном периоде средний процент выполнения плана определяем по средней гармонической взвешенной, т.к. числитель дроби известен (фактический выпуск), а знаменатель дроби (плановый объем) находим как частное от деления фактического выпуска на коэффициент выполнения плана.
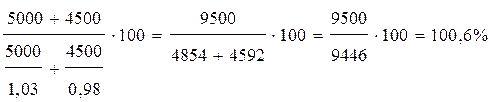
В отчетном периоде средний процент выполнения плана определяем по средней арифметической взвешенной, т.к. знаменатель дроби известен (плановый объем), а числитель дроби можно определить как произведение коэффициента выполнения плана по каждому заводу на плановый объем продукции.
Задача № 4.
Рабочие завода распределены по возрасту следующим образом:
| Группы рабочих по возрасту, лет (x) | Число рабочих (f) | Сумма накопленных частот (s) |
| до 20 | ||
| 20-30 | ||
| 30-50 | ||
| 50 и более |
Определите моду и медиану:
Решение:
Модальным будет интервал 20 – 30, так как встречается чаще (255 рабочих). Отсюда
Медианным будет интервал 20 – 30, так как половина рабочих 
находится в этой группе 
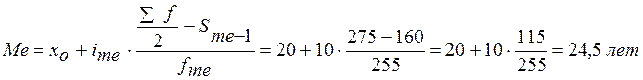
Задача № 5.
На основании нижеследующих данных определите:
а) средний размер основных фондов на один завод (упрощенным способом):
| Группы заводов по размеру основных фондов, млн. руб. | Число заводов (f) | Середина интервала (x) | x-А А=9 | 
i=2
| 
|
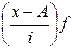
| 4-6 | -4 | -2 | -4 | ||
| 6-8 | -2 | -1 | -3 | ||
| 8-10 | |||||
| 10-12 | |||||
| 12-14 | |||||
| Итого | Х | Х | Х |
 |
Решение:
Т.к. интервал группировки равный, для расчета используем упрощеный метод моментов: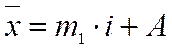 
,где m1 момент первой степени 
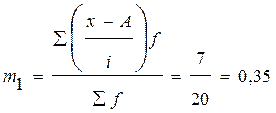, тогда средний размер основных фондов
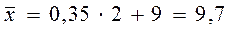(млн. руб.)
Показатели вариации
Задача № 37.
Население области за отчетный год по размеру среднедушевого дохода распределилось следующим образом:
| Среднедушевой доход в месяц, тыс. руб. | Население, тыс. чел. |
| до 1,0 | 130,3 |
| 1,0 - 2,5 | 1160,0 |
| 2,5 - 4,5 | 985,4 |
| 4,5 - 7,0 | 354,2 |
| 7,0 - 10,0 | 91,8 |
| 10,0 и более | 26,8 |
| Всего | 2748,5 |
Рассчитайте среднедушевой доход населения области за месяц и его вариацию. Оцените уровень колеблемости среднедушевого дохода населения с помощью размаха вариации, среднего линейного отклонения и коэффициента вариации по среднему линейному отклонению. Сделайте выводы.
Задача № 38.
Имеются данные о распределении рабочих предприятия по размеру месячной заработной платы:
| № группы | Месячная заработная плата рабочих, руб. | Число рабочих, % |
| До 6000 | ||
| 6000-7000 | ||
| 7000-8000 | ||
| 8000-9000 | ||
| 9000-10000 | ||
| 10000-11000 | ||
| 11000 и более | ||
| Итого |
Определите: а) средний размер месячной заработной платы всех рабочих предприятия; б) дисперсию; в) среднее квадратическое отклонение; г) коэффициент вариации.
Задача № 39.
По результатам обследования 40 сельхоз. предприятий области получены следующие данные:
| Группы сельхоз. предприятий по среднему годовому надою молока от одной коровы, кг. | Число сельхоз. предприятий |
| до 2000 | |
| 2000-2200 | |
| 2200-2400 | |
| 2400-2600 | |
| 2600-2800 | |
| 2800-3000 | |
| 3000 и более | |
| Итого |
Определите: а) средний годовой надой молока от одной коровы по всем сельхоз. предприятиям области; б) дисперсию; в) среднее квадратическое отклонение; г) коэффициент вариации.
Задача № 40.
Имеются данные о распределении 100 магазинов по величине товарооборота:
| Группы магазинов по величине товарооборота, тыс. руб. | Число магазинов |
| до 100 | |
| 100-200 | |
| 200-350 | |
| 350-600 | |
| Итого |
Определите: а) среднюю величину товарооборота на один магазин по всем предприятиям; б) дисперсию; в) среднее квадратическое отклонение; г) коэффициент вариации. Сделайте выводы.
Задача № 41.
Имеются данные о распределении предприятий по численности работников:
| Группы предприятий по численности работников, чел. | Количество предприятий |
| до 500 | |
| 500-700 | |
| 700-1000 | |
| 1000 и более |
Определите: а) среднюю численность работников на одном предприятии; б) дисперсию; в) среднее квадратическое отклонение; г) коэффициент вариации; д) модальную и медианную численность работников.
Задача № 42.
Распределение рабочих двух заводов одного объединения по тарифным разрядам характеризуется следующими данными:
| Тарифный разряд | Численность рабочих на заводах | ||
| № 1 | №2 | Итого | |
Определите: а) средний тарифный разряд по каждому заводу и по объединению; б) дисперсию по каждому заводу и общую по объединению;
в) среднюю из групповых дисперсий; г) межгрупповую дисперсию. Результаты проверьте правилом сложения дисперсий.
Задача № 43.
Ниже приводится группировка рабочих - сдельщиков предприятия по проценту выполнения норм выработки.
| Процент выполнения норм выработки | Число рабочих по цехам предприятия | ||
| №1 | №2 | Итого | |
| до 80 | |||
| 80-100 | |||
| 100-120 | |||
| 120-140 | |||
| 140 и более | |||
| Итого |
Определите: а) средний процент выполнения норм выработки в каждой группе рабочих и по всей совокупности рабочих; б) дисперсии групповые и общую; в) среднюю из групповых дисперсий; г) межгрупповую дисперсию. Результаты проверьте правилом сложения дисперсий.
Задача № 44.
Имеются выборочные данные об урожайности пшеницы:
| Урожайность, ц/га | Площадь, занятая под пшеницей, га | ||
| Яровой | Озимой | Итого | |
| до 20 | |||
| 20-24 | |||
| 24-28 | |||
| 28 и более | |||
| Итого |
Определите: а) среднюю урожайность яровой пшеницы, озимой пшеницы и всей пшеницы в целом; б) дисперсию признака по каждому виду пшеницы и всей пшенице; в) среднюю из групповых дисперсий; г) межгрупповую дисперсию; д) результаты проверьте правилом сложения дисперсий; е) модальную величину урожайности яровой и озимой пшеницы; ж) медианную величину урожайности яровой и озимой пшеницы.
Решение типовых задач
Задача № 1.
По данным об урожайности винограда на различных участках определите: а) размах вариации; б) среднюю урожайность винограда; в) среднее линейное отклонение; г) дисперсию; д) среднее квадратическое отклонение; е) коэффициент вариации по среднему линейному отклонению.
| № участка | Урожайность винограда с одного куста, кг.(x) | Число кустов (f) |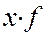 
| 
| 
| 
|
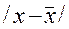
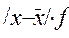
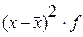
| 3,9 | 19,5 | 76,05 | ||||
| 2,9 | 20,3 | 58,87 | ||||
| 1,9 | 15,2 | 28,88 | ||||
| 0,9 | 9,9 | 8,91 | ||||
| 0,1 | 1,5 | 0,15 | ||||
| 1,1 | 17,6 | 19,36 | ||||
| 2,1 | 21,0 | 44,10 | ||||
| 3,1 | 24,8 | 76,88 | ||||
| Итого | Х | Х | 129,8 | 313,20 |
Решение:
а) размах вариации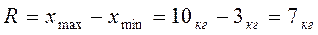 
б) средняя урожайность 
(кг).
в) среднее линейное отклонение
(кг).
г) дисперсия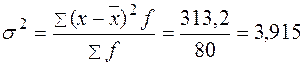 
.
д) среднее квадратическое отклонение 
(кг)
е) по среднему линейному отклонению: коэффициент вариации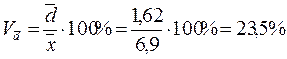 
.
Задача № 2.
На основании нижеследующих данных определите: а) средний размер основных промышленно-производственных фондов на один завод (упрощенным способом); б) дисперсию (упрощенным способом); в) среднее квадратическое отклонение; г) коэффициент вариации.
| Группы заводов по стоимости основных фондов, млн. руб. | Число заводов (f) | Середина интервала (x) | x-А А=9 | 
| 
| 
|
| 4-6 | -4 | -2 | -4 | |||
| 6-8 | -2 | -1 | -3 | |||
| 8-10 | - | - | - | - | ||
| 10-12 | ||||||
| 12-14 | ||||||
| Итого | Х | Х | Х |
Решение:
Так как интервал группировки равный, для расчета можно использовать упрощенный метод моментов (и для средней, и для дисперсии).
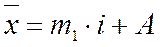
а) средний размер основных фондов
где m1 момент первой степени
, тогда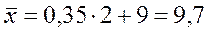 
(млн. руб.).
б) дисперсия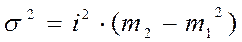 
, где m2 момент второй степени.
, тогда
в) среднее квадратическое отклонение 
(млн. руб.).
г) коэффициент вариации 
Задача № 3.
По нижеследующим данным определите: а) среднюю урожайность озимой пшеницы; б) дисперсию (упрощенным способом); в) среднее квадратическое отклонение; г) коэффициент вариации.
| Урожайность, ц/га | Посевная площадь, га. (f) | Середина интервала (x) | Сокращенные веса в 50 раз (f) | xf | x2f |
| 20-22 | 21,0 | 63,0 | 1323,00 | ||
| 22-25 | 23,5 | 23,5 | 552,25 | ||
| 25-30 | 27,5 | 55,0 | 1512,50 | ||
| 30-40 | 35,0 | 140,0 | 4900,00 | ||
| Итого |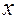 
| 281,5 | 8287,75 |
а) средняя урожайность 
ц/га;
б) так как интервал группировки, неравный дисперсия упрощенным способом
;
в) среднее квадратическое отклонение
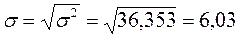ц/га;
г) коэффициент вариации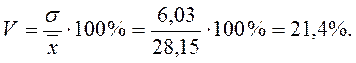 
Задача № 4.
По нижеследующим данным о группировке магазинов по размеру товарооборота определите: а) среднюю величину товарооборота на один магазин по каждому району и в целом по всей совокупности магазинов; б) дисперсию признака по каждому району и в целом по всей совокупности магазинов; в) среднюю из групповых дисперсий; г) межгрупповую дисперсию; д) результаты проверьте правилом сложения дисперсий; е)для характеристики влияния на вариацию территориального признака рассчитайте эмпирический коэффициент детерминации и корреляционное отношение.
| Группы магазинов по величине товарооборота, тыс. руб. | Число магазинов | ||
| Район А | Район Б | Итого | |
| 400-600 | |||
| 600-800 | |||
| 800-1000 | |||
| 1000-1200 | |||
| 1200-1400 | |||
| Итого |
Решение: Промежуточные расчеты делаем в табличной форме:
| Группы магазинов по величине товарооборота, тыс. руб. | Число магазинов | Cередина интервала (x) | x-A A=900 |  i=200
| 
| 
| 
| 
| 
| 
| ||
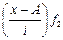
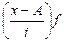
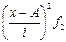
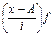
| Район А (f1) | Район Б (f2) | Итого (f) | ||||||||||
| А | ||||||||||||
| 400-600 | - 400 | -2 | -12 | -6 | -18 | |||||||
| 600-800 | - 200 | -1 | -17 | -20 | -37 | |||||||
| 800-1000 | - | - | - | - | - | - | - | - | ||||
| 1000-1200 | ||||||||||||
| 1200-1400 | ||||||||||||
| Итого | x | x | x |
Тогда средний товарооборот определяется по методу моментов:
где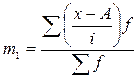 
тыс. руб.- средний товарооборот одного магазина в районе А;
тыс. руб.- средний товарооборот одного магазина в районе Б;
тыс. руб.- средний товарооборот одного магазина по всей совокупности магазинов.
б) 
, где 
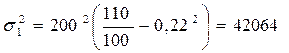- дисперсия по району А;
- дисперсия по району Б.
- дисперсия общая.
в) средняя из внутригрупповых дисперсий
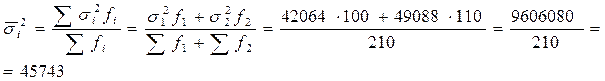г) межгрупповая дисперсия
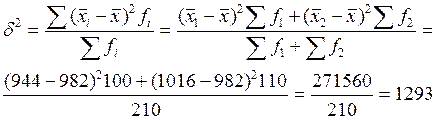
д) правило сложения дисперсий
т.е. 
,полученная по методу моментов 46992 
4700 равна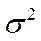 
,полученной как сумма средней из групповых дисперсий и межгрупповой дисперсии 47036 47000.
е)эмпирический коэффициент детерминации
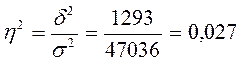
Следовательно, на группировочный территориальный признак (деление на районы) приходится лишь 2,7% вариации и слабо связан с товарооборотом магазинов, т.к. корреляционное отношение равно
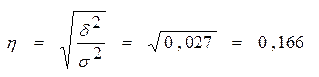
Выборочное наблюдение
Задача № 45.
Для определения срока службы оборудования было проведено 10%-е выборочное обследование по методу случайного бесповторного отбора, в результате которого получены следующие данные:
| Срок службы, лет | Количество оборудования |
| До 4 | |
| 4-6 | |
| 6-8 | |
| 8-10 | |
| 10 и более | |
| Итого |
1) С вероятностью 0,997 определите предельную ошибку выборки и пределы, в которых ожидается средний срок службы оборудования.
2) С вероятностью 0,954 определите предельную ошибку репрезентативности для доли и пределы удельного веса оборудования со сроком службы более 10 лет.
Задача № 46.
Принимая распределение оборудования по сроку службы, приведенного в задаче № 45, за результаты ранее проведенного выборочного наблюдения, рассчитайте, какое количество оборудования подвергнуть наблюдению при условии, что предельная ошибка выборки при определении среднего срока службы была бы не более одного года при вероятности 0,997, а предельная ошибка доли оборудования со сроком службы 8-10 лет при вероятности 0,954 была бы не более 5%.
Задача № 47.
Для оценки средней урожайности пшеницы посевную площадь совхоза в 5000 га разделили на 50 равных участков. Из них по методу случайной бесповторной выборки отобрали пять участков, где произвели сплошной учет фактического урожая. В результате были получены следующие данные:
| Показатели | Номер участка | ||||
| Средняя урожайность, ц/га | |||||
| Погибшие посевы, % | 3,0 | 2,5 | 2,0 | 1,5 | 1,0 |
Определите:
1) С вероятностью 0,997 предельную ошибку выборочной средней и границы, в которых будет находиться средняя урожайность по совхозу;
2) С вероятностью 0,954 предельную ошибку выборочной доли и границы, в которых будет находиться процент погибших посевов пшеницы.
Задача № 48.
С целью определения среднего эксплутационного пробега 10000 шин легковых автомобилей, распределенных на партии по 100 штук, проводится серийная 4%-я бесповторная выборка. Результаты испытания отобранных шин характеризуются следующими данными:
| Показатели | Партии | |||
| Средний эксплутационный пробег шин, тыс. км. | ||||
| Доля шин с пробегом не менее 42 тыс.км. | 0,80 | 0,85 | 0,90 | 0,95 |
Определите:
1) среднюю ошибку репрезентативности эксплутационного пробега шин;
2) среднюю ошибку репрезентативности удельного веса шин с пробегом не менее 42 тыс. км;
3) С вероятностью 0,954 пределы, в которых будет находиться средний эксплутационный пробег всех исследуемых шин;
4) С вероятностью 0,954 пределы, в которых будет находиться доля шин, пробег которых не менее 42 тыс. км. в генеральной совокупности.
Задача № 49.
Используя условие и решение задачи № 48, определите вероятность того, что:
1) предельная ошибка выборки при установлении среднего эксплутационного пробега шин не превышает 40 тыс. км.;
2)доля шин с пробегом не менее 42 тыс. км. будет находиться в пределах 83%-92%.
Решение типовых задач.
Задача №1.
Для проверки веса чая в пачках произведена 25%-я механическая выборка, по результатам которой получены следующие данные:
| Вес пачки чая, грамм. | Количество пачек |
| 47-49 | |
| 49-51 | |
| 51-53 | |
| 53-55 | |
| Итого |
Определить:
1) С вероятностью 0,954 предельную ошибку выборки и границы, в которых можно ожидать средний вес пачки чая во всей партии;
2)С вероятностью 0,954 предельную ошибку выборки для доли пачек чая весом 51-55 грамм.
Решение:
Для нахождения среднего веса пачки чая в выборочной совокупности можно использовать метод моментов, т.к. интервал группировки равный. Расчетная таблица:
| Вес пачки чая, грамм. | Количество пачек (f) | Середина интервала (x) | x-A A=50 | 
I=2
| 
| 
|
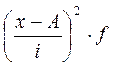
| 47-49 | -2 | -1 | -20 | |||
| 49-51 | - | - | - | - | ||
| 51-53 | ||||||
| 53-55 | ||||||
| Итого | Х | Х | Х |
1) Средний вес пачки чая в выборочной совокупности
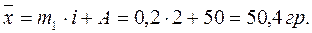т.к.
При бесповторном отборе предельная ошибка выборки для среднего веса пачки чая определяется по формуле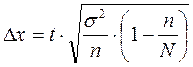 
, где t-коэффициент доверия, равный при вероятности 0,954 двум, n-численность выборочной совокупности, равная 100, N-численность генеральной совокупности, равная при 25% отборе 
. Дисперсия среднего веса пачки чая в выборочной совокупности по методу моментов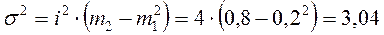 
. Т.к.
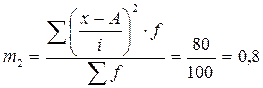
Следовательно границы генеральной средней будут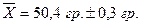 
2) Предельная ошибка доли пачек чая с весом 51-55 гр. При бесповторном отборе определяется по формуле 
, где w-доля пачек чая с весом 51-55 гр. В выборочной совокупности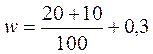 
или 30% 
или 8%
Тогда доля пачек с весом 51-55 грамм в генеральной совокупности будет находиться в пределах 
или 22%≤Р≤38%.
Задача №2
Используя данные и решение задачи №1 определить, какое число пачек чая следует подвергнуть наблюдению при условии, что предельная ошибка выборки для бесповторного отбора при определении среднего веса пачки чая была бы не более 0,1 грамма при вероятности 0,997, а предельная ошибка доли пачек чая с весом 51-55 грамм была бы не более 3%.
Решение:
Для определения численности выборочной совокупности при механическом бесповторном отборе используются формулы:
Для средней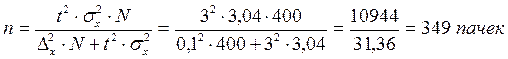 
Для доли 
