Теорема 1: Скорость любой точки на механизме равна по величине и направлению скорости соответствующей точке на рычаге Жуковского
Докажем: 
но 
; PD = ppd последнее принято при построении, следовательно скорости равны по величине, но они равны и по направлению, т.к. обе перпендикулярны вектору ppd на рычаге.
, 
, 
, 
, 
Следствие: рычагом Жуковского можно пользоваться, как планом скоростей.
Теорема 2: Если силу механизма перенести параллельно самой себе на рычаг Жуковского, то мощность этой силы на механизме будет равна мощности той же силы на рычаге Жуковского.
;
.
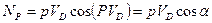Следствие: 
, т.е. мощность любой силы равна моменту этой силы, относительно полюса и угловой скорости рычага (произведению).
Теорема 3: Если все силы уравновешенны на механизме перенести параллельно, в соответствующие точки рычага, то сумма моментов всех сил относительно полюса рычага равны нулю.
Если силы на механизме уравновешенны, то сумма их мощностей равна 0. Но мощности на рычаге и на механизме равны, следовательно сумма мощностей сил на рычаге тоже будет равна 0.
, 
Следствие: для нахождения движущего момента на начальное звено нужно: перенести с механизма на рычаг все силы параллельно себе в соответствующие точки, включая движущий момент; затем нужно составить сумму моментов относительно полюса рычага, и решить её относительно движущего момента (силы инерции так же включаются).
Два способа переноса момента с механизма на рычаг Жуковского.
I способ:
Момент силы приводят к двум точкам звена, направляя силы в этих точках согласно знаку момента. Сила P2 в этих точках равна: 
: затем силы переносятся на рычаг в соответствующие точки параллельно самим себе.
II способ:
Момент силы переносят на рычаг Жуковского из условия равенства их мощностей М – момент силы на механизме, М’ – на рычаге.
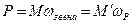; Р – мощность момента сил на механизме.
Направление М’ определяют из условия знаков 
и 
. Если угловые скорости направлены в одну сторону ( и один знак), то момент силы не меняет своего направления. При разных знаках момент при переносе должен изменить своё направление.
, 
Тема: Динамическое исследование механизма.
– уравнение кинетической энергии.
Определение: Приращением кинетической энергии за промежуток времени равно сумме работ всех внешних и внутренних сил механизма.
1. 
; 
работа движущих сил.
2. 
; 
работа сил полезного сопротивления.
3. 
; 
работа сил трения.
4. 
; 
работа сил веса.
5. 
; 
.
6. 
; 
работа сил сопротивления.
.
1. Если звено совершает только вращательное движение, то его кинетическая энергия равна: 
для кривошипов, кулис коромысел.
2. Если звено совершает только поступательное движение: 
для ползуна.
3. Сложное движение: 
для ползуна.
Кинетическая энергия всего механизма: 
k – номер подвижного звена; n – число звеньев.
Определение кинетической энергии, для кривошипно-ползунного механизма.
.
Приведённый момент инерции механизма.
Приведение масс основано на равенстве кинетических энергий реальных звеньев и звена приведения (начальный механизм).
; 
.
.
При динамическом исследовании механизма на расчётной схеме машинного агрегата отмечают основные силовые факторы и основные массы звена. Затем осуществляют переход от расчётной схемы одномассовой динамической модели. При переходе за звено приведения.
В дальнейшем: 
момент инерции звена относительно ц.т. 
; 
, 
приведённые к начальному звену моменты инерции всех подвижных звеньев .
приведённая к начальному звену машины работа движущих сил в интервале от i-го g i+1 положения, 
.
приведённая к начальному звену работа сил полезного сопротивления, сил веса подвижных звеньев машины, сил трения в рассматриваемом интервале, .
