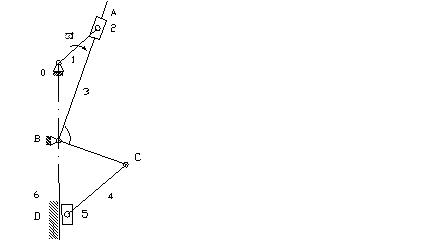
В первую очередь следует:
1. поставить шарниры;
2. пронумеровать звенья.
6 – 1 НКП – вращательная (в сложном шарнире кинематических пар на одну меньше);
1 – 2 НКП – вращательная;
2 – 3 НКП – поступательная;
3 – 6 НКП – вращательная;
3 – 4 НКП – вращательная;
4 – 5 НКП – вращательная;
5 – 6 НКП – поступательная.
Wф = 1 – фактическая степень свободы;
Wч = 3(n – 1) – 2Pн – Рв = 1;
qм = Wф – Wч, следовательно qм = 0.
Структурный анализ механизма:
1. Ищем начальный механизм
НМ – 6 – 1 
2. Ищем возможные поводки
1ая2ПГ→2, 3→3го вида 
2ая2ПГ→4, 5→2го вида 
3. Построить характерные точки
Кинематика структурных групп.
Два способа разложения движения
I способ.
Первый способ применяют в том случае, когда известно движение одной точки звена и необходимо определить движение другой точки этого же звена.
; 
; 
;
, 
; 
; 
; 
; 
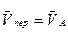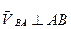
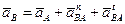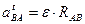
II способ.
Второй способ разложения движения применяют тогда, когда известно движение точки одного звена и необходимо определить движение точки другого звена, составляющего с первым звеном поступательную пару.
; 
; 
, 
; 
; 
, 
.
; 
; 
; 
.
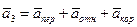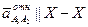Для плоского механизма 
= 1, т.к. угол между векторами = 
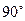
Кинематика двух поводковой группы первого вида.
В дальнейшем принято величину, известную по модулю и направлению, подчёркивать двумя чертами. Если известна только линия действия вектора, то его подчёркивают одной чертой и указывают направление. При этом символ «||» обозначает параллельность, а «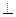
» - перпендикуляпрость к линии.
Абсолютную линейную скорость и ускорение любой точки можно представить в виде геометрической суммы переносного и относительных движений. За переносное движение принимают заданное движение (Va, aA) и его считают поступательным движением. Относительным движением исследуемой точки В является вращательное движение этой точки относительно заданной точки А. Это движение известно только по направлению.
где:
Vпер, VА – скорость переносного движения, м/с;
Vотн, VВА – скорость относительного движения, м/с;
, 
– ускорение переносного движения, м/с2;
, 
- нормальная составляющая ускорения относительного движения. Это ускорение направленно от исследуемой точки В к заданной точке А по прямой линии. Оно определяется: 
, где 
– угловая скорость звена, с-1; 
– длина звена.
, 
– тангенциальная составляющая ускорения относительного движения, м/с2. Это ускорение направлено по касательной к исследуемой точки В, т.е. перпендикулярна прямой АВ. Оно определяется как 
– угловое ускорение звена, с-2.
В этом случае абсолютное движение исследуемой точки раскладывают на переносное движение (совместное движение ползуна и направляющей) и на относительное движение (движение ползуна по направляющей). Переносное движение считается поступательным и равным движению заданной точки (А2). Относительное движение исследуемой точки направленно по направляющей.
4 – 1 НКП – вращательная
1 – 2 НКП – вращательная
2 – 3 НКП - вращательная
3 – 4 НКП - вращательная
Wф = 1 – фактическая степень свободы
Wч = 3(n – 1) – 2Pн = 1
qм = Wф – Wч, следовательно qм = 0
Н. М.: 4 – 1 (О, А1)
1ая 2ПГ→1го вида
ω1 = const, VA1 = ω1ROA, 
, 
, 
.
Планом скоростей (ускорений) – называется чертёж, на котором в определённом масштабе нанесены векторы скоростей (ускорений) основных точек механизма.
Построение плана скоростей
; 
, 
, 
; 
. 
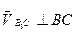
- масштабный коэффициент плана механизма. 
; 
.
Берут произвольную точку Р (полюс плана), от неё по направлению вращения ω1 откладывают отрезок Р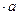 
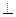ОА. Это скорость точки А на начальном звене, затем вычисляют масштабный коэффициент скорости 
, строят план скоростей.
; 
.
; 
Направление ω2 и ω3 совпадает с 
, 
Построение плана ускорений.
; 
, 
, 
; 
, 
, 
; 
; 
; 
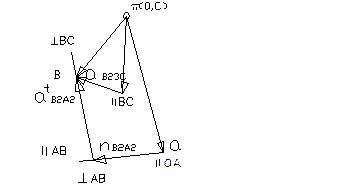
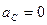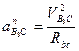В этом выражении известно ускорение 
, нормальные составляющие 
и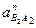 
, тангенциальные составляющие 
и 
известны только по направлению. Строят план ускорений. Отмечают точку П и из неё параллельно звену ОА проводят прямую линию. Нормальное ускорение точки А направленно к центру вращения. От точки П по направлению откладываем отрезок ПА производной длины. Этот отрезок будет соответствовать ускорению точки А, затем вычисляем масштабный коэффициент и отрезок нормального ускорения и .
; 
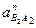. (мм);
, (мм)
Строим план ускорений.
Отрезок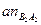 
направлен от точки В к точке А, центру относительного движения точки В. Отрезок 
направлен от точки В к точке С, центру относительного движения точки В. Точка b является точкой пересечения линий действия тангенциальных ускорений и . Для определения реальных значений ускорений 
, , необходимо соответствующие длины отрезков на плане ускорений умножить на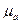 
:
; 
; 
Для расчёта условных звеньев 2 и 3 необходимо тангенциальные ускорения и разделить на соответствующие длины звеньев.
;
;
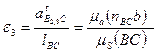направление угловых ускорений совпадает с направлениями тангенциальных ускорений.
