Краткие теоретические сведения. В предыдущей лабораторной работе рассматривалась цепь, в одной из параллельных ветвей которой включен идеальный конденсатор (его активное сопротивление

В предыдущей лабораторной работе рассматривалась цепь, в одной из параллельных ветвей которой включен идеальный конденсатор (его активное сопротивление принималось равным нулю). В данной работе предлагается цепь (рис. 58), в которой в каждой параллельной ветви имеются активные и реактивные элементы, такую цепь называют цепью с реальными элементами.

 

Рисунок 58 – Схема электрической параллельной цепи с реальными элементами

 

Условие резонанса токов для этой цепи b_L = b_C, где

 

b_L= ; b_C = , (11.1)

 

= . (11.2)

 

Решая это равенство относительно частоты «ω», получим

 

ω = . (11.3)

 

Учитывая, что соотношение является собственной частотой резонансного контура ω₀, а есть волновое или характеристическое сопротивление ρ, окончательное выражение для резонансной частоты:

 

ω = (11.4)

 

Из последнего выражения можно сделать следующие выводы:

– резонанс в цепи с реальными элементами зависит не только от L, C и ω, но, в отличие от резонанса напряжений, еще и от активных сопротивлений параллельных ветвей R₁ и R₂;

– возможность установления резонанса токов зависит от соотношения активных сопротивлений ветвей R₁ и R₂ и характеристического – ρ.

Всего имеется 4 варианта соотношения ρ с R₁ и R₂, которые и устанавливают 4 возможных резонансных режима.

Вариант 1. Если R₁ > ρ и R₂ > ρ или R₁ < ρ и R₂ < ρ, то для резонансной частоты ω = k ω₀, т. е. резонанс токов возможен на частоте, кратной собственной.

Вариант 2. Если R₁ = R₂ ≠ ρ, то соотношение для резонансной частоты ω имеет вид:

 

ω_р = ω₀, (11.5)

 

т. е. резонанс токов возможен на частоте, равной собственной.

Вариант 3. Если R₁ = R₂ = ρ, и соотношение для ω

 

ω_р = ω₀ 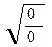, (11.6)

 

Раскрывая неопределенность любым известным способом, получают значение резонансной частоты

 

ω = 0 ÷ ∞, (11.7)

 

т. е. резонанс токов может наблюдаться на любой частоте в диапазоне от 0 до бесконечно большого значения, причем на любой из частот соблюдается равенство реактивных токов параллельных ветвей I_L = I_C. Пояснения и доказательства этого равенства изложены в лекционном материале, студентам необходимо с ними ознакомиться.

Вариант 4. Если R₁ > ρ, а R₂< ρ или R₁< ρ и R₂> ρ, выражение для ω имеет вид:

 

ω = j k ω₀, (11.8)

 

т. е. это вариант мнимого резонанса, он не может возникнуть на любой из частот.

Зависимость проводимостей (или сопротивлений) электрических цепей от частоты называют частотными характеристиками. Нас в этой работе интересуют частотные индуктивная b_L(ω) и емкостная b_C(ω) характеристики:

 

b_L = ; b_C = . (11.9)

 

Такие характеристики легко получить с помощью ПЭВМ. Графики этих зависимостей приведены на рисунке 59.

 

 

Рисунок 59 – Графики частотных характеристик: индуктивной b_L(ω)

и емкостной b_C (ω)

 

Обе функции имеют одинаковый характер.

Анализ этих характеристик показывает, что обе проводимости при ω=0 равны нулю, при увеличении частоты ω→ ∞ эти функции также стремятся к нулю.

Исследование на экстремум этих функций дает значение частоты, при которой b_L (ω) и b_C (ω) равны максимуму: b_Lmax – при ω= ; b_Cmax – при ω = .

В случае безразличного резонанса обе функции имеют одновременный максимум при частоте ω = .

Лабораторная работа выполняется на ПЭВМ и сводится к исследованию влияния активных сопротивлений R₁ и R₂ на условие резонанса и величину резонансной частоты.

Для оценки результатов рассматриваются зависимости b_L(ω), b_C(ω), I(ω), φ(ω). Полученные графики анализируются и делаются подробные выводы.