Якщо при побудові ПЛКРМ методом найменших квадратів виконуються усі припущення класичного кореляційно-регресійного аналізу, то параметри 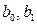 є величинами, які розподілені за нормальним законом.
є величинами, які розподілені за нормальним законом.
Параметри нормального закону розподілу випадкових величин 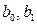 невідомі. Якщо замість дисперсії випадкових величин
невідомі. Якщо замість дисперсії випадкових величин 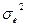 взяти її оцінку
взяти її оцінку 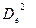 , то формули для оцінки дисперсій b0 i b1:
, то формули для оцінки дисперсій b0 i b1:
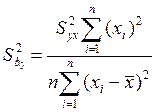
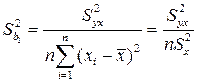
Стандартною вибірковою похибкою b0 ПЛКРМ називають величину:
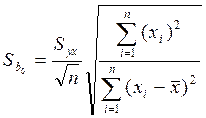
На підставі стандартної похибки при заданому значенні довірчої ймовірності р можна знайти граничну похибку b0 та побудувати довірчий інтервал для істинного значення параметра 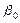 узагальненої ПЛКРМ:
узагальненої ПЛКРМ:
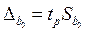
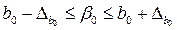
Геометрично довірчий інтервал інтерпретується парою паралельних прямих, між початковими координатами яких з довірчою ймовірністю р знаходиться істинне значення параметра 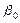 ПЛКРМ:
ПЛКРМ:
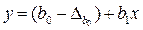
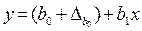
Стандартною вибірковою похибкою коефіцієнта регресії b0 ПЛКРМ:
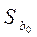 = 39995,6
= 39995,6
tp =1,714 (користуємося таблицями розподілу Стьюдента), тоді:
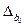 = 1,714 * 39995,6= 68552,46
= 1,714 * 39995,6= 68552,46
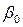 :
: 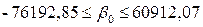
Таблиця 14.1. Значення вибіркових похибок параметра регресії β0
| Регіон | ỹ-68552,46 | ỹ | ỹ+68552,46 |
| АР Крим | -38090,29 | 30462,17 | 99014,63 |
| Вінницька | -51071,55 | 17480,91 | 86033,37 |
| Волинська | -58407,00 | 10145,46 | 78697,92 |
| Дніпропетровська | -4838,40 | 63714,06 | 132266,52 |
Продовження таблиці 14.1. Значення вибіркових похибок параметра регресії β0
| Донецька | 12917,07 | 81469,53 | 150021,99 |
| Житомирська | -56963,41 | 11589,05 | 80141,51 |
| Закарпатська | -57921,92 | 10630,54 | 79183,00 |
| Запорізька | -34804,74 | 33747,72 | 102300,18 |
| Івано-Франківська | -53677,46 | 14875,00 | 83427,46 |
| Київська | -43673,32 | 24879,14 | 93431,60 |
| Кіровоградська | -61079,71 | 7472,75 | 76025,21 |
| Луганська | -39949,76 | 28602,70 | 97155,16 |
| Львівська | -35607,52 | 32944,94 | 101497,40 |
| Миколаївська | -53741,84 | 14810,62 | 83363,08 |
| Одеська | -27317,38 | 41235,08 | 109787,54 |
| Полтавська | -50342,21 | 18210,25 | 86762,71 |
| Рівненська | -59439,75 | 9112,71 | 77665,17 |
| Сумська | -58572,59 | 9979,87 | 78532,33 |
| Тернопільська | -61537,84 | 7014,62 | 75567,08 |
| Харківська | -10077,76 | 58474,70 | 127027,16 |
| Херсонська | -57149,72 | 11402,74 | 79955,20 |
| Хмельницька | -54643,20 | 13909,26 | 82461,72 |
| Черкаська | -55772,52 | 12779,94 | 81332,40 |
| Чернівецька | -62536,58 | 6015,88 | 74568,34 |
| Чернігівська | -59600,10 | 8952,36 | 77504,82 |
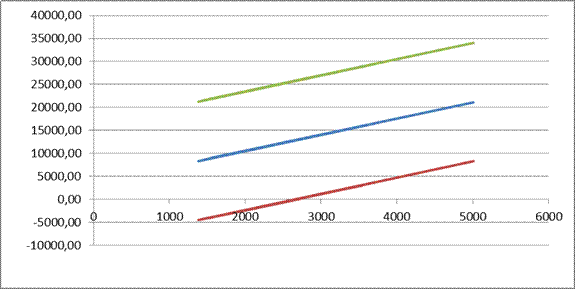
Рис. 14.1. Геометрична інтерпретація довірчого інтервалу для істинного значення β0
З ймовірністю 95% фактичне значення параметра 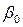 є між початковим ординатами цих прямих.
є між початковим ординатами цих прямих.
Стандартна похибка оцінки коефіцієнта регресії B1 обчислюється за формулою:
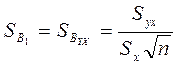
Гранична похибка оцінки коефіцієнта регресії B0 обчислюється за формулою:
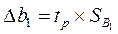
Геометрично довірчий інтервал інтерпретується парою прямих, що перетинаються у точці 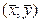 :
:
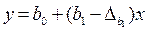
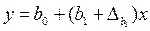
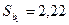
tp =1,714 (користуємося таблицями розподілу Стьюдента), тоді:
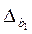 = 1,714 * 2,22= 3,81
= 1,714 * 2,22= 3,81
З ймовірністю 95% фактичне значення параметра b1 належить цьому проміжку:
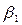 :
: 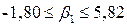
Таблиця 14.2. Значення вибіркових похибок параметра регресії β1
| Регіон | ỹ- 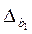 x x
| ỹ | ỹ+ 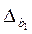 x x
|
| АР Крим | 11949,20 | 30462,17 | 11582,67 |
| Вінницька | 12720,72 | 17480,91 | 7406,82 |
| Волинська | 12365,20 | 10145,46 | 9331,07 |
| Дніпропетровська | 10055,12 | 63714,06 | 21834,38 |
| Донецька | 10663,28 | 81469,53 | 18542,71 |
| Житомирська | 13294,00 | 11589,05 | 4303,94 |
| Закарпатська | 13180,08 | 10630,54 | 4920,53 |
| Запорізька | 11974,96 | 33747,72 | 11443,24 |
| Івано-Франківська | 11786,00 | 14875,00 | 12465,99 |
| Київська | 7702,16 | 24879,14 | 34569,77 |
| Кіровоградська | 12659,92 | 7472,75 | 7735,90 |
| Луганська | 11537,68 | 28602,70 | 13810,02 |
| Львівська | 11573,36 | 32944,94 | 13616,90 |
| Миколаївська | 12411,76 | 14810,62 | 9079,06 |
| Одеська | 11296,24 | 41235,08 | 15116,82 |
| Полтавська | 9782,32 | 18210,25 | 23310,91 |
| Рівненська | 12681,36 | 9112,71 | 7619,85 |
| Сумська | 13503,12 | 9979,87 | 3172,08 |
| Тернопільська | 13101,36 | 7014,62 | 5346,60 |
| Харківська | 11367,12 | 58474,70 | 14733,18 |
| Херсонська | 12505,36 | 11402,74 | 8572,45 |
| Хмельницька | 12025,20 | 13909,26 | 11171,32 |
| Черкаська | 11701,52 | 12779,94 | 12923,24 |
| Чернівецька | 12558,48 | 6015,88 | 8284,94 |
| Чернігівська | 12905,52 | 8952,36 | 6406,59 |
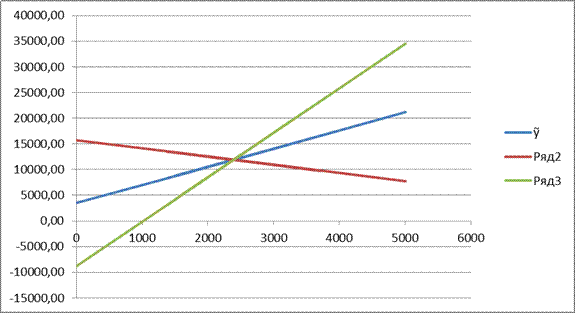
Рис. 14.2. Геометрична інтерпретація довірчого інтервалу для істинного значення β1






