Чтобы показать несчётность всего множества вещественных чисел, достаточно показать несчётность интервала 
.[18]
Пусть все числа указанного промежутка уже занумерованы некоторым образом. Тогда их можно выписать в следующем виде:
Здесь aij — j -я цифра i -ого числа. Очевидно, что все числа указанного вида действительно принадлежат рассматриваемому промежутку, если только в каждом числе не все цифры сразу являются нулями или девятками.
Далее предлагается рассмотреть следующее число:
Пусть каждая цифра di этого числа удовлетворяет следующим трём свойствам:
§ 
§ 
§ 
Такое число действительно существует на указанном промежутке, так как оно является вещественным, не совпадает ни с нулём, ни с единицей, а десятичных цифр достаточно, чтобы третье свойство выполнялось. Кроме этого, x интересно тем фактом, что оно не совпадает ни с одним из чисел xj, выписанных выше, ведь иначе j -я цифра числа x совпала бы с j -ой цифрой числа xj. Пришли к противоречию, заключающемуся в том, что как бы числа рассматриваемого промежутка ни были занумерованы, всё равно найдётся число из этого же промежутка, которому не присвоен номер.[18]
Это свидетельствует о том, что множество вещественных чисел не является счётным. Его мощность называется мощностью континуума.
Расширенная числовая прямая 
(читается «эр с чертой») — множество вещественных чисел 
, дополненное двумя элементами: 
(положительная бесконечность) и 
(отрицательная бесконечность), то есть
Бесконечности и , которые не являются числами в обычном понимании этого слова, также называют бесконечными числами, в отличие от вещественных чисел 
, называемых конечными числами. При этом для любого вещественного числа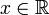 
по определению полагают выполненными неравенства
Cледует отличать расширенную числовую прямую от множества вещественных чисел, дополненного одной бесконечностью 
. Такая система называется проективной прямой, и обозначается 
Множество вещественных чисел линейно упорядоченно по отношению 
. Однако в нет максимального и минимального элементов. Если рассматривать систему вещественных чисел как линейно упорядоченное множество, то ее расширение до системы как раз состоит в добавлении максимального () и минимального () элементов.
Благодаря этому, в системе всякой непустое множество имеет точную верхную грань (конечную, если множество ограничено сверху, и , если не ограничено сверху). Аналогичное утверждение справедливо и для точной нижней грани. Этим объясняется удобство введения элементов и .
Билет 16 вопрос 1
Системное проектирование
К концу 20 века не только существенно возросла сложность проектируемых объектов, но и их воздействие на общество и окружающую среду, тяжкость последствий аварий из-за ошибок разработки и эксплуатации, высокие требования к качеству и цене, сокращению сроков выпуска новой продукции. Необходимость учета этих обстоятельств заставляла вносить изменения в традиционный характер и методологию проектной деятельности.
При создании объектов их уже необходимо было рассматривать в виде систем, то есть комплекса взаимосвязанных внутренних элементов с определенной структурой, широким набором свойств и разнообразными внутренними и внешними связями. Сформировалась новая проектная идеология, получившая название системного проектирования.
Системное проектирование комплексно решает поставленные задачи, принимает во внимание взаимодействие и взаимосвязь отдельных объектов-систем и их частей как между собой, так и с внешней средой, учитывает социально-экономические и экологические последствия их функционирования. Системное проектирование основывается на тщательном совместном рассмотрении объекта проектирования и процесса проектирования, которые в свою очередь включают ещё ряд важных частей, показанных на рисунке 1.
