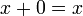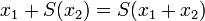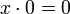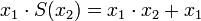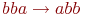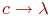Билет 1 вопрос 1
ПРОЕКТИРОВАНИЕ - процесс составления описания, необходимого для создания в заданных условиях еще не существующего объекта, на основе первичного описания этого объекта и (или) алгоритма его функционирования или алгоритма процесса преобразованием (в ряде случаев неоднократным) первичного описания, оптимизацией заданных характеристик объекта и алгоритма его функционирования или алгоритма процесса, устранением некорректности первичного описания и последовательным представлением (при необходимости) описаний на различных языках (ГОСТ-22487-77). Если подходить с глобальной позиции жизненного цикла технической системы, то проектирование является одной из его наиболее важных частей. Такое соотношение показано на рис.1.
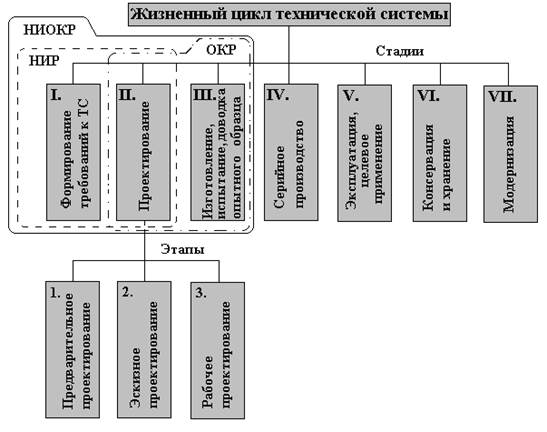
Рис. 1. Проектирование как часть жизненного цикла технической системы
Лишь тогда, когда определен объект проектирования, можно говорить о каком-либо маршруте проектирования, который бы был достаточно специфичен по отношению к этому объекту, но с другой стороны, обладал бы достаточной универсальностью. Важно также отметить, что в применении к ИМС традиционно возникает проблема разделения/общности непосредственно схемотехнического проектирования и физико-технологического проектирования, в связи с чем получило развитие понятие «приборно-технологического базиса».
Билет 1 вопрос 2
Аксио́мы Пеа́но — одна из систем аксиом для натуральных чисел.
Аксиомы Пеано позволили формализовать арифметику. После введения аксиом стали возможны доказательства многих свойств натуральных и целых чисел, а также использование целых чисел для построения формальных теорий рациональных и вещественных чисел.
О неполноте
Как следует из теоремы Гёделя о неполноте, существуют утверждения о натуральных числах, которые нельзя ни доказать, ни опровергнуть, исходя из аксиом Пеано. Некоторые такие утверждения имеют достаточно простую формулировку, например, теорема Гудстейна.
Теоре́ма Гёделя о неполноте́ и втора́я теоре́ма Гёделя [~ 1] — две теоремы математической логики о принципиальных ограничениях формальной арифметики и, как следствие, всякой формальной системы, в которой можно определить основные арифметические понятия: натуральные числа, 0, 1, сложение и умножение.
Первая теорема утверждает, что если формальная арифметика непротиворечива, то в ней существует невыводимая и неопровержимая формула.
Вторая теорема утверждает, что если формальная арифметика непротиворечива, то в ней невыводима некоторая формула, содержательно утверждающая непротиворечивость этой теории.
Эти теоремы были доказаны Куртом Гёделем в 1930 году (опубликованы в 1931) и имеют непосредственное отношение ко второй проблеме из знаменитого списка Гильберта.
Формулировки
Словесная
- 1 является натуральным числом;
- Число, следующее за натуральным, также является натуральным;
- 1 не следует ни за каким натуральным числом;
- Если натуральное число
 непосредственно следует как за числом
непосредственно следует как за числом  , так и за числом
, так и за числом  , то
, то  и
и  тождественны;
тождественны; - (Аксиома индукции) Если какое-либо предложение доказано для 1 (база индукции) и если из допущения, что оно верно для натурального числа
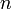 , вытекает, что оно верно для следующего за
, вытекает, что оно верно для следующего за 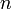 натурального числа (индукционное предположение), то это предложение верно для всех натуральных чисел.
натурального числа (индукционное предположение), то это предложение верно для всех натуральных чисел.
Математическая
Введём функцию 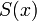 , которая сопоставляет числу
, которая сопоставляет числу 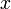 следующее за ним число.
следующее за ним число.
-
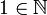 ;
; -
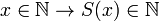 ;
; -
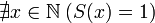 ;
; -
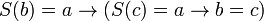 ;
; -
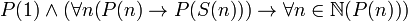 .
.
Или так:
-
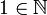 ;
; -
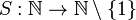 ;
; -
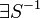 ;
; -
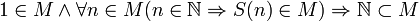 .
.
Дословный текст
Текст аксиом Пеано, как он приведен в оригинальном издании Пеано.
- «1 есть натуральное число»;
- «следующее за натуральным числом есть натуральное число»;
- «1 не следует ни за каким натуральным числом»;
- «всякое натуральное число следует только за одним натуральным числом»;
- Аксиома полной индукции.
Формализация арифметики
Формализация арифметики включает в себя аксиомы Пеано, а также вводит число 0 и операции сложения и умножения с помощью следующих аксиом:
Билет 2 вопрос 1
Билет 2 вопрос 1

Билет 2 вопрос 2
Основна́я теоре́ма арифме́тики утверждает:
Каждое натуральное число n > 1 представляется в виде 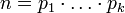 , где
, где 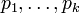 — простые числа, причём такое представление единственно с точностью до порядка следования сомножителей.
— простые числа, причём такое представление единственно с точностью до порядка следования сомножителей.
Единицу можно также считать произведением нулевого количества простых чисел, «пустым произведением».
Как следствие, каждое натуральное число n единственным образом представимо в виде
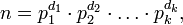 где
где 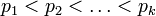 — простые числа, и
— простые числа, и 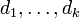 — некоторые натуральные числа.
— некоторые натуральные числа.
Такое представление числа n называется его каноническим разложением на простые сомножители.
Следствия
Основная теорема арифметики даёт элегантные выражения для наибольшего общего делителя и наименьшего общего кратного.
Доказательство
Доказательство основной теоремы арифметики опирается на лемму Евклида:
Если простое число p делит без остатка произведение двух целых чисел 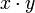 , то p делит x или y. , то p делит x или y.
|
Существование. Пусть n — наименьшее натуральное число, неразложимое в произведение простых чисел. Оно не может быть единицей по формулировке теоремы. Оно не может быть и простым, потому что любое простое число является произведением одного простого числа — себя. Если n составное, то оно — произведение двух меньших натуральных чисел. Каждое из них можно разложить в произведение простых чисел, значит, n тоже является произведением простых чисел. Противоречие.
Единственность. Пусть n — наименьшее натуральное число, разложимое в произведение простых чисел двумя разными способами. Если оба разложения пустые — они одинаковы. В противном случае, пусть p — любой из сомножителей в любом из двух разложений. Если p входит и в другое разложение, мы можем сократить оба разложения на p и получить два разных разложения числа n / p, что невозможно. А если p не входит в другое разложение, то одно из произведений делится на p, а другое — не делится (как следствие из леммы Евклида, см. выше), что противоречит их равенству.
Вели́кая теоре́ма Ферма́ (или Последняя теорема Ферма) — одна из самых популярных теорем математики; её условие формулируется на понятийном уровне среднего общего образования, а доказательство теоремы искали многие математики более трёхсот лет. Окончательно доказана в 1995 году Эндрю Уайлсом.
Теорема утверждает, что:
Для любого натурального числа n > 2 уравнение
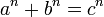 не имеет натуральных решений a, b и c.
не имеет натуральных решений a, b и c.
|
Ма́лая теоре́ма Ферма́ — классическая теорема теории чисел, которая утверждает, что
| Если p — простое число, и целое a не делится на p, то a p − 1 ≡ 1 (mod p) (или a p − 1 − 1 делится на p). |
Иная формулировка:
| Для любого простого p и целого a, (a p − a) делится на p. |
Обобщения теоремы
- Если p простое число, а m и n — такие положительные целые числа, что
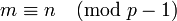 , тогда
, тогда 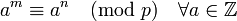 . Это утверждение используется в системе шифрования с открытым ключом RSA.
. Это утверждение используется в системе шифрования с открытым ключом RSA. - Малая теорема Ферма является частным случаем теоремы Эйлера, которая, в свою очередь, является частным случаем теорем Кармайкла и Лагранжа.
- Малая теорема Ферма также имеет изящное обобщение в теории конечных полей.
·
Теоре́ма Э́йлера в теории чисел гласит:
Если a и m взаимно просты, то 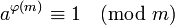 , где φ(m) — функция Эйлера. , где φ(m) — функция Эйлера.
|
Функция Эйлера φ(n), где n — натуральное число, равна количеству натуральных чисел, меньших n и взаимно простых с ним
Целые числа называются взаимно простыми, если они не имеют никаких общих делителей, кроме ±1.
Теорема о распределении простых чисел — теорема аналитической теории чисел, описывающая асимптотику распределения простых чисел. А именно, она утверждает, что количество π(n) простых чисел на отрезке от 1 до n растёт с ростом n как 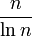 , то есть:
, то есть:
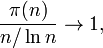 когда
когда 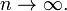
Грубо говоря, это означает, что у случайно выбранного числа от 1 до n шанс оказаться простым примерно равен 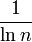 .
.
Также эта теорема может быть эквивалентным образом переформулирована для описания поведения k -го простого числа pk: она утверждает, что
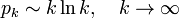
(здесь и далее запись 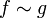 означает:
означает: 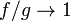 ).
).
Билет 3 вопрос 1
| Аспект Уровень | Поведенческая область | Структурная область | Физическая область |
| Архитектурный уровень | Спецификации | Процессор, память, переключатели, контроллеры | Физическая декомпозиция |
| Алгоритмический уровень (или уровень транзакций) | Алгоритмы | Функциональные блоки | Кластеры |
| Уровень функциональных блоков | Регистровые передачи | АЛУ, регистры | Планирование кристалла |
| Логический уровень | Булевы уравнения | Триггеры, ключи | Ячейки |
| Схемотехнический уровень | Дифференциальные уравнения | Транзисторы | Компоненты ячеек |
| Физико-топологический (компонентный) уровень | Уравнения математической и теоретической физики | Элементарные структуры | Компоненты транзисторов |
Табл. 1. Уровни и аспекты проектирования
Уровни проектирования
- Логический — логическая схема (логические инверторы, элементы ИЛИ-НЕ, И-НЕ и т. п.).
- Схемо- и системотехнический уровень — схемо- и системотехнические схемы (триггеры, компараторы, шифраторы, дешифраторы, АЛУ и т. п.).
- Электрический — принципиальная электрическая схема (транзисторы, конденсаторы, резисторы и т. п.).
- Физический — методы реализации одного транзистора (или небольшой группы) в виде легированных зон на кристалле.
- Топологический — топологические фотошаблоны для производства.[Прим. 1]
- Программный уровень — позволяет программисту программировать (для ПЛИС, микроконтроллеров и микропроцессоров) разрабатываемую модель используя виртуальную схему.
Билет 4 вопрос 1
Казёнов страница 82
Билет 4 вопрос 2
Для определения НАМ вводится произвольный алфавит - конечное непустое множество символов, при помощи которых описывается алгоритм и данные. В алфавит также включается пустой символ, который мы будем обозначать греческой буквой 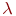 . Под словом понимается любая последовательность непустых символов алфавита либо пустой символ, который обозначает пустое слово.
. Под словом понимается любая последовательность непустых символов алфавита либо пустой символ, который обозначает пустое слово.
Всякий НАМ определяется конечным упорядоченным множеством пар слов алфавита, называемых подстановками. В паре слов подстановки левое (первое) слово непустое, а правое (второе) слово может быть пустым символом. Для наглядности левое и правое слово разделяются стрелкой. Например,
В качестве данных алгоритма берется любая непустая строка символов. Работа НАМ состоит из последовательности совершенно однотипных шагов. Шаг работы алгоритма может быть описан следующим образом:
- В упорядоченной последовательности подстановок ищем самую первую подстановку, левое слово которой входит в строку данных.
- В строке данных ищем самое первое (левое) вхождение левого слова найденной подстановки.
- Это вхождение в строке данных заменяем на правое слово найденной подстановки (преобразование данных).
Шаг работы алгоритма повторяется до тех пор, пока
- либо не возникнет ситуация, когда шаг не сможет быть выполнен из-за того, что ни одна подстановка не подходит (левое слово любой подстановки уже не входит в строку данных) - правило остановки;
- либо не будет установлено, что процесс подстановок не может остановиться.
В первом случае строка данных, получившаяся при остановке алгоритма, является выходной (результатом) и алгоритм применим к входным данным, а во втором случае алгоритм не применим к входным данным.
Так, определенный выше в примере нормальный алгоритм Маркова преобразует слово 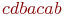 в слово
в слово 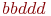 следующим образом (над стрелкой преобразования мы пишем номер применяемой подстановки, а в преобразуемой строке подчеркиваем левое слово применяемой подстановки):
следующим образом (над стрелкой преобразования мы пишем номер применяемой подстановки, а в преобразуемой строке подчеркиваем левое слово применяемой подстановки):
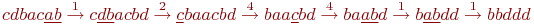 ,
,
а при преобразовании слова abbc этот же алгоритм будет неограниченно работать, так как имеет место цикличное повторение данных:

Таким образом, всякий нормальный алгоритм Маркова определяет функцию, которую мы назовем нормальной (или вычислимой по Маркову), которая может быть частичной и которая в области определения входному слову ставит в соответствие выходное слово.
Пример 2. Прежде, чем перейти к другим арифметическим операциям, рассмотрим как довольно типичный пример, используемый часто в других алгоритмах, алгоритм копирования двоичного числа. В этом случае прежде всего исходное и скопированное числа разделим символом "*". В разрабатываемом алгоритме мы будем копировать разряды числа по очереди, начиная с младшего, но нужно решить 2 проблемы: как запоминать значение символа, который мы копируем, и как запоминать место копируемого символа. Для решения второй проблемы используем символ "!", которым мы будем определять еще не скопированный разряд числа, после которого и стоит этот символ. Для запоминания значения копируемого разряда мы будем образовывать для значения 0 символ "a", а для значения 1 - символ "b". Меняя путем подстановок эти символы "a" или "b" с последующими, мы будем передвигать разряды "a" или "b" в начало копируемого числа (после "*"), но для того, чтобы пока не происходило копирование следующего разряда справа, мы перед передвижением разряда временно символ "!" заменим на символ "?", а после передвижения сделаем обратную замену. После того как все число окажется скопированным в виде символов "a" и "b", мы заменим эти символы на 0 и 1 соответственно. В результате нормальный алгоритм копирования двоичного числа можно определить следующей последовательностью подстановок:

Продемонстрируем работу алгоритма для числа 10:
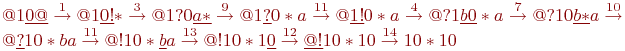
Билет 5 вопрос 1
Казёнов страница 84
Билет 6 вопрос 1
сквозное проектирование предполагает наличие единой системы конструкторской документации (ЕСКД). Смысл сквозной технологии состоит в эффективной передаче данных и результатов конкретного текущего этапа проектирования сразу на все последующие этапы. Разработчику часто не хватает регламентированной информации от предыдущего этапа и необходима более полная и разнообразная информация, которая могла быть сформулирована на одном из ранних этапов проектирования (не обязательно на соседнем). У разработчиков, выполняющих различные этапы проектирования, может быть одновременно с первым этапом проектирования получено техническое задание и таким образом, все разработчики могут одновременно начать продумывать, как более успешно реализовать свой этап. Данная технология базируется на модульном построении САПР, на использовании общих баз данных и баз знаний, и характеризуется широкими возможностями моделирования и контроля на всех этапах проектирования. Сквозные САПР, как правило, являются интегрированными, т.е. имеют альтернативные алгоритмы реализации отдельных проектных процедур.
При параллельном проектировании информации относительно каких–либо промежуточных или окончательных характеристик разрабатываемого изделия формируется и предоставляется всем участникам работ, начиная с самых ранних этапов проектирования. В этом случае информация носит прогностический характер. Ее получение базируется на математических моделях и методах прогностической оценки критериев качества проектного решения. Оценка может производиться на основе аналитической модели, статистических методах и методах экспертных систем. Технология параллельного проектирования реализуется на основе интегрированных инструментальных средств прогностической оценки и анализа альтернативных проектных решений с последующим выбором базового проектного решения. Предполагается, что инженер начинает работать над проектом на высоком уровне абстракции с последующей детализацией проекта. Принципиальным отличием параллельного проектирования от сквозного проектирования (хотя параллельное проектирование получило развитие на основе сквозного) в том, что информация не просто поступает на все последующие этапы проектирования, но и по существу эти этапы начинают выполняться одновременно. Фирма MENTOR GRAPHICS впервые создала среду параллельного проектирования на основе принципа объединения всех инструментальных средств проектирования и данных в одном непрерывном и гибком процессе создания изделия.
Сквозное проектирование, если оно полностью автоматизировано, от получения ТЗ на создание технической системы до получения разводки печатной платы или, вообще говоря, до синтеза физической топологии «системы-в-корпусе» (System-on-Package, SiP) приводит нас к понятию «кремниевого компилятора» (silicon compiler, SC или КРК). Кремниевая компиляция значительно удешевляет и ускоряет проектирование СБИС, что позволяет реализовать поток заказов на проектирование специализированных СБИС. Появление термина «компилятор» объясняется определенным сходством процесса проектирования СБИС и разработки exe-кода прикладной программы, созданной для выполнения специальных задач. В таком широком понимании «кремниевый компилятор» является священным Граалем, по-видимому, недостижимым, инженерной науки. В узком понимании, предполагающем синтез топологии из некоторого описания прибора, уже имеется несколько вариантов SC. В 1984г. проф. Мид (Mead) анонсировал изготовление первого кремниевого компилятора. В СССР этой проблемой занимались А.Г.Марчук, З.В.Апанович и др. Примерно в 2000г. Белорусская Национальная академия наук также анонсировала создание своего SC.
Термин «кремниевый компилятор» был введен в 1979 г. для обозначения программной системы, осуществляющей получение топологии кристалла путем объединения параметризованных топологических ячеек. КРК различаются, во-первых, характером ограничений и условиями применения, во-вторых, широтой охвата проектных процедур и операций на маршруте проектирования СБИС. Большинство КРК являются специализированными – они проектируют СБИС конкретного типа, изготовляемые по конкретной технологии. В то же время качество схем, разработанных с помощью более универсальных КРК, оказывается ниже по ряду параметров и прежде всего по занимаемой площади кристалла. По широте охвата проектных процедур различают топологические системы и КРК, синтезирующие топологию на основе заданного поведенческого описания.
Билет 6 вопрос 2
Алгебраическая система или алгебраическая структура — множество G (носитель) с заданным на нём набором операций и отношений (сигнатура), удовлетворяющим некоторой системе аксиом. Понятие алгебраической системы родственно понятию универсальной алгебры.
n -арная операция на G — это отображение прямого произведения n экземпляров множества в само множество  . По определению, 0 -арная операция — это просто выделенный элемент множества. Чаще всего рассматриваются унарные и бинарные операции, поскольку с ними легче работать. Но в связи с нуждами топологии, алгебры, комбинаторики постепенно накапливается техника работы с операциями большей арности, здесь в качестве примера можно привести теорию операд (клонов полилинейных операций) и алгебр над ними (мультиоператорных алгебр).
. По определению, 0 -арная операция — это просто выделенный элемент множества. Чаще всего рассматриваются унарные и бинарные операции, поскольку с ними легче работать. Но в связи с нуждами топологии, алгебры, комбинаторики постепенно накапливается техника работы с операциями большей арности, здесь в качестве примера можно привести теорию операд (клонов полилинейных операций) и алгебр над ними (мультиоператорных алгебр).
Группоиды, полугруппы, группы
§ Группоид — множество с одной бинарной операцией 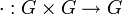 , обычно называемой умножением.
, обычно называемой умножением.
§ Правая квазигруппа — группоид, в котором возможно правое деление, то есть уравнение 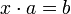 имеет единственное решение для любых a и b.
имеет единственное решение для любых a и b.
§ Квазигруппа — одновременно правая и левая квазигруппы.
§ Лупа — квазигруппа с единичным элементом 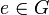 , таким, что
, таким, что 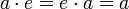 .
.
§ Полугруппа — группоид, в котором умножение ассоциативно: 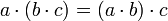 .
.
§ Моноид — полугруппа с единичным элементом.
§ Группа — моноид, в котором для каждого элемента a группы можно определить обратный элемент a −1, такой, что 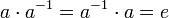 .
.
§ Абелева группа — группа, в которой операция коммутативна, то есть, 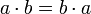 . Операцию в абелевой группе часто называют сложением ('+').
. Операцию в абелевой группе часто называют сложением ('+').
Кольца
§ Полукольцо — похоже на кольцо, но без обратимости сложения.
§ Почти-кольцо — также обобщение кольца, отличающееся от обычного кольца отсутствием требования коммутативности сложения и отсутствием требования дистрибутивности умножения по сложению (левой или правой)
§ Кольцо — структура с двумя бинарными операциями: абелева группа по сложению, моноид по умножению, выполняется закон дистрибутивности: 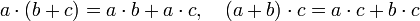 .
.
§ Коммутативное кольцо — кольцо с коммутативным умножением.
§ Целостное кольцо — кольцо, в котором произведение двух ненулевых элементов не равно нулю.
§ Тело — кольцо, в котором ненулевые элементы образуют группу по умножению.
§ Поле — коммутативное кольцо, являющееся телом.
Гру́ппа — непустое множество с определённой на нём бинарной операцией, удовлетворяющей указанным ниже аксиомам. Группы являются важными инструментами в изучении симметрии во всех её проявлениях. Примерами групп являютсявещественные числа с операцией сложения, множество вращений плоскости вокруг начала координат и т. п. Ветвь математики, занимающаяся группами, называется теорией групп.
Определения
Непустое множество G с заданной на нём бинарной операцией 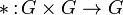 называется группой (G, *), если выполнены следующие аксиомы:
называется группой (G, *), если выполнены следующие аксиомы:
1. ассоциативность: 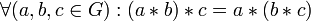 ;
;
2. наличие нейтрального элемента: 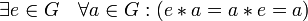 ;
;
3. наличие обратного элемента: 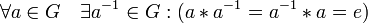
Править]Комментарии
§ Элемент a − 1, обратный элементу a, единственен.
§ В определении группы 2-ю и 3-ю аксиомы можно заменить одной аксиомой существования обратной операции:
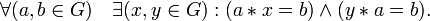
§ Вышеприведённые аксиомы не являются строго минимальными. Для существования нейтрального и обратного элементов достаточно наличия левого нейтрального (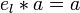 ) и левого обратного (
) и левого обратного (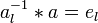 ) элементов. При этом они автоматически являются e и a − 1:
) элементов. При этом они автоматически являются e и a − 1:
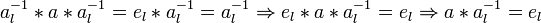
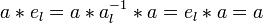
По́лем называется множество F с двумя бинарными операциями + (аддитивная операция, или сложение) и  (мультипликативная операция, или умножение), если оно (вместе с этими операциями) образует коммутативное ассоциативное кольцо c единицей
(мультипликативная операция, или умножение), если оно (вместе с этими операциями) образует коммутативное ассоциативное кольцо c единицей 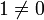 , все ненулевые элементы которого обратимы.
, все ненулевые элементы которого обратимы.
Иными словами, множество F с двумя бинарными операциями + (сложение) и  (умножение) называется полем, если оно образует коммутативную группу по сложению, все его ненулевые элементы образуют коммутативную группу по умножению, и выполняется свойстводистрибутивности.
(умножение) называется полем, если оно образует коммутативную группу по сложению, все его ненулевые элементы образуют коммутативную группу по умножению, и выполняется свойстводистрибутивности.
Связанные определения
§ Характеристика поля — наименьшее положительное целое число n такое, что сумма n копий единицы равна нулю:
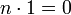
Если такого числа не существует, то характеристика равна 0 по определению.
§ Подполем поля k называется подмножество, которое само является полем относительно операций сложения и умножения, заданных в k. (Подполем поля k называется поле относительно операций умножения и сложения, заданных в k, несущим множеством которого является подмножество несущего множества k)
§ Расширение поля — поле, содержащее данное поле в качестве подполя.
§ Поле Галуа — поле, состоящее из конечного числа элементов.
§ Простое поле — поле, не содержащее собственных подполей.
Свойства
§ Характеристика поля всегда 0 или простое число.
§ Поле характеристики 0 содержит подполе, изоморфное полю рациональных чисел 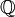 .
.
§ Поле простой характеристики p содержит подполе, изоморфное полю вычетов 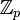 .
.
§ Количество элементов в конечном поле всегда равно pn — степени простого числа.
§ При этом для любого числа вида pn существует единственное (с точностью до изоморфизма) поле из pn элементов, обычно обозначаемое 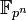 .
.
§ Любой ненулевой гомоморфизм полей является вложением.
§ В поле нет делителей нуля.