1. Метод последовательного дифференцирования применяется
для нахождения частного решения уравнения  , при начальных условиях
, при начальных условиях  ,
,  ,…,
,…,  (5.1),
(5.1),
удовлетворяющего теореме Коши о существовании и единственности решения. Решение ищется в виде ряда Тейлора 
 . (5.2)
. (5.2)
При этом часть коэффициентов известна из начальных условий, а следующие необходимые производные в точке  находятся при дифференцировании данного уравнения по
находятся при дифференцировании данного уравнения по  соответствующее число раз.
соответствующее число раз.
Этот метод не даёт возможности исследовать полученный ряд на сходимость. Однако он применим, когда заранее известно, что решение уравнения в виде ряда существует.
Пример 5.1. Найти первые пять членов разложения в степенной ряд решения уравнения  ,при начальных условиях
,при начальных условиях  ,
,  .
.
Решение будем искать в виде ряда (5.2):  . (5.3)
. (5.3)
Подставив в исходное уравнение начальные условия, найдём: 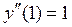 .
.
Дифференцируем по  заданное уравнение и находим следующие
заданное уравнение и находим следующие  :
:  ,
, 
 ,
, 
Теперь подставим данные значения в (5.3) и получим ответ:


Пример 5.2. Найти первые четыре члена разложения в степенной ряд решения уравнения  , при начальных условиях
, при начальных условиях 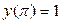 ,
, 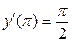 .
.
Вид решения:  (5.4)
(5.4)
Подставим в уравнение начальные условия: 
Дифференцируем данное уравнение и подставляем начальные условия: 
 ,
,  .
.
Окончательно, подставляя в (5.4) найденные значения  , получим Ответ:
, получим Ответ: 
2.Метод неопределённых коэффициентов удобен при решении линейных дифференциальных уравнений  с начальными условиями
с начальными условиями  ,
,  ,…,
,…,  .
.
Если коэффициенты уравнения 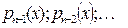 и
и 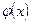 разложимы в степенные ряды по степеням
разложимы в степенные ряды по степеням  , сходящиеся в области
, сходящиеся в области 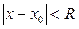 ,то уравнение имеет единственное решение
,то уравнение имеет единственное решение  в виде ряда
в виде ряда  , сходящегося в той же области.
, сходящегося в той же области.
Для нахождения коэффициентов  необходимо:
необходимо:
1)коэффициенты в уравнении 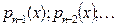 и
и  заменить их разложениями в ряды;
заменить их разложениями в ряды;
2)найти последовательно производные функции  ,
,
где коэффициенты  пока не определены, и подставить в исходное дифференциальное уравнение полученные разложения;
пока не определены, и подставить в исходное дифференциальное уравнение полученные разложения;
3) приравнивая коэффициенты при одинаковых степенях
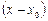 в правой и левой частях данного соотношения получить и решить систему уравнений относительно коэффициентов
в правой и левой частях данного соотношения получить и решить систему уравнений относительно коэффициентов  .Если найти конечное число коэффициентов
.Если найти конечное число коэффициентов  ,то получится приближённое решение.
,то получится приближённое решение.
Пример 5.3. Найти общее решение уравнения 
в окрестности точки  .
.
Решение ищем в виде ряда: 
Дифференцируя этот ряд, получим разложения для 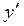 и
и  :
:
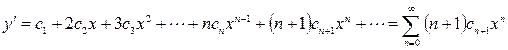

Подставим эти выражения для  ,
, 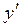 и
и 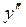 в исходное уравнение:
в исходное уравнение:
. 
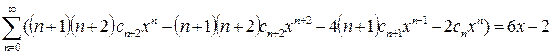
Приравнивая коэффициенты при одинаковых степенях  в обеих частях равенства, получим систему уравнений для нахождения
в обеих частях равенства, получим систему уравнений для нахождения 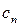 :
:


Следовательно, 
Подставляем найденные коэффициенты в разложение искомой функции:  =
= 
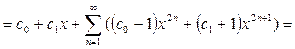

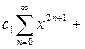

Исходное дифференциальное уравнение – линейное неоднородное второго порядка. Его общее решение должно иметь следующую структуру:  ,
,
где  и
и  - линейно независимые частные решения соответствующего однородного уравнения – они образуют фундаментальную систему решений,
- линейно независимые частные решения соответствующего однородного уравнения – они образуют фундаментальную систему решений, 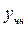 - частное решение данного неоднородного уравнения,
- частное решение данного неоднородного уравнения,  - общее решение соответствующего однородного уравнения.
- общее решение соответствующего однородного уравнения.
В полученном решении необходимая структура имеет место.
 ,
,  образуют фундаментальную систему решений соответствующего однородного уравнения.
образуют фундаментальную систему решений соответствующего однородного уравнения.
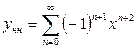 - частное решение неоднородного уравнения.
- частное решение неоднородного уравнения.
Учитывая, что в ответе присутствуют разложения известных функций (см.3.9)  , запишем полученное решение иначе:
, запишем полученное решение иначе:


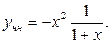
Ответ: 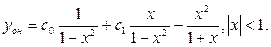
Пример 5.4. Найти частное решение уравнения  , при начальных условиях:
, при начальных условиях:  ,
,  .
.
Вычислить значение частного решения в точке 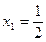 с точностью до δ=0,001.
с точностью до δ=0,001.
1. Представим решение в виде ряда  .
.
 ,
, 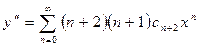 (см. пример 5.3).
(см. пример 5.3).
Разложив в ряд Маклорена cosx и sinx, получим после подстановки в уравнение следующее соотношение:


Подставляя начальные условия в разложения  и
и 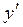 , находим:
, находим:  . Приравнивая коэффициенты при одинаковых степенях x слева и справа, получаем систему для нахождения остальных коэффициентов:
. Приравнивая коэффициенты при одинаковых степенях x слева и справа, получаем систему для нахождения остальных коэффициентов:
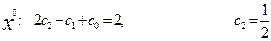 ,
,

 ,
,

 .
.
Просматривается закономерность:  ,
,  , n=0,1,2,…
, n=0,1,2,…
Проверим её, вычислив  и
и 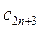 :
:
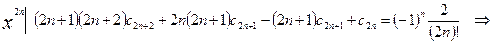
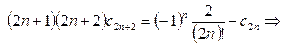

 .
.



Такие же 
 и получаются, если в выражения
и получаются, если в выражения 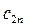 и
и 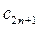 вместо n подставить n+1. Т.е. коэффициенты найдены верно.
вместо n подставить n+1. Т.е. коэффициенты найдены верно.
Искомое частное решение:  . Преобразуем его:
. Преобразуем его:

 =
= 
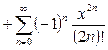 .
.
«Сместим» индекс суммирования первого ряда n→n+1:
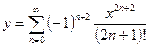
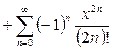

 .
.
Получили разложения известных функций (см. 3.4, 3.5).Перепишем решение иначе:  .
.
2. Чтобы вычислить приближённо значение полученного частного решения в точке 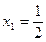 , подставим
, подставим  в наш ряд:
в наш ряд:  .
.
Этот знакочередующийся ряд удовлетворяет условиям теоремы Лейбница, поэтому, если заменить сумму S ряда частичной суммой  , то остаток ряда
, то остаток ряда 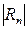 <
<  . Найдём несколько слагаемых:
. Найдём несколько слагаемых:  ,
,  ,
,  ,
,  .
.  . Погрешность
. Погрешность  . Ответ:
. Ответ:  ,
,  .
.
Контрольное задание.
1. Применяя метод последовательного дифференцирования, найти n первых членов разложения в степенной ряд решения дифференциального уравнения с заданными начальными условиями.
a)  ; b)
; b)  .
.
Ответ:a)  b)
b)  .
.
2. Применяя метод неопределённых коэффициентов, найти решение дифференциального уравнения, удовлетворяющее начальным условиям.
a)  ; b)
; b) 
Ответ: a)  ; b)
; b) 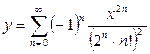 .
.
Содержание задания «Степенные ряды».
Задача 1. Найти интервал сходимости степенного ряда и исследовать сходимость ряда на концах этого интервала.
Задача 2. Пользуясь известными формулами разложения в степенной ряд функций  , разложить данную функцию f(x) в ряд по степеням (x-a) и определить интервал сходимости полученного ряда.
, разложить данную функцию f(x) в ряд по степеням (x-a) и определить интервал сходимости полученного ряда.
Задача3. Разлагая подынтегральную функцию в ряд, вычислить приближённое значение данного определённого интеграла с погрешностью δ, не превышающей 0,001.
Задача 4. Найти первые 4-5 членов разложения в ряд Тейлора частного
решения данного дифференциального уравнения при указанных начальных условиях.
Задача 5. Найти решение данного линейного дифференциального неоднородного уравнения второго порядка в виде ряда по степеням x (методом неопределённых коэффициентов). Исследовать структуру полученного общего решения, выделив в нём общее решение соответствующего однородного уравнения, его фундаментальную систему решений и частное решение неоднородного уравнения. Найти частное решение  ,удовлетворяющее начальным условиям
,удовлетворяющее начальным условиям 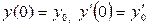 , вычислить значение этого частного решения в точке
, вычислить значение этого частного решения в точке  (
( ) с точностью до 0,01.
) с точностью до 0,01.
Таблица 1.
| N | Задача 1 | Задача 2 | Задача 3 | ||
| f(x) | a | ||||

| 
| 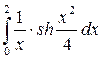
| |||

| 
| 
| |||

| 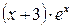
| -2 | 
| ||
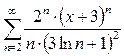
| 
| 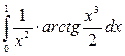
| |||

| 
| -1 | 
| ||

| 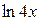
| 
| |||

| 
| 
| 
| ||

| 
| -3 | 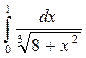
| ||

| 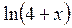
| 
| |||

| 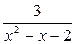
| -2 | 
| ||

| 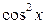
| 
| 
| ||

| 
| 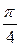
| 
| ||

| 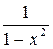
| 
| |||

| 
| -1 | 
| ||
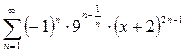
| 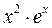
| 
| |||
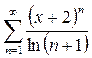
| 
| -1 | 
| ||

| 
| 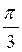
| 
| ||

| 
| 
| |||

| 
| 
| |||

| 
| -1 | 
| ||

| 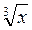
| -8 | 
| ||

| 
| 
| 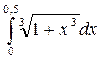
| ||

| 
| -2 | 
| ||

| 
| - 
| 
| ||

| 
| 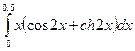
| |||

| 
| 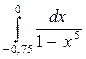
| |||
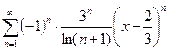
| 
| -1 | 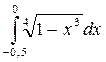
| ||

| 
| 
| |||
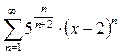
| 
| -2 | 
| ||

| 
| π | 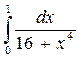
| ||
Таблица 2.
| N | Задача 4 | Задача 5 | |||
| Уравнение | Н. усл. | Уравнение | Н.У. | 
| |
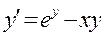
| 
| 
| 
| 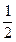
| |
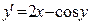
| 
| 
| 
| ||

| 
| 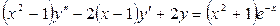
| 
| -1 | |

| 
| 
| 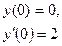
| ||

| 
| 
| 
| ||

| 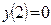
| 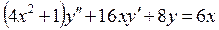
| 
| 
| |
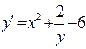
| 
| 
| 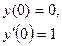
| 
| |

| 
| 
| 
| 
| |
9 
| 
| 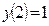
| 
| 
| |

| 
| 
| 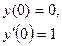
| 
| |
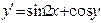
| 
| 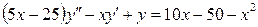
| 
| ||

| 
| 
| 
| ||

| 
| 
| 
| 
| |

| 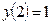
| 
| 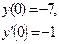
| 
| |

| 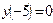
| 
| 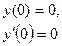
| 
| |
| 
| 
| 
| 
| |

| 
| 
| 
| -1 | |

| 
| 
| 
| ||

| 
| 
| 
| ||

| 
| 
| 
| ||
| 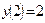
| 
| 
| ||
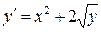
| 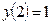
| 
| 
| ||

| 
| 
| 
| ||

| 
| 
| 
| -1 | |

| 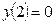
| 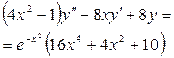
| 
| 
| |

| 
| 
| 
| 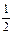
| |

| 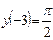
| 
| 
| ||

| 
| 
| 
| 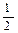
| |

| 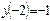
| 
| 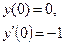
| 
| |

| 
| 
| 
| 
|
Литература.
1.Е.А. Власова. Ряды. Учебник для ВУЗов / под ред. В.С.Зарубина, А.П. Крищенко. – М. Изд-во МГТУ им. Н.Э.Баумана, 2000,-612 с./.
2. Бугров Я.С., Никольский С.М., Высшая математика. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного. – М. «Наука». 1985, 448с..
3. Осипова М.З. «Ряды и их приложения», М., Ротапринт МВТУ,1973.
Оглавление.
Часть 1. Функциональные ряды. 4
Часть 2. Степенные ряды. 7
Часть 3. Разложение функций в степенные ряды. 16
Часть 4. Приближённые вычисления интегралов с помощью рядов. 28
Часть 5. Решение дифференциальных уравнений с помощью рядов. 32
Содержание задания «Степенные ряды». 40
Литература. 47.






