Определение. Степенной ряд - это функциональный ряд вида
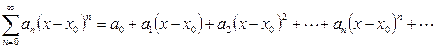, (2.1) где 
- постоянные, называемые коэффициентами степенного ряда.
Теорема Абеля. Если степенной ряд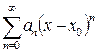 
сходится в некоторой точке 
, то он сходится абсолютно для всех x, таких, что 
. Если степенной ряд расходится в точке 
, то он расходится при любом x, для которого 
.
Следствие. Каждому степенному ряду 
соответствует действительное число 
, или символ + ∞, называемое радиусом сходимости. При этом внутри интервала 
степенной ряд сходится абсолютно, вне данного интервала ряд расходится, поведение в граничных точках каждый раз требует отдельного исследования.
Если R= + ∞, то степенной ряд сходится абсолютно на всей числовой оси. Радиус сходимости числового ряда связан с его коэффициентами формулами Коши-Адамара: 
, или 
. Данные формулы получаются непосредственно в результате применения к ряду 
достаточных признаков сходимости Коши - радикального или Даламбера.
План нахождения области сходимости степенного ряда.
При конкретном значении x числовой ряд, получающийся из степенного, может оказаться знакопеременным. Учитывая это, исследуем ряд, как числовой, считая x фиксированным, сначала на абсолютную сходимость.
1. Применим к ряду из модулей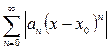 
достаточный признак Даламбера или Коши – радикальный (проверку необходимого признака можно пропустить): 
,
или: 
.
2. Решая это неравенство, определим интервал абсолютной сходимости 
, или,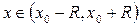 
.
Вне полученного интервала не выполняется необходимый признак сходимости, следовательно, здесь ряд расходится.
3. Чтобы выяснить поведение ряда в граничных точках, подставим в исходный ряд по очереди значения 
, 
и исследуем получившиеся числовые ряды.
В следующих примерах найти области сходимости рядов:
Пример 2.1. 
.
1. Составим ряд из модулей: 
и применим к нему признак Коши – радикальный:
.
Так как для сходимости по признаку Коши необходимо выполнение неравенства 
, требуем: 
.
Откуда получаем: 
.
Итак, 
- интервал абсолютной сходимости ряда.
Выясним поведение ряда в граничных точках интервала сходимости.
2. Подставляем 
в исходный ряд:
Получили знакоположительный ряд. Проверим выполнение необходимого признака сходимости: 
.
Необходимый признак не выполнен – ряд в точке 
расходится.
3. Подставляем 
в исходный ряд: 
.
Получили знакочередующийся ряд. Так как
, ряд в точке 
тоже расходится.
Ответ: интервал абсолютной сходимости ряда 
.
Пример 2.2.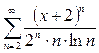 
.
1. Составим ряд из модулей и применим к нему признак Даламбера:
.
Итак, интервал 
- область абсолютной сходимости степенного ряда.
Исследуем поведение ряда в граничных точках.
2. Подставим 
в ряд: 
.
Получили знакочередующийся ряд. Составим ряд из модулей: 
. Необходимый признак выполнен: 
.
Применим к ряду из модулей интегральный признак: 
интеграл расходится, ряд из модулей расходится. Т. к. 
монотонно убывает при увеличении номера n, ряд условно сходится в точке 
по признаку Лейбница.
3. Подставим 
в ряд: 
.
Получили знакоположительный расходящийся ряд (см. пункт 2).
Ответ: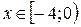 
область сходимости ряда. Интервал 
- область абсолютной сходимости, в точке 
ряд сходится условно.
Пример 2.3. 
.
1. Составим ряд из модулей и применим к нему признак Коши:
.
Область абсолютной сходимости ряда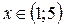 
.
Исследуем поведение ряда в граничных точках области сходимости.
2. Подставим 
в ряд: 
.
Получили знакопеременный ряд. Исследуем ряд из модулей: 
.
Необходимый признак выполнен: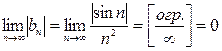 
.
Далее применим признак сравнения: 
.
Все члены ряда из модулей не превосходят членов сходящегося ряда Дирихле 
, следовательно, ряд 
сходится абсолютно.
Значит, ряд 
сходится абсолютно в точке 
.
3. Подставим 
в ряд: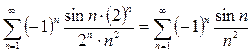 
.
В точке 
степенной ряд сходится абсолютно (см. пункт 2).
Ответ: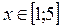 
- область абсолютной сходимости данного ряда.
Пример 2.4.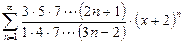 
1. Составим ряд из модулей и исследуем его по признаку Даламбера:
; 
;
- область абсолютной сходимости ряда. Исследуем поведение ряда в граничных точках интервала сходимости. Подставим 
в ряд: 
- знакочередующийся ряд. Проверить выполнение необходимого признака в данном случае достаточно трудно. Заметим, что
Очевидно, что 
, а это значит, что каждый последующий член ряда больше предыдущего, то есть не выполняется необходимый признак сходимости – ряд расходится.
3. В точке 
получим расходящийся ряд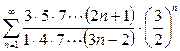 
. Ответ: 
- область абсолютной сходимости ряда.
