Возможность почленного дифференцирования и интегрирования степенного ряда внутри его интервала сходимости, а также простота степенной функции, делают степенные ряды незаменимыми в теоретических и практических исследованиях. Встаёт вопрос о разложении функции в степенной ряд и нахождении области его сходимости.
Теорема. Функция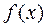 
, бесконечно дифференцируемая в некотором интервале 
, может быть разложена в этом интервале в сходящийся к ней степенной ряд Тейлора 
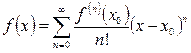, (3.1)
если в этом интервале выполняется условие 
, где
-остаточный член формулы Тейлора, 
. При 
получаем ряд Маклорена: 
.(3.2)
Замечание. Если в некотором интервале, содержащем точку 
, при любом n выполняется неравенство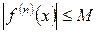 
, М>0,то , и 
разложима в ряд Тейлора.
(Если последнее условие не выполняется, то формально построенный ряд Тейлора может быть сходящимся, но к другой функции.)
Пример 3.1. Можно ли разложить: а) 
в ряд Маклорена;
б) 
в ряд Тейлора по степеням 
;
в)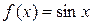 
в ряд Маклорена?
Решение. а) нельзя разложить в ряд Маклорена, так как в точке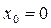 
ни функция, ни её производные не определены; б) 
разложить по степеням нельзя, так как в точке 
функция определена, но является граничной точкой области определения, и производные в ней не определены;
в)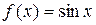 
можно разложить в ряд Маклорена, так как в точке 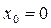определена как сама функция, так и её производная любого порядка.
Притом очевидно, что 
, то есть полученный ряд будет сходиться именно к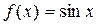 
.
Приёмы разложения функций в степенные ряды.
I. Непосредственное разложение функции в ряд Тейлора.
В этом случае, находя все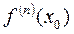 
, формально составляют ряд
и находят область сходимости этого ряда.
Пример 3.2. Разложить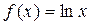 
в ряд Тейлора по степеням 
.
а) Составим ряд Тейлора в виде 
.
Вычислим производные до n порядка и найдём их значения при 
.
………………. ………………………
Подставим вычисленные производные в ряд Тейлора:
.
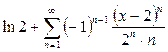б) Область сходимости полученного ряда: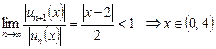 
.
На концах интервала: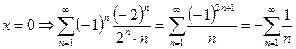 
- расходится, как гармонический ряд. 
- сходится условно.
Итак, область сходимости полученного ряда 
.
в) Чтобы ответить на вопрос, сходится ли полученный ряд именно к функции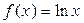 
, проверим выполнимость условия 
.
, 
, 
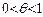.Следовательно, ряд 
в области 
сходится к функции 
, т. е. является разложением данной функции по степеням 
.
Отметим, что непосредственное разложение функций в ряд Тейлора не всегда позволяет получить разложение вида 
,
так как найти общую формулу 
бывает затруднительно. В таких случаях либо ограничиваются конечным числом членов степенного ряда, либо пользуются разложениями в степенной ряд элементарных функций.
