До типових моделей подання знань відносяться логічна, продукційна, фреймова й модель семантичної мережі.
Кожній моделі відповідає своя мова подання знань. Однак на практиці рідко вдається обійтися рамками однієї моделі при розробці ШІС за винятком найпростіших випадків, тому подання знань виходить складним. Крім комбінованого подання за допомогою різних моделей, звичайно використовуються спеціальні засоби, що дозволяють відбити особливості конкретних знань про предметну область, а також різні способи усунення й обліку нечіткості й неповноти знань.
Логічна модель заснована на системі вирахування предикатів першого порядку. Знайомство з логікою предикатів почнемо з вирахування висловлень.
Висловленням називається речення, зміст якого можна виразити значеннями: істина (Т) або неправда (F). Наприклад, речення «лебідь білий» і «лебідь чорний» будуть висловленнями. Із простих висловлень можна скласти більш складні:
«лебідь білий або лебідь чорний»,
«лебідь білий і лебідь чорний»,
«якщо лебідь не білий, то лебідь чорний».
У свою чергу, складні висловлення можна розділити на часткові, які зв'язані між собою за допомогою слів: і, або, не, якщо - то. Елементарними називаються висловлення, які не можна розділити на частині. Логіка висловлень оперує логічними зв'язками між висловленнями, не вона вирішує питання типу: «чи можна на основі висловлення А одержати висловлення В?»; «чи істинно В при істинності А?» і т.п. При цьому семантика висловлень не має значення. Елементарні висловлення розглядаються як змінні логічного типу, над якими дозволені наступні логічні операції:
| заперечення (унарна операція); | |
| ^ | кон'юнкція (логічне множення); |
| v | диз'юнкція (логічне додавання); |
| -> | імплікація (якщо — то); |
| <-> | еквівалентність. |
Вирахування висловлень дозволяє формалізувати лише малу частину безлічі міркувань, оскільки цей апарат не дозволяє враховувати внутрішню структуру висловлення, що існує в природних мовах. Розглянемо приклад міркування про Сократа, що став, класичним;
Р: «Всі люди смертні»; Q: «Сократ - людина»; R: «Сократ - смертний»;
Використовуючи для позначення висловлень логічні змінні Р, Q, R, можна скласти формулу: (P^Q)->R, що може бути інтерпретовано як «Якщо всі люди смертні й Сократ є людиною, то Сократ є смертним». Однак ця формула не є загальновизначною, оскільки відноситься тільки до одного об'єкта (Сократа). Крім того, висловлення R не виводиться з Р и Q, тобто, якби ми не сформулювали R заздалегідь, ми не змогли б записати наведену вище формулу.
Щоб здійснити цей примітивний логічний висновок, висловлення Q варто розділити на дві частини: «Сократ» (суб'єкт) і «людина» (властивість суб'єкта) і представити у вигляді відносини «суб'єкт - властивість», які можна записати за допомогою функції людина (Сократ);
Очевидно, що властивість конкретного суб'єкта з ім'ям «Сократ» бути «людиною» може бути властиво й ряду інших суб'єктів, що дозволяє замінити константу «Сократ» на деяку змінну, наприклад X. Тоді одержимо запис людина (X), що має внутрішню структуру, тобто значення такого висловлення буде залежати від його компонентів. Записана функція вже не є елементарним висловленням, вона називається предикатом. Приклад предиката: «Р більше Q»
Продукційна модель у силу своєї простоти одержала найбільш широке поширення. У цій моделі знання представляються у вигляді сукупності правил типу «ЯКЩО - ТО». Системи обробки знань, що використовують таке подання, одержали назву продукційних систем. До складу експертної системи продукційного типу входять база правил, база фактичних даних (робоча пам'ять) і інтерпретатор правил, що реалізує певний механізм логічного висновку. Будь-яке продукційне правило, що тримається в БЗ, складається із двох частин: антецедента й консеквента.
Антецедент являє собою посилку правила (умовну частину) і складається з елементарних пропозицій, з'єднаних логічними зв'язками І, АБО.
Консеквент (висновок) включає одне або кілька пропозицій, які виражають або деякий факт, або вказівку на певну дію, предмет виконання. Приклади продукційних правил:
ЯКЩО «двигун не заводиться» І «стартер двигуна не працює», ТО «неполадки в системі електроживлення стартера»;
ЯКЩО «тварина має пір'я», ТО «тварина - птах».
Антецеденти й консеквенти правил формуються з атрибутів і значень, наприклад:
| Атрибут | Значення |
| Двигун | Не заводиться |
| Стартер двигуна | Не працює |
| Тварина | Має пір'я |
| Тварина | Птах |
Існують два типи продукційних систем - із прямими й зворотними висновками. Прямі висновки реалізують стратегію «від фактів до висновків». При зворотних висновках висуваються гіпотези ймовірних висновків, які можуть бути підтверджені або спростовані на підставі фактів, що надходять у робочу пам'ять. Існують також системи із двоспрямованими висновками.
Основні переваги продукційних систем пов'язані із простотою подання знань і організації логічного висновку. До недоліків систем продукцій можна віднести наступні:
- відмінність від структур знань, властивих людині;
- неясність взаємовідносин правил;
- складність оцінки цілісного образа знань;
- низька ефективність обробки знань.
При розробці невеликих систем (десятки правил) проявляються в основному позитивні сторони систем продукцій, однак при збільшенні обсягу знань більше помітними стають слабкі сторони.
Фреймова модель подання знань засноване на теорії фреймів М. Мінського, котра являє собою систематизовану психологічну модель пам'яті людини і його свідомості. Ця теорія має досить абстрактний характер, тому тільки на її основі неможливе створення конкретних мов подання знань.
Фреймом називається структура даних для подання деякого концептуального об'єкта.
Фрейм має ім'я, що служить для ідентифікації описуваного їм поняття, і містить ряд описів — слотів, за допомогою яких визначаються основні структурні елементи цього поняття. За слотами випливають шпації, у які поміщають дані, що представляють поточні значення слотів. Слот може містити не тільки конкретне значення, але також ім'я процедури, що дозволяє обчислити це значення по заданому алгоритму. Наприклад, слот з ім'ям вік може містити ім'я процедури, що обчислює вік людини по даті народження, записаної в іншому слоті, і поточній даті. Процедури, що розташовуються у слотах, називаються зв'язаними або приєднаними процедурами. Виклик зв'язаної процедури здійснюється при звертанні до слоту, у якому вона поміщена. Заповнювачами слота можуть бути також правила продукций, які використовуються для визначення конкретного значення. У слоті може утримуватись не одне, а кілька значень, тобто в якості структурних складових фреймів можуть використовуватись дані складних типів, а саме: масиви, списки, безлічі, фрейми й т.д. Наприклад, у слоті з ім'ям брат може втримуватись перелік імен, якщо об'єкт, описуваний даним фреймом, має декількох братів. Значення слота може являти собою деякий діапазон або перелік можливих значень, арифметичне вираження, фрагмент тексту й т.д.
Сукупність даних предметної області може бути представлена безліччю взаємозалежних фреймів, що утворюють єдину фреймову систему, у якій поєднуються декларативні й процедурні знання. Така система має як правило, ієрархічну структуру, у якій фрейми з'єднані один з одним за допомогою родовидових зв'язків. На верхньому рівні ієрархії перебуває фрейм, що містить найбільш загальну інформацію, істинною для всіх інших фреймів. Фрейми мають здатність успадковувати значення характеристик своїх батьків. Наприклад, фрейм АФРИКАНСЬКИЙ_СЛОН успадковує від фрейму СЛОН значення характеристики колір=«сірий». Значення характеристики в дочірньому фреймі може відрізнятися від батьківського, наприклад, значенням даного слота для фрейму АЗІАТСЬКИЙ_СЛОН є колір=«коричневий».
Над фреймами можна робити деякі теоретико-множинні операції, наприклад об'єднання й перетинання. При об'єднанні фреймів у результуючому фреймі будуть присутні всі слоти, які зустрічалися у вихідних фреймах. У слотах, що не є загальними, будуть збережені вихідні значення. Якщо в поєднуваних фреймах були однойменні слоти, у результуючому фреймі залишиться один слот з таким ім'ям, значення його визначиться в результаті об'єднання значень однойменних слотів. При перетинанні фреймів у результуючому фреймі будуть присутні тільки ті слоти, які були у всіх вихідних фреймах. Обчислити результуючі значення можна двома способами. Перший спосіб полягає в тому, що в результуючому фреймі присутні тільки ті значення, які збігалися у вихідних фреймах. У другому способі результуючі значення знаходять шляхом перетинання значень із вихідних фреймів.
Фреймові системи поділяються на статичні й динамічні, останні допускають зміну фреймів у процесі рішення завдання.
Наприклад
| Фрейм КЕРІВНИК | ||
| Ім'я слота | Значення слота | Тип значення слота |
| Ім'я | Іванов И. И. | Рядок символів |
| Породжений | 01.01.1965 | Дата |
| Вік | age(dama, породжений) | Процедура |
| Спеціальність | Юрист | Рядок символів |
| Відділ | Відділ кадрів | Рядок символів |
| Зарплата | Число | |
| Адреса | БУДИНОК_АДРЕС | Фрейм |
У загальному випадку структура даних фрейму може містити більш широкий набір інформації, у який входять наступні атрибути.
Ім'я фрейму. Воно служить для ідентифікації фрейму в системі й повинно бути унікальним. Фрейм являє собою сукупність слотів, число яких може бути довільним. Число слотів у кожному фреймі встановлюється проектувальником системи, при цьому частина слотів визначається самою системою для виконання специфічних функцій (системні слоти), прикладами яких є: слот-покажчик батька даного фрейму (IS-А), слот-покажчик дочірніх фреймів, слот для уведення ім'я користувача, слот для уведення дати визначення фрейму, слот для уведення дати зміни фрейму й т.д.
Ім'я слота. Воно повинно бути унікальним у межах фрейму. Звичайне ім'я слота являє собою ідентифікатор, що наділений певною семантикою. Як ім'я слота може виступати довільний текст. Наприклад, <Ім'я слота> = Головний герой роману Ф. М. Достоєвського «Ідіот», <3начення слота> = Князь Мишкін. Імена системних слотів звичайно зарезервовані, у різних системах вони можуть мати різні значення. Системні слоти служать для редагування бази знань і керування висновком у фреймовій системі.
Покажчики спадкування. Вони показують, яку інформацію про атрибути слотів із фрейму верхнього рівня успадковують слоти з аналогічними іменами в даному фреймі. Покажчики спадкування характерні для фреймових систем ієрархічного типу, заснованих на відносинах типу «абстрактне - конкретне». У конкретних системах покажчики спадкування можуть бути організовані різними способами, і мати різні позначення:
U (Unique) - значення слота не успадковується;
S (Same) - значення слота успадковується;
R (Range) - значення слота повинні перебувати в межах інтервалу значень, зазначених в однойменному слоті батьківського фрейму;
О (Override) - при відсутності значення в поточному слоті воно успадковується із фрейму верхнього рівня, однак у випадку визначення значення поточного слота воно може бути унікальним. Цей тип покажчика виконує одночасно функції покажчиків U і S.
Покажчик типу даних. Він показує тип значення слота. Найбільш вживані типи: frame - покажчик на фрейм; real - речовинне число; integer - ціле число; boolean - логічний тип; text - фрагмент тексту; list - список; table - таблиця; expression - вираження; lisp - зв'язана процедура й т.д.
Значення слота. Воно повинне відповідати зазначеному типу даних і умові спадкування.
Демони. Демоном називається процедура, що запускається автоматично при виконанні деякої умови. Демони автоматично запускаються при звертанні до відповідного слоту. Типи демонів пов'язані з умовою запуску процедури. Демон з умовою IF-NEEDED запускається, якщо в момент звертання до слоту його значення не було встановлено. Демон типу IF-ADDED запускається при спробі зміни значення слота. Демон IF-REMOVED запускається при спробі видалення значення слота. Можливі також інші типи демонів. Демон є різновидом зв'язаної процедури.
Зв ' язна процедура. У якості слота може використовуватись процедура, яка називається службовою в мові або методом у мовах об’єктно-орієнтованого програмування. Приєднана процедура запускається за повідомленням, переданим з іншого фрейму. Демони й приєднані процедури є процедурними знаннями, об'єднаними разом з декларативними в єдину систему. Ці процедурні знання є засобами керування висновком у фреймових системах, причому з їхньою допомогою можна реалізувати будь-який механізм висновку. Подання таких знань і заповнення ними інтелектуальних систем - досить нелегка справа, що вимагає додаткових витрат праці й часу розробників ШІС. Тому проектування фреймових систем виконується, як правило, фахівцями, що мають високий рівень кваліфікації в області штучного інтелекту.
Приклад мережі фреймів наведений на мал. 5.10

Мал. 5.10 - Мережа фреймів
На ньому поняття УЧЕНЬ успадковує властивості фреймів ДИТИНА й ЛЮДИНА, які перебувають на більш високих рівнях ієрархії. Якщо буде задане питання «чи люблять учні солодке?», то треба відповісти «так», тому що цією властивістю володіють всі діти, що зазначено у фреймі ДИТИНА. Спадкування властивостей може бути частковим, наприклад «вік» для учнів не успадковується із фрейму «дитина», тому, що явно зазначене у власному фреймі.
В останні роки термін «фреймовий» часто заміняють терміном «об’єктно-орієнтований». Шаблон фрейму можна розглядати як клас, екземпляр фрейму - як об'єкт. Мови об’єктно-орієнтованого програмування (ООП) надають засоби створення класів і об'єктів, а також засоби для опису процедур обробки об'єктів (методи). Мови ООП які не містять засобів реалізації приєднаних процедур, не дозволяють організувати гнучкий механізм логічного виводу, тому розроблені на них програми або являють собою об’єктно-орієнтовані бази даних, або вимагають інтеграції з іншими засобами обробки знань (наприклад, з мовою PROLOG).
Існують також спеціалізовані мови подання знань на основі фреймової моделі.
Розрізняють фрейми-зразки, фрейми-екземпляри, фрейми-структури, фрейми-ролі, фрейми-сценарії, фрейми-ситуації. Система пов'язаних фреймів може утворювати семантичну мережу.
Застосовуються фрейми в експертних системах і інших інтелектуальних системах різного призначення.
Зазвичай під поняттям семантична мережа мають на увазі систему знань деякої предметної області, що має певний зміст у вигляді цілісного образа мережі, вузли якої відповідають поняттям і об'єктам, а дуги — відносинам між об'єктами. При побудові семантичної мережі відсутні обмеження на число зв'язків і на складність мережі. Для того щоб формалізація виявилася можливою, семантичну мережу необхідно систематизувати. Семантичні мережі Куілліана систематизують функції відносин між поняттями за допомогою наступних ознак:
- безліч - підмножина (типи відносин «абстрактне - конкретне», «ціле - частина», «рід - вид»);
- індекси (властивості, імена прикметники в мові й т.п.);
- кон'юнктивні зв'язки (логічне І);
- диз'юнктивні зв'язки (логічне АБО);
- зв'язки по ВИКЛЮЧАЮЧОМУ АБО;
- відносини «причина - наслідок» і ін.
При побудові семантичної мережі відсутні обмеження на число елементів і зв'язків. Тому систематизація відносин між об'єктами в мережі необхідна для подальшої формалізації. Приклад семантичної мережі представлений на мал. 5.11.
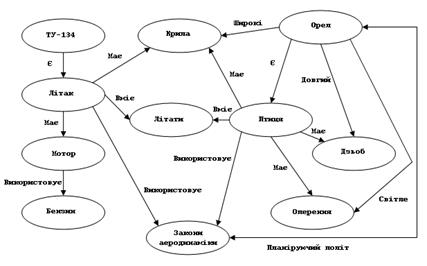
Мал 5.11 - Приклад семантичної мережі
Для реалізації семантичних мереж існують спеціальні мережні мови: NET, мова реалізації систем SIMER+MIR і ін. Широко відомі експертні системи, що використовують семантичні мережі як мову подання знань: PROSPECTOR, CASNET, TORUS.
Систематизація відносин конкретної семантичної мережі залежить від специфіки знань предметної області і є складним завданням. Особливої уваги заслуговують загальнозначущі відносини, що є присутнім у багатьох предметних областях. Саме на таких відносинах заснована концепція семантичної мережі. У семантичних мережах, так само як при фреймовому поданні знань, декларативні й процедурні знання не розділені, отже, база знань не відділена від механізму висновку.
Процедура логічного висновку зазвичай являє сукупність процедур обробки мережі. Семантичні мережі набули широкого застосування в системах розпізнавання мови й експертних системах.






